备战2014高考数学 高频考点归类分析（真题为例）：解高次、分式不等式和指数、对数不等式 3页

高频考点分析 解高次、分式不等式和指数、对数不等式 典型例题：[来源:学科网]‎ 例1. （2012年重庆市理5分）不等式的解集为【 】‎ ‎ A. B. C. D. ‎ ‎【答案】A。‎ ‎【考点】分式不等式的解法。‎ ‎【分析】化分式不等式为整式不等式求解：‎ ‎。故选A。‎ 例2. （2012年重庆市文5分）不等式 的解集是为【 】‎ ‎（A） （B） （C）（-2，1）（D）∪‎ ‎【答案】C。‎ ‎【考点】其他不等式的解法。‎ ‎【分析】利用等价变形直接转化分式不等式为二次不等式求解即可：‎ ‎ 。故选C。‎ 例3. （2012年江西省文5分）不等式的解集是 ▲ 。‎ ‎【答案】。‎ ‎【考点】其它不等式的解法。‎ ‎【解析】不等式可化为，解得。‎ ‎　　　　∴不等式的解集为。[来源:学科网]‎ 例4. （2012年湖南省文5分）不等式的解集为　　▲　　..‎ ‎【答案】。‎ ‎【考点】一元二次不等式的解法。‎ ‎【解析】由，得，从而的不等式x2-5x+6≤0的解集为 ‎。‎ 例5. （2012年山东省文5分）函数的定义域为【 】‎ ‎ A B C D [来源:学科网ZXXK]‎ ‎【答案】B。‎ ‎【考点】函数的定义域。分式、对数、二次根式有意义的条件。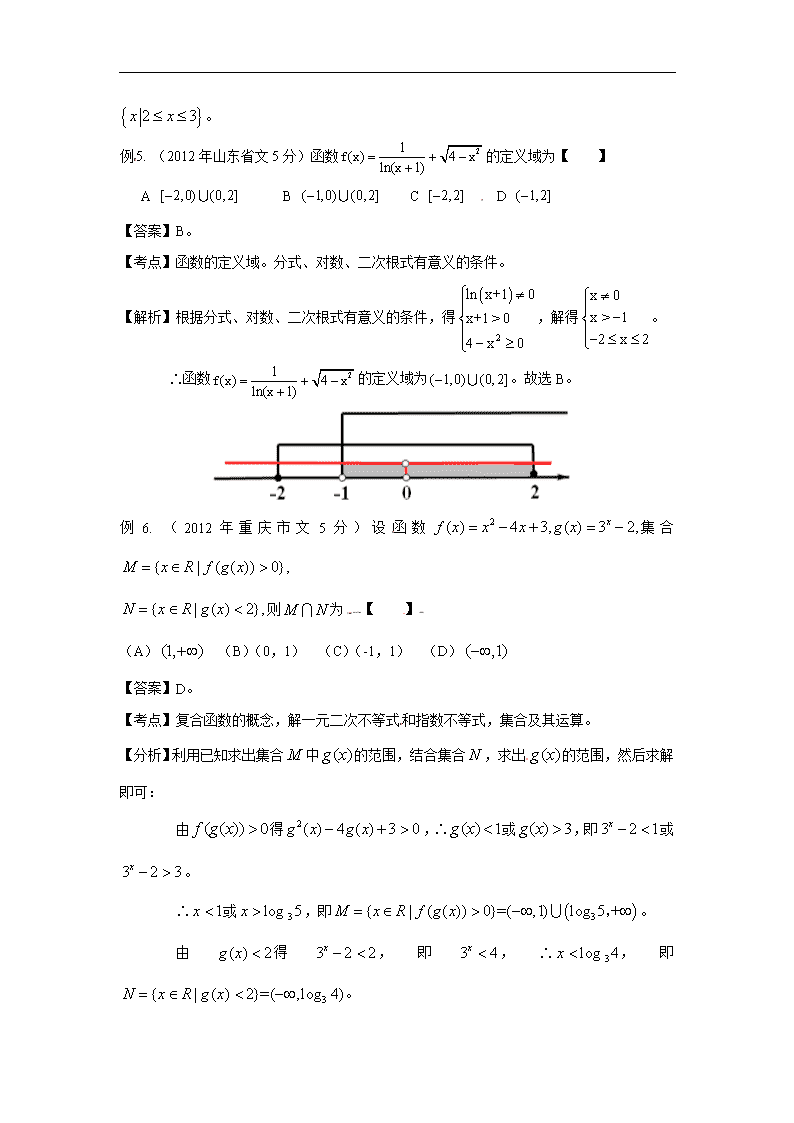‎ ‎【解析】根据分式、对数、二次根式有意义的条件，得，解得。‎ ‎ ∴函数的定义域为。故选B。‎ 例6. （2012年重庆市文5分）设函数集合 ‎ 则为21世纪教【 】育网 ‎（A） （B）（0，1） （C）（-1，1） （D）‎ ‎【答案】D。‎ ‎【考点】复合函数的概念，解一元二次不等式和指数不等式，集合及其运算。‎ ‎【分析】利用已知求出集合中的范围，结合集合，求出的范围，然后求解即可：‎ 由得，∴或，即或。‎ ‎∴或，即。‎ 由得，即，∴，即。‎ ‎∴。故选D。‎ 例7. （2012年上海市理14分）已知函数.‎ ‎ （1）若，求的取值范围；（6分）‎ ‎ （2）若是以2为周期的偶函数，且当时，有，求函数的反函数.（8分）‎ ‎【答案】（1）由，得。[来源:学科网ZXXK]‎ ‎ 由得。‎ ‎ ∵，∴，解得。‎ ‎ 由得，。‎ ‎ （2）当时，，‎ ‎∴。‎ 由单调性可得。[来源:学科网]‎ ‎∵，∴所求反函数是，。‎ ‎【考点】对数函数的概念、性质，反函数的求法。‎ ‎【解析】（1）由，结合对数函数的性质，列不等式组求解即可。‎ ‎（2）根据对数函数与指数函数互为反函数的性质求解。‎