- 57.00 KB
- 2021-04-14 发布
§2.7 函数与方程
一、填空题(本大题共9小题,每小题6分,共54分)
1.(2010·北京东城区期末)在以下区间中,存在函数f(x)=x3+3x-3的零点的是_______
①[-1,0] ②[1,2]
③[0,1] ④[2,3]
2.(2010·镇江联考)方程2-x+x2=3的实数解的个数为________个.
3.函数f(x)=3ax-2a+1在区间[-1,1]上存在一个零点,则a的取值范围是______________.
4.如果函数f(x)=x2+mx+m+2的一个零点是0,则另一个零点是________.
5.(2010·苏州模拟)偶函数f(x)在区间为[0,a](a>0)上是单调函数,且f(0)·f(a)<0,则方程f(x)=0在区间[-a,a]内根的个数是______.
6.函数f(x)=3x-7+ln x的零点位于区间(n,n+1) (n∈N)内,则n=________.
7.已知函数f(x)=x2+(1-k)x-k的一个零点在(2,3)内,则实数k的取值范围是________.
8.(2010·常州模拟)若函数f(x)=x2+ax+b的两个零点是-2和3,则不等式af(-2x)>0的解集是__________.
9.(2010·南京一模)若f(x)= 则函数g(x)=f(x)-x的零点为____________.
二、解答题(本大题共3小题,共46分)
10.(14分)关于x的二次方程x2+(m-1)x+1=0在区间[0,2]上有解,求实数m的取值范围.
11.(16分)已知函数f(x)=4x+m·2x+1有且仅有一个零点,求m的取值范围,并求出该零点.
12.(16分)(1)m为何值时,f(x)=x2+2mx+3m+4.
①有且仅有一个零点;
②有两个零点且均比-1大;
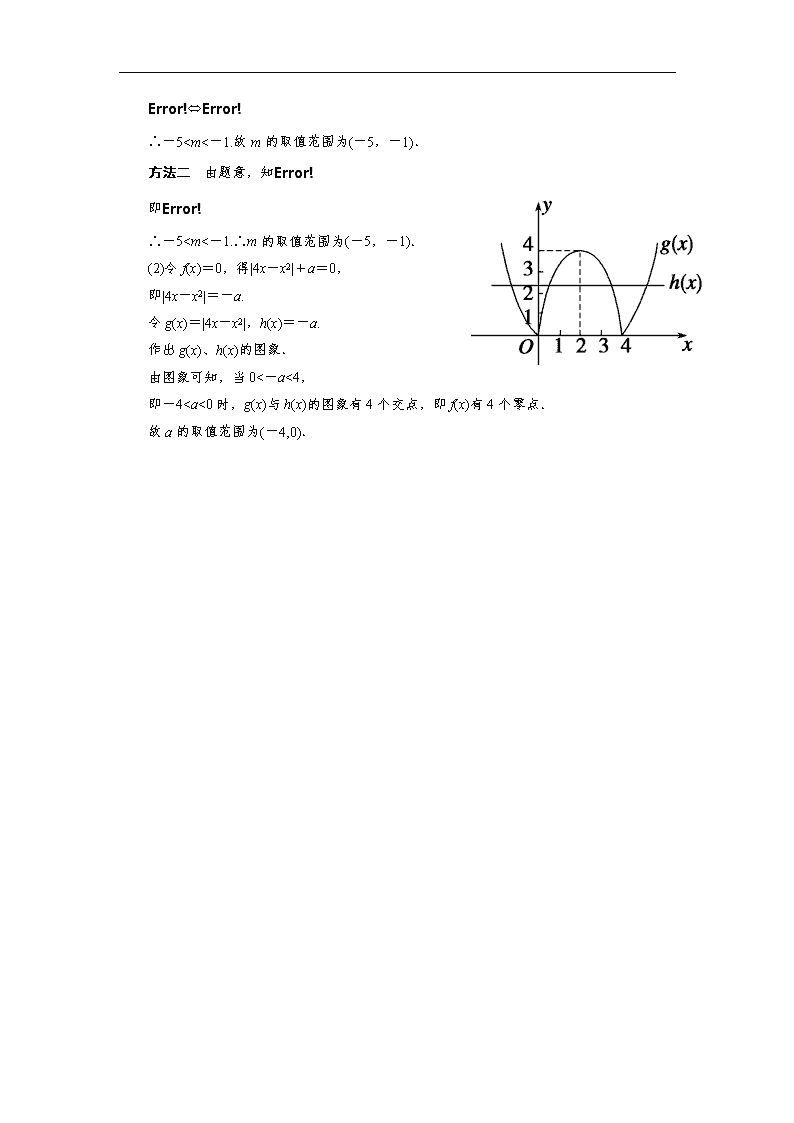
(2)若函数f(x)=|4x-x2|+a有4个零点,求实数a的取值范围.
答案
1.③ 2.2 3.(-∞,-1]∪ 4.2
5.2 6.2 7.(2,3) 8. 9.1+或1
10.解 设f(x)=x2+(m-1)x+1,x∈[0,2],
①若f(x)=0在区间[0,2]上有一解,
∵f(0)=1>0,则应有f(2)≤0,
又∵f(2)=22+(m-1)×2+1,∴m≤-.
②若f(x)=0在区间[0,2]上有两解,则
,∴.
∴,∴-≤m≤-1,
由①②可知m≤-1.
11.解 ∵f(x)=4x+m·2x+1有且仅有一个零点,
即方程(2x)2+m·2x+1=0仅有一个实根.
设2x=t (t>0),则t2+mt+1=0.
当Δ=0时,即m2-4=0,
∴m=-2时,t=1;m=2时,t=-1(不合题意,舍去),
∴2x=1,x=0符合题意.
当Δ>0时,即m>2或m<-2时,
t2+mt+1=0有两正或两负根,
即f(x)有两个零点或没有零点.
∴这种情况不符合题意.
综上可知:m=-2时,f(x)有唯一零点,该零点为x=0.
12.解 (1)①f(x)=x2+2mx+3m+4有且仅有一个零点⇔
方程f(x)=0有两个相等实根⇔Δ=0,
即4m2-4(3m+4)=0,即m2-3m-4=0,∴m=4或m=-1.
②方法一 设f(x)的两个零点分别为x1,x2,
则x1+x2=-2m,x1·x2=3m+4.
由题意,知⇔
⇔
∴-5
相关文档
- 高考数学复习练习试题11_1随机事件2021-04-13 13:40:153页
- 高考数学复习练习试题10_2总体分布2021-04-13 11:48:445页
- 高考数学复习练习试题9_1直线的方2021-04-13 09:13:523页
- 高考数学复习练习第1部分 专题七 2021-04-13 03:12:222页
- 高考数学复习练习试题10_3变量的相2021-04-12 11:22:165页
- 高考数学复习练习试题12_2基本算法2021-02-26 22:07:485页
- 高考数学复习练习试题4_4函数y=Asin2021-02-26 21:56:014页
- 高考数学复习练习试题4_1任意角和2021-02-26 20:48:013页
- 高考数学复习练习第1部分 专题五 2021-02-26 20:46:515页
- 高考数学复习练习试题8_5立体几何2021-02-26 19:46:594页