高考数学复习课时提能演练(四十九) 7_8 13页

‎ ‎ 课时提能演练(四十九)‎ ‎(45分钟 100分)‎ 一、选择题(每小题6分，共36分)‎ ‎1.已知直线l1的方向向量是a=(2,4,x)，直线l2的方向向量是b=(2，y,2)，若|a|=6，且a·b=0，则x+y的值是( )‎ ‎(A)-3或1 (B)3或-1‎ ‎(C)-3 (D)1‎ ‎2.在正方体ABCD-A1B‎1C1D1中，若E为A‎1C1中点，则直线CE垂直于( )‎ ‎(A)AC (B)BD (C)A1D (D)A‎1A ‎3.(2012·三明模拟)如图，正方形ACDE与等腰直角 三角形ACB所在的平面互相垂直，且AC=BC=2，∠ACB ‎=90°，F、G分别是线段AE、BC的中点，则AD与GF 所成的角的余弦值为( )‎ ‎(A) (B) (C) (D)‎ ‎4.(2012·金华模拟)正三棱柱ABC—A1B‎1C1的棱长都为2，‎ E，F，G为AB，AA1，A‎1C1的中点，则B‎1F与平面GEF所 成角的正弦值为( )‎ ‎(A) (B)‎ ‎(C) (D)‎ ‎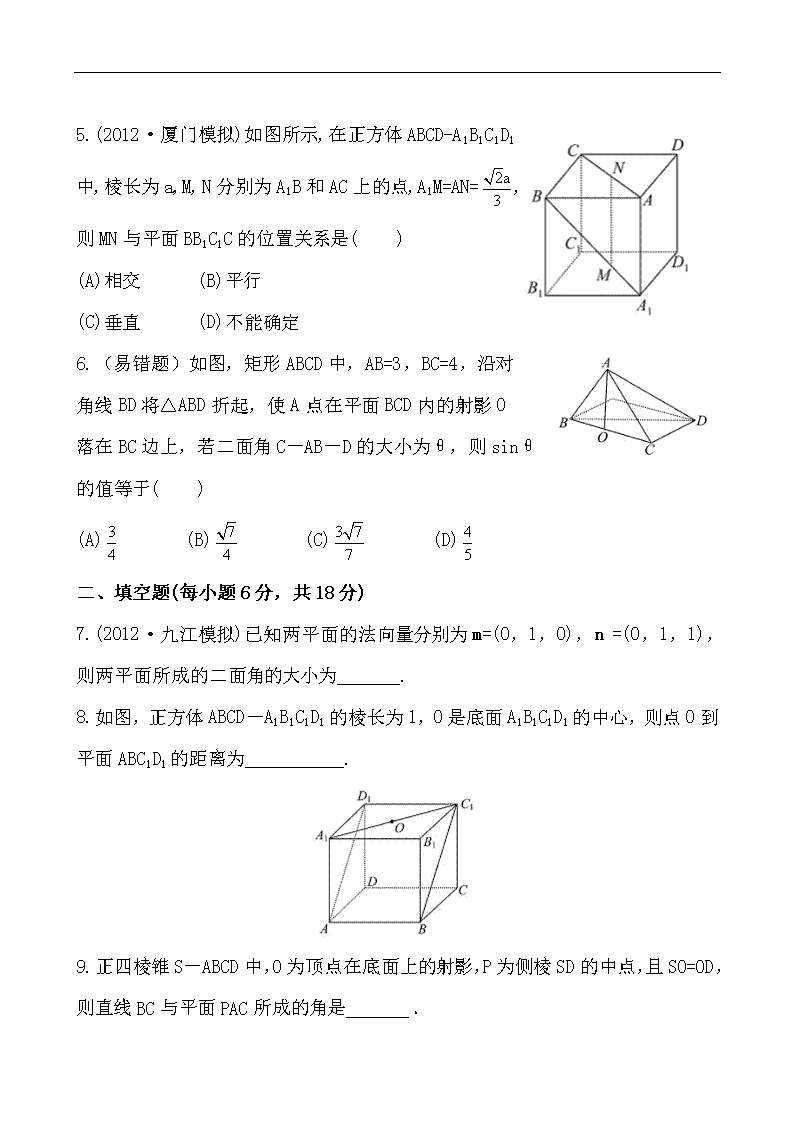5.(2012·厦门模拟)如图所示,在正方体ABCD-A1B‎1C1D1‎ 中,棱长为a,M,N分别为A1B和AC上的点,A‎1M=AN=,‎ 则MN与平面BB‎1C1C的位置关系是( )‎ ‎(A)相交 (B)平行 ‎(C)垂直 (D)不能确定 ‎6.（易错题）如图，矩形ABCD中，AB=3，BC=4，沿对 角线BD将△ABD折起，使A点在平面BCD内的射影O 落在BC边上，若二面角C－AB－D的大小为θ，则sinθ 的值等于( )‎ ‎(A) (B) (C) (D)‎ 二、填空题(每小题6分，共18分)‎ ‎7.(2012·九江模拟)已知两平面的法向量分别为m=(0，1，0)，n =(0，1，1)，则两平面所成的二面角的大小为_______.‎ ‎8.如图，正方体ABCD－A1B‎1C1D1的棱长为1，O是底面A1B‎1C1D1的中心，则点O到平面ABC1D1的距离为___________.‎ ‎9.正四棱锥S－ABCD中，O为顶点在底面上的射影，P为侧棱SD的中点，且SO=OD，则直线BC与平面PAC所成的角是_______．‎ 三、解答题(每小题15分，共30分)‎ ‎10.(预测题)如图，已知四棱锥P—ABCD的底面 是正方形，PA⊥底面ABCD，且PA=AD=2，点M、N分别在 侧棱PD、PC上，且PM=MD.‎ ‎(1)求证：AM⊥平面PCD；‎ ‎(2)若，求平面AMN与平面PAB所成二面角的余弦值.‎ ‎11.（2012·厦门模拟)如图，在三棱锥P－ABC中， ‎ PA⊥底面ABC，PA=AB,∠ABC=60°,∠BCA=90°,点 D、E分别在棱PB，PC上，且DE∥BC.‎ ‎（1）求证：BC⊥平面PAC；‎ ‎（2）当D为PB的中点时，求AD与平面PAC所成角的余弦值.‎ ‎【探究创新】‎ ‎(16分)如图，在矩形ABCD中，AB=2，BC=a，△PAD为等边三角形，又平面PAD⊥平面ABCD．‎ ‎(1)若在边BC上存在一点Q，使PQ⊥QD，求a的取值范围；‎ ‎(2)当边BC上存在唯一点Q，使PQ⊥QD时，求二面角A－PD－Q的余弦值．‎ 答案解析 ‎1.【解析】选A.由题意知,‎ 得x=±4.‎ 由·=4+4y+2x=0得x=-2y-2,‎ 当x=4时，y=-3,∴x+y=1；‎ 当x=-4时，y=1,∴x+y=-3,‎ 综上x+y=-3或1.‎ ‎2.【解题指南】合理建立坐标系，分别求出选项中的线段对应的向量，即可求得结果.‎ ‎【解析】选B.以A为原点，AB、AD、AA1所在直线分别为x，y，z轴建立空间直角坐标系，‎ 设正方体棱长为1，‎ 则A(0，0，0)，C(1，1，0)，B(1，0，0)，‎ D(0，1，0)，A1(0，0，1)，E(，，1)，‎ ‎∴=(，，1)，‎ ‎=(1，1，0)，=(-1，1，0)，‎ ‎=(0，1，-1)，=(0，0，-1)，‎ 显然，∴，即CE⊥BD.‎ ‎3.【解析】选A.如图，正方形ACDE与等腰直角三角形ACB所在的平面互相垂直，且AC=BC=2，∠ACB=90°，F、G分别是线段AE、BC的中点.‎ 以C为原点建立空间直角坐标系Cxyz,‎ A(0，2，0)，B(2，0，0)，D(0，0，2)，G(1，0，0)，F(0，2，1)，‎ ‎=(0，-2，2)，=(-1，2，1)，‎ ‎∴，=-2，‎ ‎∴.‎ ‎∴直线AD与GF所成角的余弦值为.‎ ‎【误区警示】本题容易忽视异面直线所成角的范围而误选B.‎ ‎【变式备选】在正方体ABCD－A1B‎1C1D1中，M为DD1的中点，O为底面ABCD的中心，P为棱A1B1上任意一点，则直线OP与直线AM所成的角是( )‎ ‎(A) (B) (C) (D)‎ ‎【解析】选D.建立坐标系，通过向量的坐标运算可知AM⊥OP总成立，即AM与OP所成的角为．‎ ‎4.【解析】选A.如图，取A1B1的中点E1，建立如图所示空间直角坐标系Exyz.‎ 则E(0,0,0),F(-1,0,1),B1(1,0,2),A1(-1,0,2),‎ C1(0,,2),G().‎ ‎∴=(-2,0,-1),‎ 设平面GEF的一个法向量为n=(x,y,z),‎ 由，得，‎ 令x=1,则=(1,,1),‎ 设B‎1F与平面GEF所成角为θ，则 ‎.‎ ‎5.【解题指南】建立坐标系，判断与平面BB‎1C1C的法向量的关系.‎ ‎【解析】选B.分别以C1B1，C1D1，C‎1C所在直线为x,y,z轴，建立空间直角坐标系.‎ ‎∵A‎1M=AN=,‎ ‎∴M(),N().∴.‎ 又C1(0，0，0)，D1(0,a,0),∴=(0,a,0).‎ ‎∴.∴.‎ ‎∵是平面BB‎1C1C的一个法向量，‎ 且MN平面BB‎1C1C，‎ ‎∴MN∥平面BB‎1C1C.‎ ‎6.【解析】选A.由题意可求得BO=，OC=，AO=，‎ 建立空间直角坐标系如图，则 C(,0,0)，B(,0,0)，A(0,0,)，D(,3,0)，‎ ‎=(4,3,0)，=()‎ 设=(x，y，z)是平面ABD的一个法向量．‎ 则，取z=，x=7,y=.‎ 则.‎ 又=(0,3,0)是平面ABC的一个法向量．‎ ‎∴.‎ sinθ.‎ ‎【方法技巧】求二面角的策略 ‎(1)法向量法，其步骤是：①建系，②分别求构成二面角的两个半平面的法向量，③求法向量夹角的余弦值，④根据题意确定二面角的余弦值或其大小.‎ ‎(2)平面角法，该法就是首先利用二面角的定义，找出二面角的平面角，然后用向量法或解三角形法求其余弦值.‎ ‎7.【解析】，∴,‎ ‎∴两平面所成二面角的大小为或.‎ 答案：或 ‎【误区警示】本题容易认为两平面所成角只有,而忽视.‎ ‎8.【解析】以D为原点，DA、DC、DD1为x轴、y轴、z轴建立空间直角坐标系，则A(1,0,0)，B(1,1,0)，D1(0,0,1)，C1(0,1,1)，O(,,1)，设平面ABC1D1的法向量=(x,y,z)，‎ 由，‎ 得，‎ 令x=1，得n=(1,0,1)，‎ 又，‎ ‎∴O到平面ABC1D1的距离.‎ 答案: ‎ ‎9.【解析】如图，以O为原点建立空间直角坐标系Oxyz.‎ 设OD=SO=OA=OB=OC=a，则A(a,0,0)，B(0，a,0)，C(-a,0,0)，‎ P(0,,)，‎ 则=(‎2a,0,0)，=(-a,,)，‎ ‎=(a，a,0)，‎ 设平面PAC的一个法向量为，可取=(0,1,1)，‎ 则，‎ ‎∴=60°，‎ ‎∴直线BC与平面PAC所成的角为90°－60°=30°.‎ 答案：30°‎ ‎10.【解析】(1)∵PA⊥底面ABCD，CD⊂底面ABCD，‎ ‎∴PA⊥CD.又∵正方形ABCD中，CD⊥AD，PA∩AD=A,∴CD⊥平面PAD，‎ 而AM⊂平面PAD，∴CD⊥AM.由题意知AM⊥PD,‎ 又PD∩CD=D，∴AM⊥平面PCD.‎ ‎(2)如图建立空间直角坐标系Axyz,‎ 又PA=AD=2，‎ 则有P(0，0，2)，D(0，2，0)，M(0，1，1)，C(2，2，0)，∴=(2,2,-2),‎ 设N(x,y,z),∵,则有x-0=(2-x),∴.‎ 同理可得,∴N().‎ 由，得PC⊥AN.‎ 又AM⊥平面PCD,∴AM⊥PC.AM∩AN=A,‎ ‎∴PC⊥平面AMN，‎ ‎∴平面AMN的一个法向量为=(2，2，-2)，‎ 而平面PAB的法向量可为=(0，2，0)，‎ ‎∴.‎ 故所求平面AMN与平面PAB所成二面角的余弦值为.‎ ‎【变式备选】(2012·吉林模拟)如图,已知四棱锥 P-ABCD的底面ABCD是边长为2的正方形，PD⊥底 面ABCD，E、F分别为棱BC、AD的中点.‎ ‎(1)若PD=1，求异面直线PB与DE所成角的余弦值.‎ ‎(2)若二面角P-BF-C的余弦值为，求四棱锥P-ABCD的体积.‎ ‎【解析】(1)E，F分别为棱BC，AD的中点，ABCD是边长为2的正方形⇒DF∥BE且DF=BE⇒DFBE为平行四边形⇒DE∥BF⇒∠PBF等于PB与DE所成的角.‎ ‎△PBF中，BF=，PF=，PB=3⇒cos∠PBF=⇒异面直线PB和DE所成角的余弦值为.‎ ‎(2)以D为原点，直线DA，DC，DP分别为x,y,z轴建立空间直角坐标系，设PD=a，可得如下点的坐标：P(0,0,a)，F(1，0，0)，B(2，2，0)，则有：=(1，0，-a)，=(1，2，0)，‎ 因为PD⊥底面ABCD，所以平面ABCD的一个法向量为=(0，0，1)，‎ 设平面PFB的一个法向量为=(x,y,z)，则可得即，‎ 令x=1，得，，所以.已知二面角P-BF-C的余弦值为，所以得：，解得a=2.‎ 因为PD是四棱锥P-ABCD的高，所以，其体积为VP-ABCD=×2×4=.‎ ‎11.【解析】以A为原点建立空间直角坐标系 ‎ A－xyz,设PA＝a,由已知可得A（0，0，0），‎ B（）,‎ C().‎ ‎（2）∵D为PB的中点，DE∥BC,∴E为PC的中点，‎ ‎∴又由（1）知，BC⊥平面PAC,‎ ‎∴DE⊥平面PAC，垂足为点E.‎ ‎∴∠DAE是AD与平面PAC所成的角，‎ ‎【探究创新】‎ ‎【解析】(1)取AD中点O，连接PO，则PO⊥AD ‎∵平面PAD⊥平面ABCD，‎ 平面PAD∩平面ABCD=AD，‎ ‎∴PO⊥平面ABCD.建立如图的空间直角坐标系，‎ 则P(0,0,),D(,0,0)．‎ 设Q(t，2，0)，‎ 则．‎ ‎∵PQ⊥QD，∴．‎ ‎∴a=2(t+)，∵a>0,∴t>0,∴2(t+)≥8,等号成立当且仅当t=2．‎ 故a的取值范围为［8,+∞)． ‎ ‎(2)由(1)知，当t=2,a=8时，边BC上存在唯一点Q，使PQ⊥QD．‎ 此时Q(2，2，0)，D(4，0，0),P(0,0,4)．‎ 设=(x,y,z)是平面PQD的法向量，‎ ‎=(2,2,)，=(-2,2,0).‎ 由 得 令x=y=3，则=(3,3,)是平面PQD的一个法向量．‎ 而=(0,2,0)是平面PAD的一个法向量，‎ 设二面角A－PD－Q为θ，‎ 由．‎ ‎∴二面角A－PD－Q的余弦值为．‎