- 137.00 KB
- 2021-04-12 发布
B C
A
18.1.2 平行四边形的判定
第 3 课时 三角形的中位线
【学习目标】
理解三角形中位线的概念,掌握三角形中位线定理及其应用.
【学习重点】 三角形中位线定理及其应用.
【学习难点】三角形中位线定理的证明.
【 学习过程】
一.课前导学:学生自学课本 47-49 页内容,并完成下列问题:
1. 【探究一】:请同学们思考将任意一个三角形 分成四个全等的三角
形,
你是如何切割的?
2. 【探究二】:三角形中位线概念
连接三角形 的线段叫做三角形的中位线.
思考:(1)三角形的中位线有几条?
(2)三角形的中位线与中线有什么区别?
(3)三角形的中位线与第三边有怎样的关系?
3.【探究三】:三角形中位线定理
如图,点 D、E、分别为△ABC 边 AB、AC 的中点,求证:DE∥BC 且 DE=
BC.
【思考】:如保将证明 DE= BC 转化为证明两条线段相等,你能构造平行四边形完成本
题的证明吗?相信你能行!
证明:
[来源:Zxxk.Com]
4.三角形中位线定理:三角形的中位线 并且 .
5.课本第 49 页练习 T1、3
2
1
2
1
二、合作、交流、展示:
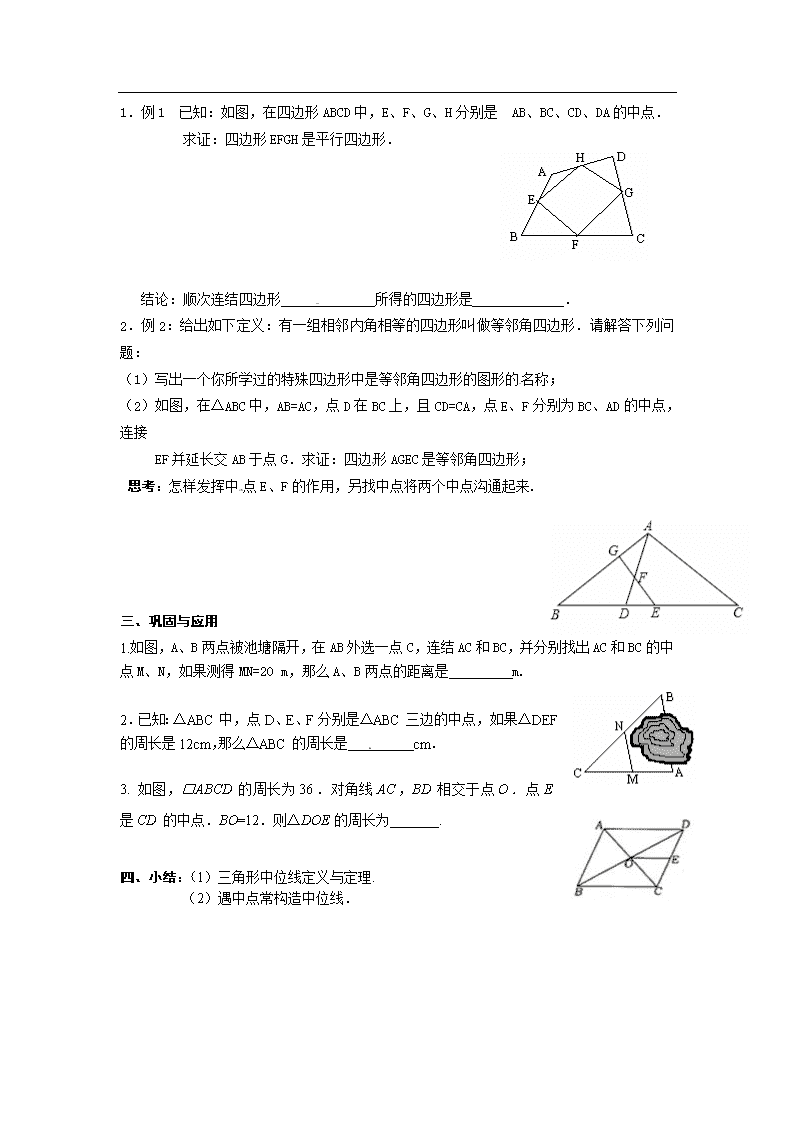
1.例 1 已知:如图,在四边形 ABCD 中,E、F、G、H 分别是 AB、BC、CD、DA 的中点.
求证:四边形 EFGH 是平行四边形.
[来源:Zxxk.Com]
结论:顺次连结四边形 所得的四边形是 .
2.例 2:给出如下定义:有一组相邻内角相等的四边形叫做等邻角四边形.请解答下列问
题:
(1)写出一个你所学过的特殊四边形中是等邻角四边形的图形的 名称;
(2)如图,在△ABC 中,AB=AC,点 D 在 BC 上,且 CD=CA,点 E、F 分别为 BC、AD 的中点,
连接
EF 并延长交 AB 于点 G.求证:四边形 AGEC 是等邻角四边形;
思考:怎样发挥中 点 E、F 的作用,另找中点将两个中点沟通起来.[来源:Z*xx*k.Com][来源:学科网]
[来源:学+科+网]
三、巩固与应用
1.如图,A、B 两点被池塘隔开,在 AB 外选一点 C,连结 AC 和 BC,并分别找出 AC 和 BC 的中
点 M、N,如果测得 MN=20 m,那么 A、B 两点的距离是 m.
2.已知:△ABC 中,点 D、E、F 分别是△ABC 三边的中点,如果△DEF
的周长是 12cm,那么△ABC 的周长是 cm.
3. 如图,□ABCD 的周长为 36 .对角线 AC ,BD 相交于点 O .点 E
是 CD 的中点.BO=12.则△DOE 的周长为 .
四、小结:(1)三角形中位线定义与定理.
(2)遇中点常构造中位线.
相关文档
- 上海教育版数学七下第十四章《三角2021-04-12 22:55:404页
- 2020版高中数学 第一章 解三角形同2021-04-12 22:54:275页
- 2019届二轮复习三角函数、解三角形2021-04-12 22:11:5214页
- 2020版高考数学二轮复习 专题三 三2021-04-12 21:42:425页
- 中考数学专题复习练习:三角形的角平2021-04-12 21:41:394页
- 三年级上册数学教案-5几何小实践(三2021-04-12 21:39:513页
- 中考解直角三角形培优题2021-04-12 21:33:416页
- 八年级下数学课件八年级下册数学课2021-04-12 21:31:5214页
- 中考数学复习训练题29三角形与全等2021-04-12 21:30:423页
- 【数学】2018届一轮复习北师大版第2021-04-12 21:17:2914页