七年级下数学课件《平行线的性质》课件4_冀教版 16页

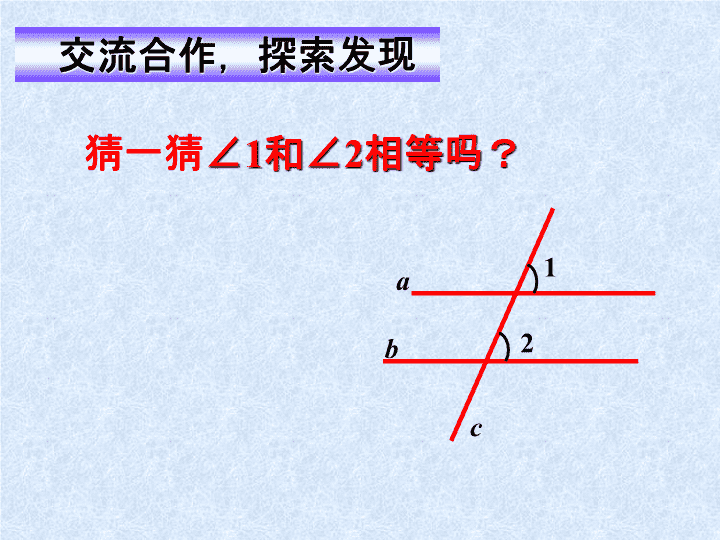
复习回顾 两直线平 行 平行线的判定方法是什么？ 反过来，如果两条直线平行，同位角、 内错角、同旁内角各有什么关系呢? b 1 2 a c 是不是任意一条直线去截平行线a、b 所得的同位角都相等呢？zxxk 两直线平行，同位角相等. 两条平行线被第三条直线所截， 同位角相等. ∵a∥b， 简写为： 符号语言: b 1 2 a c 如图：已知a//b，那么2与3相等吗？为什么? 解∵a∥b(已知), ∴∠1=∠2(两直线平行, 同位角相等). 又∵ ∠1与∠3是对顶角 ∴∠1=∠3(对顶角相等), 由∠1=∠2， ∠1=∠3可得∠2=∠3 b 1 2 a c 两直线平行，内错角相等. 两条平行线被第三条直线所截， 内错角相等.z.x.x.k ∵a∥b，符号语言: 简写为： b 1 2 a c 解：∵a//b （已知）, 如图，已知a//b，那么2与4有什么 关系呢？为什么? ∴ 1=  2（两直线平行， 同位角相等）. ∵  1与 4互补 ∴ 2+  4=180° 由 1=  2，  2+  4=180° 可得  2+  4=180° 两直线平行，同旁内角互补. 两条平行线被第三条直线所截， 同旁内角互补. ∵a∥b,符号语言: 简写为： b 1 2 a c 例1 已知：如图，a∥b，c∥d，∠1=73°.求∠2 和∠3的度数. 解：∵a∥b（已知）. ∴∠1=∠2（两直线平行内 错角相等）. ∵∠1=73°（已知）， ∴∠2=73°（等量代换）. ∵c∥d（已知） ∴∠2+∠3=180°（两直线 平行，同旁内角互补， ∴∠3=180°-∠2（等式的性质）， ∴∠3=180°-73°=107°（等量代换）. 例题解析 例2 已知：如图∠ 1=∠2对∠3= ∠4，说明理由. 理由： ∵ ∠ 1=∠2 （已知）. ∴AB∥CD（内错角相等，两直线 平行）. ∴∠3= ∠4 °（两直线平行，内 错角相等）. 理由：∵ a ∥ b （ ）， 1.为下面的说理过程填空： 已知：如图，直线a，b被直线c所截，a ∥ b， a ⊥c. ∵ ∠1 = 90°（ ）. 对b ⊥c说明理由. 2 c a 1 b ∴∠1= _____ （ ）. ∴∠2= （ ）. ∴ b ⊥c （ ）. 已知 ∠2 两直线平行，同位角相等 a ⊥c 90° 等量代换 垂直的性质 练习 2、已知：如图，点B，A，E在一条直线上， ∠1＝∠B.求证：∠C＝∠2. 证明：∵ ∠1＝∠B， ( ) ∴AD∥BC. ( ) ∴ ∠C＝∠2. ( ) 已知条件 同位角相等，两直线平行 两直线平行，内错角相等 1 2 A B C D E 1.如图在四边形ABCD中，已知AB∥CD， ∠B = 60°. ①求∠C的度数; ②由已知条件能否求得∠A的度数? A B C D 2.如图，在汶川大地震当中，一辆抗震救灾汽车 经过一条公路两次拐弯后，和原来的方向相同， 也就是拐弯前后的两条路互相平行.第一次拐的 角∠B等于142°，第二次拐的角∠C是多少度？ 为什么？ 142° B C A D ？ 性质1：两直线平行，同位角相等． 性质2：两直线平行，内错角相等． 性质3：两直线平行，同旁内角互补． 平行线的性质：