高考数学复习中档解答题规范训练(二) 10页

‎ ‎ 中档解答题规范训练(二)‎ 概率与统计 ‎(建议用时:45分钟)‎ ‎1.(2014·汕头模拟)某校高三数学竞赛初赛后,对考生成绩进行统计(考生成绩均不低于90分,满分150分)将成绩按如下方式分成六组,第一组[90,100),第二组[100,110),……,第六组[140,150].如图所示为其频率分布直方图的一部分,第四组,第五组,第六组的人数依次成等差数列,且第六组有4人.‎ ‎(1)请补充完整频率分布直方图,并估计这组数据的平均数M.(计算时可以用组中值代替各组数据的平均值)‎ ‎(2)现根据初赛成绩从第四组和第六组中任意选2人,记他们的成绩分别为x,y,若|x-y|≥10,则称此2人为“黄金帮扶组”,试求选出的2人为“黄金帮扶组”的概率.‎ ‎【解析】(1)设第四组,第五组的频率分别为m,n,‎ 则2n=m+0.005×10,①‎ m+n=1-(0.005+0.015+0.020+0.035)×10.②‎ 由①②解得m=0.15,n=0.1,‎ M=95×0.2+105×0.15+115×0.35+125×0.15+135×0.1+145×0.05=114.5.(补图略)‎ ‎(2)依题意,知第四组人数为4×=12人,而第六组有4人,‎ 所以第四组和第六组一共有16人,从中任选2人,一共有=120(种)选法,‎ 若满足|x-y|≥10,‎ 则一定是分别从两个小组中各选1人,‎ 因此有=48(种)选法,‎ 所以选出的2人为“黄金帮扶组”的概率P==.‎ ‎【加固训练】(2014·合肥模拟)某校设计了一个物理学科的实验考查:考生从6道备选题中一次性随机抽取3道题,按照要求独立完成实验操作.规定:至少正确完成其中2道题的便可通过考查.已知6道备选题中,考生甲有4道题能正确完成,2道题不能完成;考生乙每题正确完成的概率都是,且各题正确完成与否互不影响.‎ ‎(1)求考生甲通过实验考查的概率.‎ ‎(2)求甲、乙两考生正确完成题数x1,x2的概率分布列.‎ ‎(3)试用统计知识分析比较甲、乙两考生的实验操作能力的稳定性.‎ ‎【解析】(1)考生甲要通过实验考查,就必须正确完成所抽3道题中的2道题或3道题.故所求概率为:‎ P==.‎ ‎(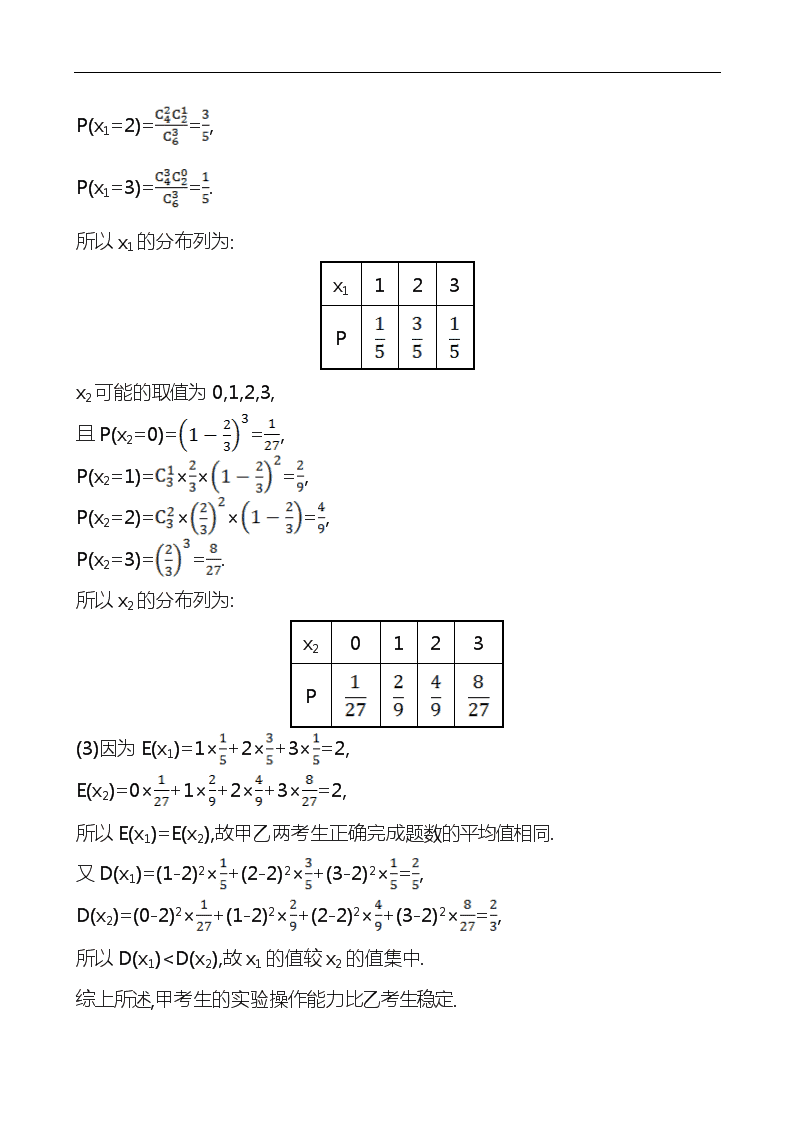2)x1可能的取值为1,2,3,‎ 且P(x1=1)==,‎ P(x1=2)==,‎ P(x1=3)==.‎ 所以x1的分布列为:‎ x1‎ ‎1‎ ‎2‎ ‎3‎ P x2可能的取值为0,1,2,3,‎ 且P(x2=0)==,‎ P(x2=1)=××=,‎ P(x2=2)=××=,‎ P(x2=3)==.‎ 所以x2的分布列为:‎ x2‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎(3)因为E(x1)=1×+2×+3×=2,‎ E(x2)=0×+1×+2×+3×=2,‎ 所以E(x1)=E(x2),故甲乙两考生正确完成题数的平均值相同.‎ 又D(x1)=(1-2)2×+(2-2)2×+(3-2)2×=,‎ D(x2)=(0-2)2×+(1-2)2×+(2-2)2×+(3-2)2×=,‎ 所以D(x1)3.841.‎ 所以,据此统计可在犯错误的概率不超过0.05的前提下认为选做“几何类”或“代数类”与性别有关.‎ ‎(2)由题可知在选做《不等式选讲》的18位同学中,要选取3位同学.‎ ‎①方法一:令事件A为“这名班级学习委员被抽到”;‎ 事件B为“两名数学课代表被抽到”,‎ 则P(A∩B)=,P(A)=.‎ 所以P(B|A)====.‎ 方法二:令事件C为“在这名学委被抽到的条件下,两名数学课代表也被抽到”,‎ 则P(C)===.‎ ‎②由题知X的可能值为0,1,2.‎ 依题意P(X=0)==;‎ P(X=1)==;P(X=2)==.‎ 从而X的分布列为:‎ X ‎0‎ ‎1‎ ‎2‎ P 于是E(X)=0×+1×+2×==.‎ ‎4.(2014·韶关模拟)某网络营销部门为了统计某市网友‎2013年11月11日在某淘宝店的网购情况,随机抽查了该市当天60名网友的网购金额情况,得到如下数据统计表(如图(1)):‎ 网购金额(单位:千元)‎ 频数 频率 ‎[0,0.5]‎ ‎3‎ ‎0.05‎ ‎(0.5,1]‎ x p ‎(1,1.5]‎ ‎9‎ ‎0.15‎ ‎(1.5,2]‎ ‎15‎ ‎0.25‎ ‎(2,2.5]‎ ‎18‎ ‎0.30‎ ‎(2.5,3]‎ y q 合计 ‎60‎ ‎1.00‎ ‎(1)‎ ‎(2)‎ 若网购金额超过2千元的顾客定义为“网购达人”,网购金额不超过2千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为3∶2.‎ ‎(1)试确定x,y,p,q的值,并补全频率分布直方图(如图(2)).‎ ‎(2)该营销部门为了进一步了解这60名网友的购物体验,从“非网购达人”“网购达人”中用分层抽样的方法确定10人,若需从这10人中随机选取3人进行问卷调查.设ξ为选取的3人中“网购达人”的人数,求ξ的分布列和数学期望.‎ ‎【解析】(1)根据题意,有:‎ 解得所以p=0.15,q=0.10.‎ 补全频率分布直方图如图所示.‎ ‎(2)用分层抽样的方法,从中选取10人,则其中“网购达人”有10×=4(人),‎ ‎“非网购达人”有10×=6(人).‎ 故ξ的可能取值为0,1,2,3;‎ P(ξ=0)==,P(ξ=1)==,‎ P(ξ=2)==,P(ξ=3)==,‎ 所以ξ的分布列为:‎ ξ ‎0‎ ‎1‎ ‎2‎ ‎3‎ P 所以E(ξ)=0×+1×+2×+3×=.‎ ‎【加固训练】已知一个口袋分别装了3个白色玻璃球、2个红色玻璃球和n个黑色玻璃球,现从中任取2个玻璃球进行观察,每取到一个白色玻璃球得1分,每取到一个红色玻璃球得2分,每取到一个黑色玻璃球得0分,用X表示所得的分数,已知得0分的频率为.‎ ‎(1)求袋中黑色玻璃球的个数n.‎ ‎(2)求X的分布列.‎ ‎(3)求得分不低于3分的概率.‎ ‎【解析】(1)因为P(X=0)==,‎ 所以n2-3n-4=0,‎ 解得n=-1(舍去)或n=4,‎ 即袋中有4个黑色玻璃球.‎ ‎(2)由题意知,X的可能取值为0,1,2,3,4.‎ 则P(X=0)=,‎ P(X=1)==,‎ P(X=2)==,‎ P(X=3)==,‎ P(X=4)==,‎ 所以X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ P ‎(3)得分不低于3分,即X≥3,‎ 由(2)知X=3或X=4,‎ 因此P(X≥3)=P(X=3)+P(X=4)=+=,即得分不低于3分的概率为.‎ 关闭Word文档返回原板块