2014年高考试题——数学理（江西卷）解析版 13页

2014 年江西卷高考理科数学试题逐题详解 (解析版) 一．选择题：本大题共 10 小题，每小题 5 分，共 50 分. 在每小题给出的四个选项中，只 有一项是符合题目要求的。 【2014 年江西卷（理 01）】 z 是 z 的共轭复数. 若 2 zz ，（ 2)(  izz （i 为虚数单 位），则 z A. i1 B. i1 C. i1 D. i1 【答案】D 【解析】   2, ( , ) 1 22 1 1 Z Z Z a bi a b R a Z Z i Z b b Zi                Q Q 【2014 年江西卷（理 02）】 函数 )ln()( 2 xxxf  的定义域为 A. )1,0( B. ]1,0[ C. ),1()0,(   D. ),1[]0,(   【答案】C 【解析】 2 0 10 xx xx     Q 或 【2014 年江西卷（理 03）】已知函数 ||5)( xxf  ， )()( 2 Raxaxxg  ，若 1)]1([ gf ， 则 a A. 1 B. 2 C. 3 D. 1 【答案】A 【解析】      015 10 10 1 f g x g a a       Q 【2014 年江西卷（理 04）】在 ABC 中，内角 A,B,C 所对的边分别是 ,,, cba ，若 ,3,6)( 22  Cbac 则 的面积是 A.3 B. 2 39 C. 2 33 D. 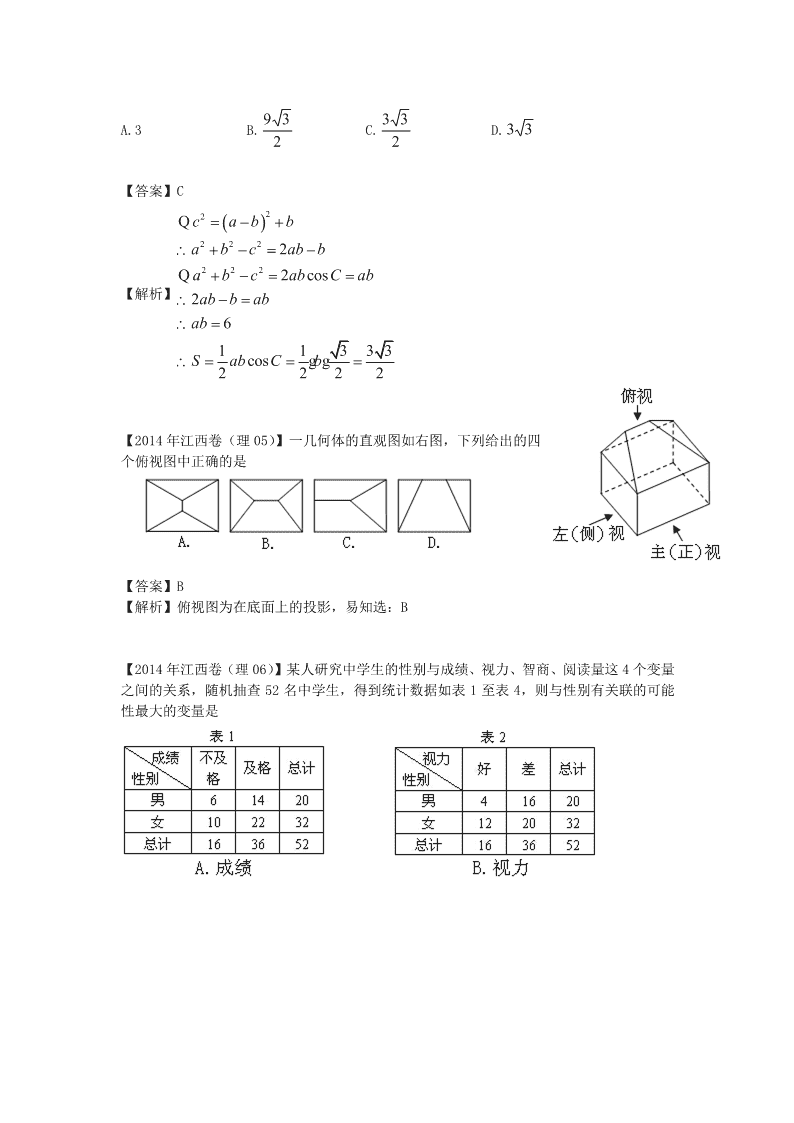33 【答案】C 【解析】  22 2 2 2 2 2 2 2 2 cos 2 6 1 1 3 3 3cos2 2 2 2 c a b b a b c ab b a b c ab C ab ab b ab ab S ab C b                     Q Q gg 【2014 年江西卷（理 05）】一几何体的直观图如右图，下列给出的四 个俯视图中正确的是 【答案】B 【解析】俯视图为在底面上的投影，易知选：B 【2014 年江西卷（理 06）】某人研究中学生的性别与成绩、视力、智商、阅读量这 4 个变量 之间的关系，随机抽查 52 名中学生，得到统计数据如表 1 至表 4，则与性别有关联的可能 性最大的变量是 【答案】D 【解析】根据独立性检验相关分析知，阅读量与性别相关数据较大，选 D 【2014 年江西卷（理 07）】阅读如下程序框图，运行相应的程序，则程序运行后输出的结果 为 A.7 B.9 C.10 D.11 【答案】B 【解析】 1 3 5 7 9 10 lg lg lg lg lg lg 13 5 7 9 11 11S          ， 9i ，选 B 【2014 年江西卷（理 08）】若 12 0 ( ) 2 ( ) ,f x x f x dx 则 1 0 ()f x dx  A. 1 B. 1 3 C. 1 3 D.1 【答案】B 【解析】设  1 0 m f x dx  ， 则 2( ) 2f x x m ，   1 1 1 123 0 0 0 0 11( ) 2 ( ) 2 233f x dx x f x dx dx x mx m m         ， 所以 1 3m  . 【2014 年江西卷（理 09）】在平面直角坐标系中， ,AB分别是 x 轴和 y 轴上的动点，若以 AB 为直径的圆C 与直线 2 4 0xy   相切，则圆C 面积的最小值为 A. 4 5 B. 3 4  C.(6 2 5) D. 5 4  【答案】A 【解析】原点 O 到直线 2 4 0xy   的距离为d ，则 5 4d ，点 C 到直线 的距离是圆的半径 r ，由题意知 C 是 AB 的中点，又以斜边为直径的圆过三个顶点，则在直 角 AOB 中三角形中，圆 C 过原点 O，即||OC r ，圆 C 的轨迹为抛物线，O 为焦点，l 为 准线，所以 5 2 2min  dr ， 5 42 min   rS ，所以选 A。 【2014 年江西卷（理 10）】 如右图，在长方体 1 1 1 1ABCD A B C D 中， AB =11， AD =7， 1AA =12，一质点从顶点 A 射向点  4 312E ，， ，遇长方体的面反射（反射服从光的反射原理）， 将 1i  次到第 i 次反射点之间的线段记为  2,3,4iLi ， 1L AE ，将线段 1 2 3 4, , ,L L L L 竖直放置在同一水平线上，则大致的图形是 【答案】C 【解析】 A(0,0,0),E(4,3,12), 1E (8,6,0), 2E ( 3 28 ,7,4), 3E (11, 4 25 ,9), 131234 222 AE ， 534 22 1 EE , 3 13413 4 22 2 21   EE , 21 2 22 32 12 6554 5 3 5 EEEE      二.选做题：请考生在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分， 本题共 5 分.在每小题给出的四个选项中，只有一项是符合题目要求的. 【2014 年江西卷（理 11）】 (1).（不等式选做题）对任意 ,x y R , 1 1 1x x y y      的最小值为 A.1 B. 2 C.3 D. 4 【答案】B 【解析】  | 1| | | | 1| | 1 | 1 | | 1 1 | 1 2 3x x y y x x y y                【2014 年江西卷（理 11）】 (2).（坐标系与参数方程选做题）若以直角坐标系的原点为极点， x 轴的非负半轴为极轴建立极坐标系，则线段  1 0 1y x x    的极坐标为（ ） A. 1 ,0cos sin 2    B. 1 ,0cos sin 4    C. cos sin ,0 2        D. cos sin ,0 4        【答案】A 【解析】Q 1yx  01x  sin 1 cos     0 cos 1 1 0sin cos 2       所以选 A。 三.填空题：本大题共 4 小题，每小题 5 分，共 20 分. 【2014 年江西卷（理 12）】 10 件产品中有 7 件正品，3 件次品，从中任取 4 件，则恰好取到 1 件次品的概率是________. 【答案】 1 2 【解析】 13 37 4 10 1 2 CCP CQ 【2014 年江西卷（理 13）】若曲线 xye 上点 P 处的切线平行于直线 2 1 0xy   ，则点 的坐标是________. 【答案】 ln 2,2 【解析】   0 0 0 ' 00 0 , 2 2 2 ( ln 2,2) x x x x x ye ye P x y e e ye P                Q Q 设 【2014 年江西卷（理 14）】已知单位向量 1e 与 2e 的夹角为 ，且 1cos 3  ，向量 1232a e e与 123b e e的夹角为  ，则cos = 【答案】 22 3 【解析】 2 cos 19 4 2 3 2 93 19 1 2 3 1 83 19 2 9 1 1 83 8 2 2cos 33 2 2 ab ab a b ab                             rr Q rr r r rr 【 2014 年 江 西 卷 （ 理 15 ）】 过 点 (1,1)M 作斜率为 1 2 的直线与椭圆C ： 22 221( 0)xy abab    相交于 ,AB，若 M 是线段 AB 的中点，则椭圆 的离心率为 【答案】 2 2 【解析】           1 1 2 2 22 11 22 22 22 22 1 2 1 2 1 2 1 2 22 22 22 ,, 1 1 0 1 22 2 0 2 2 2 A x y B x y xy ab xy ab x x x x y y y y ab ab ab e               设 则 四.简答题：本大题共 6 小题，共 75 分.解答应写出文字说明，证明过程或演算步骤. 【2014 年江西卷（理 16）】（本小题满分 12 分） 已知函数 ( ) sin( ) cos( 2 )f x x a x    ，其中 , ( , )22aR    （1）当 2, 4a 时，求 ()fx在区间[0, ] 上的最大值与最小值； (2)若 ( ) 0, ( ) 12ff ，求 ,a  的值. 【解析】（1） 2, 4a , ( ) sin( ) cos( 2 ) sin( ) 2 cos( )42f x x a x x x         22sin cos 2 sin22 22cos sin22 cos 4 x x x xx x       ……………………………………………………………3 分 0 x 又 ， 5 4 4 4x      …………………………………………………………4 分   21 2fx      min max 21, 2f x f x    ；……………………………………………………………6 分 (2) ( ) sin( ) cos( 2 ) cos sin 2 cos 2sin cos 02 2 2f a a a                 又 ( , )22   ， cos 0, 2 sin 1a    …………………………………………7 分 ( ) sin( ) cos( 2 ) sin cos2 1f a a               2sin 1 2sin 1a    2sin 2 sin 1aa    ，…………………………………………8 分 1a   …………………………………………10 分 1sin 2   ，又 ( , )22   ，所以 6   ………………12 分 【2014 年江西卷（理 17）】（本小题满分 12 分） 已 知 首 项 都 是 1 的两个数列 （ ） ， 满 足 . (1) 令 ，求数列 的通项公式； (2) 若 ，求数列 的前 n 项和 . 【解析】（1） 1 1 12 0, 0n n n n n n na b a b b b b      同时除以 1nnbb ，得到 1 1 20nn nn aa bb      ……………………………………………………2 分 1 1 2nn nn aa bb      即： 1 2nncc ……………………………………………………3 分 所以， nc 是首项为 1 1 1a b  ，公差为 2 的等差数列…………………………………4 分 所以， 1 2( 1) 2 1nc n n     ……………………………………………………5 分 (2) 21n n n acnb   ，   12 1 3n nan    ………………………………………6 分    2 3 4 11 3 3 3 5 3 2 3 3 2 1 3nn nS n n                  3 4 5 1 23 1 3 3 3 5 3 2 3 3 2 1 3nn nS n n              ………………………9 分 两式相减得：      2 3 4 1 2 22 3 2 3 3 3 2 1 3 18 2 2 3n n n nS n n                 …………………11 分   29 1 3n nSn     …………………12 分 【2014 年江西卷（理 18）】（本小题满分 12 分） 已知函数 . (1) 当 时，求 的极值； (2) 若 在区间 上单调递增，求 b 的取值范围. 【解析】1）当 b=2 时，    = x+2 - xfx 2 12 的定义域为 1- 2  ，          2' 52112 2 1 2 2 22 1 2 1 2 xxf x x x x xx         令  ' 0fx ，解得 12x 2, 0x   当 1x 2 x< 2 和0< 时，  ' 0fx ，所以 ()fx在  1, 2 , 2    ,0 上单调递减； 当 12 x< 2 < 时，  ' 0fx ，所以 在 12, 2  上单调递增； 所以，当 x2 时， 取得极小值 ( 2) 0f ；当 1x 2 时， 取得极大值 (0) 4f  。 （2）  fx在 10, 3   上单调递增   ' 0,fx 且不恒等于 0 对 x 10, 3  恒成 立……………………7 分         2 '21 1 5 2 32 1 2 22 1 2 1 2 x x bxf x x b x x bx b xx            25 3 2 0x bx x    ……………………………………8 分 min 25 3 xb  ……………………………………10 分 1252 5 13 3 3 9 x  ……………………………………11 分 1 9b ……………………………………12 分 【2014年江西卷（理19）】 (本小题满分12分) 如图，四棱锥 ABCDP 中， ABCD 为矩形，平面 PAD 平面 . （1）求证： ;PDAB  （2）若 ,2,2,90  PCPBBPC  问 AB 为何值时，四棱锥 ABCDP 的体积最 大？并求此时平面 PBC 与平面 DPC 夹角的余弦值. 【解析】 解：（1）Q 面 PAD 面 ABCD,面 PAD  面 = AD , AB AD AB面 ABCD……………………………………2 分 又 PD Q 面 ABCD……………………………………3 分 AB PD ……………………………………4 分 (2)过 P 作 PO AD ,由（1）有 PO  面 ABCD, 作OM BC ,连接 PM，作 PM BC ……………………………………5 分 设 AB=x. 2 2 41 1 1 4 16 8 63 3 3 3 3P ABCD ABCDV OP S OP AB BC x x x x           gg …7 分 当 2 2 3x  即 6 3x  时， max 26 9V  ……………………………………9 分 如图建立空间直角坐标系， 60,0, 3P  , 60, ,03M   , 66, ,033C  6 ,0,03D ,  660, ,33PM  uuur , 6 6 6,,3 3 3PC    uuur , 6 ,0,03MC  uuur 66,0,33PD    uuur , 60, ,03DC   uuur ……………………………………10 分 设面 PMC 、面 PDC 的法向量分别为  1 1 1,,m x y z ur ，  2 2 2,,n x y z r  0 0 0 m PM m PC m MC      ur uuur g ur uuur g ur uuur g 11 1 1 1 1 66033 6 6 6 03 3 3 6 03 yz x y z x            设 1 1y  ，则 1 1z  ，  0,1,1m  ur 同理可得  1,1,1m  ur ……………………………………11 分 6cos , 3 mnmn mn  ur rur r gur r 平面 PBC 与平面 DPC 夹角的余弦值为 6 3 。…………………………………12 分 【2014 年江西卷（理 20）】（本小题满分 13 分） 如图，已知双曲线 )0(1: 2 2 2  aya xC 的右焦点 F,点 A,B 分别在C 的两条渐近线上， AF⊥x 轴，AB⊥OB,BF∥OA(O 为坐标原点)， （1）求双曲线 的方程； （2）过C 上一点 P(x0,y0)(y0 0 )的直线l ： 102 0  yy a xx 与直线 AF 相交于点 M，与直线 2 3x 相交于点 N。证明：当点 P 在 上移动时， || || NF MF 恒为定值，并求此定值。 【答案】（1） 13 2 2  yx （2） 3 32 【解析】(1)A( a cc, ),B( a tt , ) 11    atc a tc 且 tc a t a 1 ，即 2 ct  ， 3a …………………………… 4 分 即 …………………………………………………………………… 6分 （2）A(2， 3 32 )， 13: 0 0  yyxxl ，F（2,0）， M(2， 0 0 3 32 y x  )，N( 2 3 ， 0 0 2 2 y x  )………………………………………………… 9 分   3 32 3 |32| |32| 3 2 )2(133 |32|2 )2(3 |32|2 4 2 4 1 3 |32| 0 0 2 0 2 0 0 2 0 2 0 0 2 0 2 0 0 0          x x xx x xy x y x y x NF MF ……………………………………………………………………… 13 分 【2014 年江西卷（理 21）】（本小题满分 13 分）随机将  1,2, ,2 , 2n n N n   这 2n 个连 续正整数分成 A,B 两组，每组 n 个数，A 组最小数为 1a ，最大数为 2a ；B 组最小数为 1b ，最 大数为 2b ，记 2 1 1 2,a a b b    （1）当 3n  时，求 的分布列和数学期望； （2）令 C 表示事件 与 的取值恰好相等，求事件 C 发生的概率 )(CP ； （3）对(2)中的事件 C, C 表示 C 的对立事件，判断 和 )(CP 的大小关系，并说明理 由。 【解析】（1）随机变量 的取值所有可能是：2，3，4，5   3 6 415 5P C    ；   3 6 412 5P C      3 6 633 10P C      3 6 634 10P C     的分布列为：  2 3 4 5 P 1 5 3 10 3 10 1 5 所以， 的数学期望为 1 3 3 1 72 3 4 55 10 10 5 2E          2）事件 与 的取值恰好相等的基本事件： 共     1 2 3 2 2 4 6 2( 2) 2 1123 n n n n C C C CP c nC          2n  时，   2 4 222 3Pc C   3）因为   1P c P c  ，所以要比较  Pc与 Pc  的大小，实际上要比较 与 1 2 的 大小， 由 可知， 当 2n  时，  P c P c   当 3n  时，  P c P c  