上海春季高考数学试题含答案 4页

‎2017年上海春考数学试题 一、填空题：（第1—6题每题4分，第7—12题每题5分，共54分）‎ ‎1．设集合，集合，则 ‎ ‎2．不等式的解集为 ‎ ‎3．若复数满足（为虚数单位），则 ‎ ‎4．若，则 ‎ ‎5．若关于、的方程组无解，则实数 ‎ ‎6．若等差数列的前5项和为，则 ‎ ‎7．若、为圆上的动点，则的最大值为 ‎ ‎8．已知数列的通项公式为，则 ‎ ‎9．若的二项展开式的各项系数之和为，则该展开式中常数项的值为 ‎ ‎10．设椭圆的左、右焦点分别为、，点在该椭圆上，则使得是 ‎ 等腰三角形的点的个数是 ‎ ‎11．设、、…、为1、2、3、4、5、6的一个排列，则满足 ‎ 的不同排列的个数为 ‎ ‎12．设、，若函数在区间上有两个不同的零点，则的取值范围为 ‎ 二、选择题（共4题，每题5分，共20分）‎ ‎13．函数的单调递增区间是（ ）‎ ‎ A B C D ‎ ‎14．设，“”是“”的（ ）条件 A 充分非必要 B 必要非充分 C 充要 D 既非充分也非必要 ‎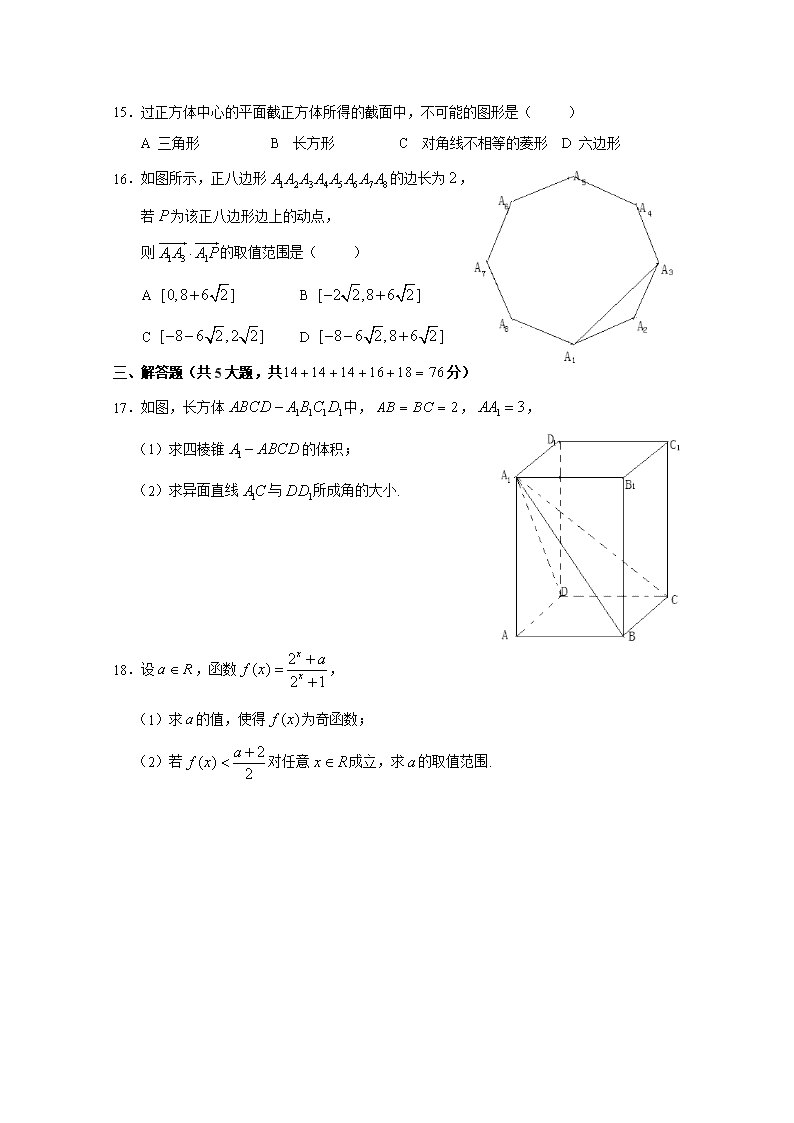15．过正方体中心的平面截正方体所得的截面中，不可能的图形是（ ）‎ ‎ A 三角形 B 长方形 C 对角线不相等的菱形 D 六边形 ‎16．如图所示，正八边形的边长为，‎ 若为该正八边形边上的动点，‎ ‎ 则的取值范围是（ ）‎ A B ‎ C D ‎ 三、解答题（共5大题，共分）‎ ‎17．如图，长方体中，，，‎ ‎ （1）求四棱锥的体积；‎ ‎ （2）求异面直线与所成角的大小.‎ ‎18．设，函数，‎ ‎ （1）求的值，使得为奇函数；‎ ‎（2）若对任意成立，求的取值范围.‎ ‎19．某景区欲建造两条圆形观景步道、（宽度忽略不计），如图所示，已知，‎ ‎ ，（单位：米），要求圆与、分别相切于点、，‎ 圆与、分别相切于点、，‎ ‎（1）若，求圆、的半径（结果精确到米）；‎ ‎ （2）若观景步道与的造价分别为每米千元与每米千元，如何设计圆、的大小，使总造价最低？最低总造价是多少？（结果精确到千元）‎ ‎20．已知双曲线（），直线（），与交于、‎ 两点，为关于轴的对称点，直线与轴交于点，‎ ‎（1）若点是的一个焦点，求的渐近线方程；‎ ‎（2）若，点的坐标为，且，求的值；‎ ‎（3）若，求关于的表达式.‎ ‎21．已知函数，‎ ‎ （1）解方程；‎ ‎（2）设，，证明：，且；‎ ‎（3）设数列中，，，，求的取值范围，‎ 使得对任意成立.‎ ‎【简答】‎ 一、填空题：‎ ‎1. 2. 3. 4. 5. 6. ‎ ‎7. 8. 9. 10. 11. 12. ‎ 二、选择题：‎ ‎13. 14. 15. 16. ‎ 三、解答题：‎ ‎17. （1）4；（2）；‎ ‎18. （1）；（2）‎ ‎19. （1）的半径为，的半径为；‎ ‎（2）的半径为30，的半径为20，总造价为 ‎20. （1）；（2）；‎ ‎21. （1）；（2）作差法