高考卷 06普通高等学校招生全国统一考试（福建卷 13页

2006 年普通高等学校招生全国统一考试（福建卷） （理工农医类） 一．选择题：本大题共 12 小题，每小题 5 分，共 60 分。在每小题给出的四个选项中，只有 一项是符合题目要求的。 （1）设 , , ,a b c R 则复数 ( )( )a bi c di  为实数的充要条件是 （A） 0ad bc  （B） 0ac bd  （C） 0ac bd  （D） 0ad bc  （2）在等差数列 na 中，已知 1 2 32, 13,a a a   则 4 5 6a a a  等于 （A）40 （B）42 （C）43 （D）45 （3）已知 3( , ),sin ,2 5     则 tan( )4   等于 （A） 1 7 （B） 7 （C） 1 7  （D） 7 （4）已知全集 ,U R 且    2| 1 2 , | 6 8 0 ,A x x B x x x       则 ( )U A Bð 等于 （A）[ 1,4) （B） (2,3) （C） (2,3] （D） ( 1,4) （5）已知正方体外接球的体积是 32 3  ，那么正方体的棱长等于 （A） 2 2 （B） 2 3 3 （C） 4 2 3 （D） 4 3 3 （6）在一个口袋中装有 5 个白球和 3 个黑球，这些球除颜色外完全相同。从中摸出 3 个球， 至少摸到 2 个黑球的概率等于 （A） 2 7 （B） 3 8 （C） 3 7 （D） 9 28 （7）对于平面 和共面的直线 m 、 ,n 下列命题中真命题是 （A）若 , ,m m n  则 n ∥ （B）若 m  ∥ ,n∥ ,则 m∥n （C）若 ,m n  ∥ ,则 m∥n （D）若 m 、 n 与 所成的角相等，则 m∥n （8）函数 2log ( 1)1 xy xx   的反函数是 （A） 2 ( 0)2 1 x xy x  （B） 2 ( 0)2 1 x xy x  （C） 2 1( 0)2 x xy x  （D） 2 1( 0)2 x xy x  （9）已知函数 ( ) 2sin ( 0)f x x   在区间 ,3 4      上的最小值是 2 ，则 的最小值 等于 （A） 2 3 （B） 3 2 （C）2 （D）3 （10）已知双曲线 2 2 2 2 1( 0, 0)x y a ba b     的右焦点为 F，若过点 F 且倾斜角为 60o 的直线 与双曲线的右支有且只有一个交点，则此双曲线离心率的取值范围是 （A） (1,2] （B） (1,2) （C）[2, ) （D） (2, ) （11）已知 1, 3, . 0,OA OB OAOB      点 C 在 AOC 30o 。 设 ( , )OC mOA nOB m n R     ，则 m n 等于 （A） 1 3 （B）3 （C） 3 3 （D） 3 （12）对于直角坐标平面内的任意两点 1 1 2 2( , ), ( , )A x y B x y ，定义它们之间的一种“距离”： 2 1 2 1| | .AB x x y y    给出下列三个命题： ①若点 C 在线段 AB 上，则 ;AC CB AB  ②在 ABC 中，若 90 ,oC  则 2 2 2 ;AC CB AB  ③在 ABC 中， .AC CB AB  其中真命题的个数为 （A）0 （B）1 （C）2 （D）3 二．填空题：本大题共 4 小题，每小题 4 分，共 16 分。把答案填在答题卡的相应位置。 （13） 2 51( )x x  展开式中 4x 的系数是 （用数字作答）。 （14）已知直线 1 0x y   与抛物线 2y ax 相切，则 ______.a  （15）一个均匀小正方体的 6 个面中，三个面上标以数 0，两个面上标以 数 1，一个面上标以数 2。将这个小正方体抛掷 2 次，则向上的数之积的 数学期望是 。 （16）如图，连结 ABC 的各边中点得到一个新的 1 1 1,A B C 又连结 1 1 1A B C 的各边中点得到 2 2 2A B C ，如此无限继续下去，得到一系列三角 形： ABC ， 1 1 1A B C ， 2 2 2A B C ，...，这一系列三角形趋向于一个点 M。已知 (0,0), (3,0),A B (2,2),C 则点 M 的坐标是 。 三．解答题：本大题共 6 小题，共 74 分。解答应写出文字说明，证明过程或演算步骤。 （17）（本小题满分 12 分） 已知函数 2 2( ) sin 3sin cos 2cos , .f x x x x x x R    （I）求函数 ( )f x 的最小正周期和单调增区间； （II）函数 ( )f x 的图象可以由函数 sin 2 ( )y x x R  的图象经过怎样的变换得到？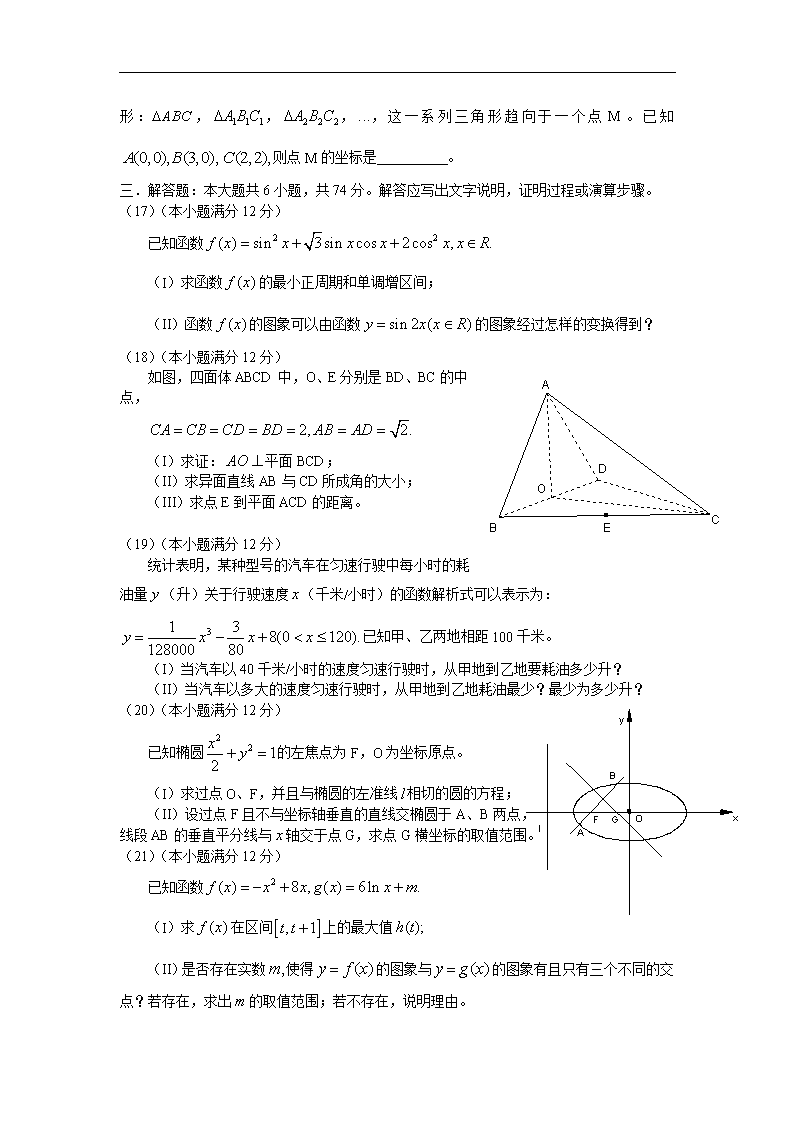 （18）（本小题满分 12 分） 如图，四面体 ABCD 中，O、E 分别是 BD、BC 的中 点， 2, 2.CA CB CD BD AB AD      （I）求证： AO  平面 BCD； （II）求异面直线 AB 与 CD 所成角的大小； （III）求点 E 到平面 ACD 的距离。 （19）（本小题满分 12 分） 统计表明，某种型号的汽车在匀速行驶中每小时的耗 油量 y （升）关于行驶速度 x （千米/小时）的函数解析式可以表示为： 31 3 8(0 120).128000 80y x x x     已知甲、乙两地相距 100 千米。 （I）当汽车以 40 千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？ （II）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？ （20）（本小题满分 12 分） 已知椭圆 2 2 12 x y  的左焦点为 F，O 为坐标原点。 （I）求过点 O、F，并且与椭圆的左准线 l 相切的圆的方程； （II）设过点 F 且不与坐标轴垂直的直线交椭圆于 A、B 两点， 线段 AB 的垂直平分线与 x 轴交于点 G，求点 G 横坐标的取值范围。 （21）（本小题满分 12 分） 已知函数 2( ) 8 , ( ) 6ln .f x x x g x x m     （I）求 ( )f x 在区间 , 1t t  上的最大值 ( );h t （II）是否存在实数 ,m 使得 ( )y f x 的图象与 ( )y g x 的图象有且只有三个不同的交 点？若存在，求出 m 的取值范围；若不存在，说明理由。 （22）（本小题满分 14 分） 已知数列 na 满足 * 1 11, 2 1( ).n na a a n N    （I）求数列 na 的通项公式； C A D B O E （II）若数列{bn}滿足 1 2 11 1 *4 4 4 ( 1) ( ),n nb bb b na n N     证明：数列{bn}是等差数列； （Ⅲ）证明： *1 2 2 3 1 1 ... ( ).2 3 2 n n aa an n n Na a a         2006 年高考(福建卷)数学理试题答案 一．选择题：本大题考查基本概念和基本运算。每小题 5 分，满分 60 分。 （1）D （2）B （3）A （4）C （5）D （6）A （7）C （8）A （9）B （10）C （11）B （12）B 1． , , ,a b c R 复数 ( )( )a bi c di  = ( ) ( )ac bd ad bc i   为实数，∴ 0ad bc  ，选 D. 2．在等差数列 na 中，已知 1 2 32, 13,a a a   ∴ d=3，a5=14， 4 5 6a a a  =3a5=42，选 B. 3．已知 3( , ),sin ,2 5     则 3tan 4    ， tan( )4   =1 tan 1 1 tan 7     ，选 A. 4 ． 全 集 ,U R 且  | 1 2 { | 1或 3},A x x x x x        2| 6 8 0 { | 2 4},B x x x x x       ∴ ( )U A Bð = (2,3] ，选 C. 5．正方体外接球的体积是 32 3  ，则外接球的半径 R=2，正方体的对角线的长为 4，棱长等 于 4 3 3 ，选 D. 6．在一个口袋中装有 5 个白球和 3 个黑球，这些球除颜色外完全相同。从中摸出 3 个球， 至少摸到 2 个黑球的概率等于 2 1 3 3 5 3 3 8 C C CP C  = 2 7 ，选 A。 7．对于平面 和共面的直线 m 、 ,n 真命题是“若 ,m n  ∥ ,则 m∥n ”，选 C. 8 ． 对 于 x>1 ， 函 数 2 2 1log log (1 )1 1 xy x x     >0 ， 解 得 1 2 11 y x   ， 1 12 1yx   = 2 2 1 y y  ，∴ 原函数的反函数是 2 ( 0)2 1 x xy x  ，选 A. 9．函数 ( ) 2sin ( 0)f x x   在区间 ,3 4      上的最小值是 2 ，则ωx 的取值范围是 ,3 4      ， ∴ 3 2   ≤ 或 3 4 2  ≥ ，∴  的最小值等于 3 2 ，选 B. 10．已知双曲线 2 2 2 2 1( 0, 0)x y a ba b     的右焦点为 F，若过点 F 且倾斜角为 60o 的直线与 双曲线的右支有且只有一个交点，则该直线的斜率的绝对值小于等于渐近线的斜率 b a ，∴ b a ≥ 3 ，离心率 e2= 2 2 2 2 2 c a b a a  ≥4 ，∴ e≥2，选 C 11．已知 1, 3, . 0,OA OB OAOB      点 C 在 AB 上，且 AOC 30o 。 设 A 点坐标 为 (1 ， 0) ， B 点 的 坐 标 为 (0 ， 3 ) ， C 点 的 坐 标 为 (x ， y)=( 3 4 ， 3 4 ) ， ( , )OC mOA nOB m n R     ，则∴ m= 4 3 ，n= 4 1 ， m n =3，选 B. 12．对于直角坐标平面内的任意两点 1 1 2 2( , ), ( , )A x y B x y ，定义它们之间的一种“距离”： 2 1 2 1| | .AB x x y y    ①若点 C 在线段 AB 上，设 C 点坐标为(x0，y0)，x0 在 x1 、 x2 之 间 ， y0 在 y1 、 y2 之 间 ， 则 0 1 0 1 2 0 2 0| | | | | | | |AC CB x x y y x x y y         = 2 1 2 1 | | .x x y y AB    ③在 ABC 中， 0 1 0 1 2 0 2 0| | | | | | | |AC CB x x y y x x y y         > 0 1 2 0 0 1 2 0| ( ) ( ) | | ( ) ( ) |x x x x y y y y       = 2 1 2 1 | | .x x y y AB    ∴命题① ③成立，而命题②在 ABC 中，若 90 ,oC  则 2 2 2 ;AC CB AB  明显不成立，选 B. 二．填空题：本大题考查基础知识和基本运算。每小题 4 分满分 16 分。 （13）10 （14） 1 4 （15） 4 9 （16） 5 2( , )3 3 13． 2 51( )x x  展开式中， 4x 项为 2 2 3 2 4 3 1 5 1( ) ( ) 10T C x xx     ，该项的系数是 10. 14 ． 已 知 直 线 1 0x y   与 抛 物 线 2y ax 相 切 ， 将 y=x － 1 代 入 抛 物 线 方 程 得 2 1 0ax x   ，∴ 1 4 0a   ，a= 4 1 。 15．一个均匀小正方体的 6 个面中，三个面上标以数 0，两个面上标以数 1，一个面上标以 数 2 。 将 这 个 小 正 方 体 抛 掷 2 次 ， 向 上 的 数 之 积 可 能 为 ξ=0 ， 1 ， 2 ， 4 ， 则 1 1 1 1 1 1 3 3 3 3 3 3 1 1 6 6 3( 0) 4 C C C C C CP C C      ， 1 1 2 2 1 1 6 6 1( 1) 9 C CP C C     ， 1 1 1 1 2 1 1 2 1 1 6 6 1( 2) 9 C C C CP C C     ， 1 1 1 1 1 1 6 6 1( 4) 36 C CP C C     ， ∴ 1 2 4 4 9 9 36 9E     . 16．如图，连结 ABC 的各边中点得到一个新的 1 1 1,A B C 又连结 1 1 1A B C 的各边中点得到 2 2 2A B C ，如此无限继续下去，得到一系列三角形： ABC ， 1 1 1A B C ， 2 2 2A B C ，...， 这一系列三角形趋向于一个点 M。已知 (0,0), (3,0),A B (2,2),C 则点 M 的坐标是 ABC 的 重心，∴ M= 5 2( , )3 3 三．解答题：本大题共 6 小题，共 74 分。解答应写出文字说明，证明过程或演算步骤。 （17）本小题主要考查三角函数的基本公式、三角恒等变换、三角函数的图象和性质等基本 知识，以及推理和运算能力。满分 12 分。 解：（I） 1 cos2 3( ) sin 2 (1 cos2 )2 2 xf x x x    3 1 3sin 2 cos22 2 2 3sin(2 ) .6 2 x x x        ( )f x 的最小正周期 2 .2T    由题意得 2 2 2 , ,2 6 2k x k k Z         即 , .3 6k x k k Z       ( )f x 的单调增区间为 , , .3 6k k k Z        （II）方法一： 先把 sin 2y x 图象上所有点向左平移 12  个单位长度，得到 sin(2 )6y x   的图象， 再把所得图象上所有的点向上平移 3 2 个单位长度，就得到 3sin(2 )6 2y x    的图象。 方法二： 把 sin 2y x 图象上所有的点按向量 3( , )12 2a   平移，就得到 3sin(2 )6 2y x    的图象。 （18）本小题主要考查直线与平面的位置关系、异面直线所成的角以及点到平面的距离基本 知识，考查空间想象能力、逻辑思维能力和运算能力。满分 12 分。 方法一： （I）证明：连结 OC , , .BO DO AB AD AO BD    , , .BO DO BC CD CO BD    在 AOC 中，由已知可得 1, 3.AO CO  而 2,AC  2 2 2 ,AO CO AC   90 ,oAOC  即 .AO OC ,BD OC O  AO  平面 BCD （II）解：取 AC 的中点 M，连结 OM、ME、OE，由 E 为 BC 的中点知 ME∥AB,OE∥DC 直线 OE 与 EM 所成的锐角就是异面直线 AB 与 CD 所成的角 在 OME 中， 1 2 1, 1,2 2 2EM AB OE DC    OM 是 直 角 AOC 斜 边 AC 上 的 中 线 ， 1 1,2OM AC   2cos ,4OEM   异面直线 AB 与 CD 所成角的大小为 2arccos .4 （III）解：设点 E 到平面 ACD 的距离为 .h , 1 1. . . .3 3 E ACD A CDE ACD CDE V V h S AO S         在 ACD 中， 2, 2,CA CD AD   2 21 2 72 2 ( ) .2 2 2ACDS      而 21 3 31, 2 ,2 4 2CDEAO S     31. 212 .77 2 CDE ACD AO Sh S        点 E 到平面 ACD 的距离为 21 .7 方法二： （I）同方法一。 （II）解：以 O 为原点，如图建立空间直角坐标系，则 (1,0,0), ( 1,0,0),B D  A B M D E O C 1 3(0, 3,0), (0,0,1), ( , ,0), ( 1,0,1), ( 1, 3,0).2 2C A E BA CD      . 2cos , ,4 BACDBA CD BA CD          异面直线 AB 与 CD 所成角的大小为 2arccos .4 （ III ） 解 ： 设 平 面 ACD 的 法 向 量 为 ( , , ),n x y z 则 . ( , , ).( 1,0, 1) 0, . ( , , ).(0, 3, 1) 0, n AD x y z n AC x y z             0, 3 0. x z y z     令 1,y  得 ( 3,1, 3)n   是平面 ACD 的一个法向量。 又 1 3( , ,0),2 2EC   点 E 到平面 ACD 的距离 . 3 21 .77 EC n h n       （19）本小题主要考查函数、导数及其应用等基本知识，考查运用数学知识分析和解决实际 问题的能力。满分 12 分。 解：（I）当 40x  时，汽车从甲地到乙地行驶了100 2.540  小时， 要耗没 31 3( 40 40 8) 2.5 17.5128000 80       （升）。 答：当汽车以 40 千米/小时的速度匀速行驶时，从甲地到乙地耗油 17.5 升。 （II）当速度为 x 千米/小时时，汽车从甲地到乙地行驶了100 x 小时，设耗油量为 ( )h x 升， 依题意得 3 21 3 100 1 800 15( ) ( 8). (0 120),128000 80 1280 4h x x x x xx x         3 3 2 2 800 80'( ) (0 120).640 640 x xh x xx x      令 '( ) 0,h x  得 80.x  当 (0,80)x 时， '( ) 0, ( )h x h x 是减函数； 当 (80,120)x 时， '( ) 0, ( )h x h x 是增函数。 x C A B O D y z E 当 80x  时， ( )h x 取到极小值 (80) 11.25.h  因为 ( )h x 在 (0,120] 上只有一个极值，所以它是最小值。 答：当汽车以 80 千米/小时的速度匀速行驶时，从甲地到乙地耗油最少，最少为 11.25 升。 （20）本小题主要考查直线、圆、椭圆和不等式等基本知识，考查平面解析几何的基本方法， 考查运算能力和综合解题能力。满分 12 分。 解：（I） 2 22, 1, 1, ( 1,0), : 2.a b c F l x       圆过点 O、F， 圆心 M 在直线 1 2x   上。 设 1( , ),2M t 则圆半径 1 3( ) ( 2) .2 2r      由 ,OM r 得 2 21 3( ) ,2 2t   解得 2.t   所求圆的方程为 2 21 9( ) ( 2) .2 4x y    （II）设直线 AB 的方程为 ( 1)( 0),y k x k   代入 2 2 1,2 x y  整理得 2 2 2 2(1 2 ) 4 2 2 0.k x k x k     直线 AB 过椭圆的左焦点 F，方程有两个不等实根。 记 1 1 2 2( , ), ( , ),A x y B x y AB 中点 0 0( , ),N x y 则 2 1 2 2 4 ,2 1 kx x k     AB 的垂直平分线 NG 的方程为 0 0 1 ( ).y y x xk     令 0,y  得 2 2 2 0 0 2 2 2 2 2 1 1 .2 1 2 1 2 1 2 4 2 10, 0,2 G G k k kx x ky k k k k k x                  点 G 横坐标的取值范围为 1( ,0).2  （21）本小题主要考查函数的单调性、极值、最值等基本知识，考查运用导数研究函数性质 的方法，考查运算能力，考查函数与方程、数形结合、分类与整合等数学思想方法和分析问 题、解决问题的能力。满分 12 分。 解：（I） 2 2( ) 8 ( 4) 16.f x x x x       当 1 4,t   即 3t  时， ( )f x 在 , 1t t  上单调递增， 2 2( ) ( 1) ( 1) 8( 1) 6 7;h t f t t t t t           当 4 1,t t   即3 4t  时， ( ) (4) 16;h t f  当 4t  时， ( )f x 在 , 1t t  上单调递减， 2( ) ( ) 8 .h t f t t t    综上， 2 2 6 7, 3, ( ) 16, 3 4, 8 , 4 t t t h t t t t t           　　　　 　　 （II）函数 ( )y f x 的图象与 ( )y g x 的图象有且只有三个不同的交点，即函数 ( ) ( ) ( )x g x f x   的图象与 x 轴的正半轴有且只有三个不同的交点。 2 2 ( ) 8 6ln , 6 2 8 6 2( 1)( 3)'( ) 2 8 ( 0), x x x x m x x x xx x xx x x                  当 (0,1)x 时， '( ) 0, ( )x x  是增函数； 当 (0,3)x 时， '( ) 0, ( )x x  是减函数； 当 (3, )x  时， '( ) 0, ( )x x  是增函数； 当 1,x  或 3x  时， '( ) 0.x  ( ) (1) 7, ( ) (3) 6ln3 15.x m x m          最大值 最小值 当 x 充分接近 0 时， ( ) 0,x  当 x 充分大时， ( ) 0.x  要使 ( )x 的图象与 x 轴正半轴有三个不同的交点，必须且只须 ( ) 7 0, ( ) 6ln3 15 0, x m x m          最大值 最小值 即 7 15 6ln3.m   所以存在实数 m ，使得函数 ( )y f x 与 ( )y g x 的图象有且只有三个不同的交点，m 的取值范围为 (7,15 6ln3). （22）本小题主要考查数列、不等式等基本知识，考查化归的数学思想方法，考查综合解题 能力。满分 14 分。 （I）解： * 1 2 1( ),n na a n N    1 1 2( 1),n na a     1na  是以 1 1 2a   为首项，2 为公比的等比数列。 1 2 .n na   即 2 *2 1( ).na n N   （II）证法一： 1 2 11 14 4 ...4 ( 1) .n nk kk k na    1 2( ... )4 2 .n nk k k n nk     1 22[( ... ) ] ,n nb b b n nb      ① 1 2 1 12[( ... ) ( 1)] ( 1) .n n nb b b b n n b         ② ②－①，得 1 12( 1) ( 1) ,n n nb n b nb     即 1( 1) 2 0,n nn b nb    2 1( 1) 2 0.n nnb n b     ③－④，得 2 12 0,n n nnb nb nb    即 2 12 0,n n nb b b    * 2 1 1 ( ),n n n nb b b b n N        nb 是等差数列。 证法二：同证法一，得 1( 1) 2 0n nn b nb    令 1,n  得 1 2.b  设 2 2 ( ),b d d R   下面用数学归纳法证明 2 ( 1) .nb n d   （1）当 1,2n  时，等式成立。 （2）假设当 ( 2)n k k  时， 2 ( 1) ,kb k d   那么 1 2 2[2 ( 1) ] 2 [( 1) 1] .1 1 1 1k k k kb b k d k dk k k k              这就是说，当 1n k  时，等式也成立。 根据（1）和（2），可知 2 ( 1)nb n d   对任何 *n N 都成立。  1 ,n n nb b d b    是等差数列。 （III）证明： 1 1 2 1 2 1 1 , 1,2,..., ,12 1 22(2 )2 k k k k kk a k na         1 2 2 3 1 ... .2 n n aa a n a a a       1 1 1 2 1 1 1 1 1 1 1 1. , 1,2,..., ,2 1 2 2(2 1) 2 3.2 2 2 2 3 2 k k k k k k k k a k na               1 2 2 2 3 1 1 1 1 1 1 1 1... ( ... ) (1 ) ,2 3 2 2 2 2 3 2 2 3 n n n n aa a n n n a a a                *1 2 2 3 1 1 ... ( ).2 3 2 n n aa an n n Na a a         