新教材数学人教B版必修第二册课件：6-2-4　向量的数量积 44页

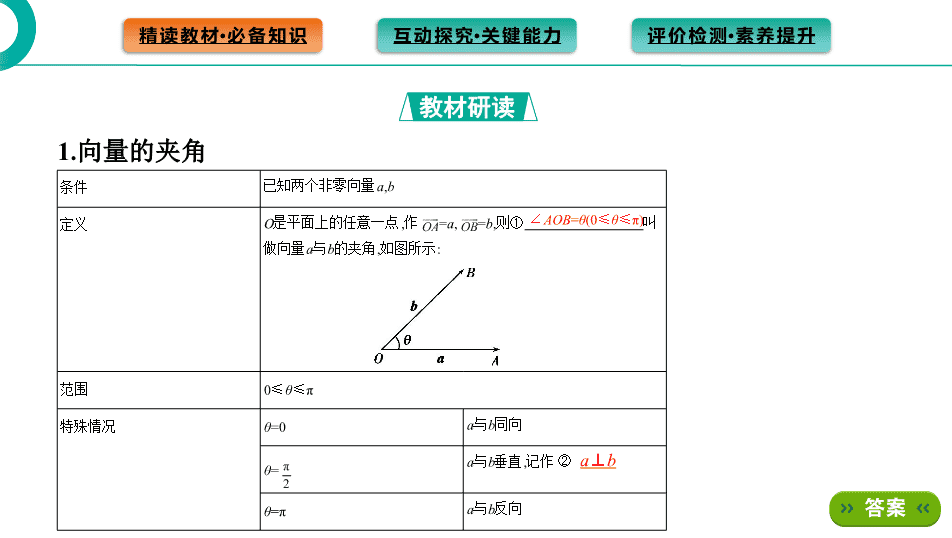
精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 第六章　平面向量及其应用 §6.2　平面向量的运算 6.2.4　向量的数量积 第 一 篇 教 材 过 关 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 一天,物理课上刚学完“做功”这部分内容,小明气喘吁吁地跑进教室,说帮别 人抬东西了,太重了,累得不轻,同学说他又没有做功,不要喊累,于是他们争吵 了起来…… 问题1:小明和同学谁说得对呢? 情景导学 精读教材·必备知识 答案　从物理的角度说小明没有做功,而从日常生活中说小明确实做功了. 问题2:从数学的角度能解释这个问题吗? 答案　能. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 1.向量的夹角 教材研读 条件 已知两个非零向量a,b 定义 O是平面上的任意一点,作  =a,  =b,则① 叫 做向量a与b的夹角,如图所示:   范围 0≤θ≤π 特殊情况 θ=0 a与b同向 θ=  a与b垂直,记作 ② θ=π a与b反向 OA  OB  π 2 ∠AOB=θ(0≤θ≤π) a⊥b 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 提示　两个向量共起点. 思考1:计算向量的夹角时,两个向量需满足什么条件? 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 2.向量的数量积 条件 两个非零向量a与b,它们的夹角为θ 定义 数量|a||b|cos θ叫做向量a与b的数量积(或内积) 记法 a·b=③ 规定 0与任一向量的数量积为0 |a||b|cos θ 思考2:向量的数量积与数乘向量的区别是什么? 提示　向量的数量积是一个实数,不考虑方向,只有大小,而数乘向量是一个向 量,既有大小,又有方向. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 3.投影向量 如图1,设a,b是两个非零向量,  =a,  =b,我们考虑如下的变换:过  的起点A 和终点B,分别作  所在直线的垂线,垂足分别为A1,B1,得到  ,我们称上述变 换为向量a向向量b④ ,  叫做向量a在向量b上的⑤ .   AB  CD  AB  CD  1 1A B  1 1A B 投影 投影向量 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 如图2,我们可以在平面内任取一点O,作  =a,  =b,过点M作直线ON的 垂线,垂足为M1,则  就是向量a在向量b上的投影向量. 思考3:向量b在向量a上的投影与向量a在向量b上的投影分别是什么? OM  ON  1OM  提示　向量a在向量b上的投影是|a|cos θ =  ·b,向量b在向量a上的投影是|b| cos θ =  ·a. | | b b 2 a b b  | | a a 2 a b a  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 4.平面向量数量积的性质 设a,b是两个非零向量,它们的夹角是θ,e是与b方向相同的单位向量,则 (1)a·e=e·a=|a|cos θ. (2)a⊥b⇔ a·b=0. (3)当a与b同向时,a·b=⑥ ; 当a与b反向时,a·b=⑦ . 特别地,a·a=|a|2或|a|=  . 此外,由|cos θ|≤1还可以得到 a a |a||b| -|a||b| 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 (4)|a·b|≤⑧ . (5)cos θ=  (其中θ是非零向量a与b的夹角). 思考4:|a·b|≤|a||b|的等号什么时候成立? | || | a b a b  |a||b| 提示　当且仅当向量a,b共线,即a∥b时,等号成立. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 5.数量积的运算律 已知向量a,b,c和实数λ,则 (1)交换律:a·b=b·a; (2)数乘结合律:(λa)·b=λ(b·a)=a·(λb); (3)分配律:(a+b)·c=⑨ . 思考5:(a·b)·c=a·(b·c)成立吗? a·c+b·c 提示　不成立.因为(a·b)·c表示一个与c共线的向量,而a·(b·c)表示一个与a共线 的向量,若c与a不共线,只有a·b=b·c=0时才相等. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究一　数量积的运算 互动探究·关键能力 例1　(1)已知|a|=2,|b|=3,a与b的夹角为120°,则(a+b)·(a-b)=　　　 ,(2a-b)·(a+ 3b)=　　　 . (2)在Rt△ABC中,∠C=90°,AB=5,AC=4,求  ·  .AB  AC  -5 -34 解析　(1)(a+b)·(a-b)=a2-a·b+a·b-b2=a2-b2=|a|2-|b|2=4-9=-5. (2a-b)·(a+3b)=2a2+6a·b-a·b-3b2=2|a|2+5a·b-3|b|2=2×4-5×3-3×9=-34. (2)  ·  =|  ||  |cos∠BAC=5×4× =16. AB  AC  AB  AC  4 5 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 思维突破 向量数量积的求法 (1)确定两个向量的模及两个向量的夹角,其中确定夹角是求数量积的关键. (2)向量数量积的运算类似于多项式的乘法运算,要根据数量积的运算律计算. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 跟踪训练 1-1　在△ABC中,M是BC的中点,AM=3,BC=10,则  ·  =　　　 .AB  AC  -16 解析　设∠AMB=θ,则∠AMC=π-θ, ∵  =  -  ,  =  -  , ∴  ·  =(  -  )·(  -  )=  ·  -  ·  -  ·  +  =-25-5×3cos θ-3× 5cos(π-θ)+9=-16.   AB  MB  MA  AC  MC  MA  AB  AC  MB  MA  MC  MA  MB  MC  MB  MA  MA  MC  2MA  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 1-2　如图,在平行四边形ABCD中,已知|  |=4,|  |=3,∠DAB=60°,求: (1)  ·  ; (2)  ·  ; (3)  ·  .   AB  AD  AD  BC  AB  CD  AB  DA  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　(1)∵  与  平行且方向相同,∴  与  的夹角为0°, ∴  ·  =|  ||  |cos 0°=3×3×1=9. (2)  与  平行且方向相反, ∴  与  的夹角是180°, ∴  ·  =|  ||  |cos 180°=4×4×(-1)=-16. (3)∵  与  的夹角是60°, ∴  与  的夹角是120°, ∴  ·  =|  ||  |cos 120°=4×3×  =-6. AD  BC  AD  BC  AD  BC  AD  BC  AB  CD  AB  CD  AB  CD  AB  CD  AB  AD  AB  DA  AB  DA  AB  DA  1- 2      精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究二　与模、夹角有关的问题 例2　(1)(易错题)已知|a|=|b|=5,向量a、b的夹角θ= ,则|a+b|=　　　 . (2)已知a,b是两个非零向量,且|a|=|b|=|a-b|,则a与a+b的夹角为　　　　 . π 3 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　(1)a·b=|a||b|cos θ=5×5×cos  = . |a+b|=  =  =  =5  . (2)∵|a|=|a-b|, π 3 25 2 2( )a b 2 2| | 2 | |a a b b  2525 2 252    3 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 ∴|a|2=|a-b|2=|a|2-2a·b+|b|2. 又|a|=|b|,∴a·b= |a|2, 又|a+b|=  =  =  |a|, 设a与a+b的夹角为θ, 则cos θ=  =  =  = , 又θ∈[0,π],∴θ= , 1 2 2( )a b 2 2| | 2 | |a a b b  3 ( ) | || | a a b a a b    2 | || | a a b a a b   2 21| | | |2 | | 3| | a a a a  3 2 π 6 即a与a+b的夹角为 .π 6 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 易错点拨 错误地类比实数运算中的法则,实际上 |a2-b2|=|(a+b)·(a-b)|≤|a+b||a-b|. 1.利用数量积求解长度问题: (1)a2=a·a=|a|2或|a|=  . (2)|a±b|2=(a±b)2=a2±2a·b+b2. 求模一般转化为求模的平方. a a 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 2.求向量的夹角的步骤: (1)求a·b及|a||b|,有时可结合数量积的定义或性质进行计算; (2)利用cos θ=  求出cos θ的值; (3)借助θ∈[0,π],求出θ. | || | a b a b  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 跟踪训练 2-1　已知向量a,b的夹角为60°,且|a|=2,|b|=1,若c=2a-b,d=a+2b,则c·d= 　　 ,|c+2d|=　　 　 .9 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　因为向量a与b的夹角为60°, |a|=2,|b|=1. 所以a·b=|a||b|cos 60°=1. c·d=(2a-b)·(a+2b)=2a2+3a·b-2b2=2|a|2+3×1-2|b|2=2×22+3-2×12=9. 因为c+2d=(2a-b)+2(a+2b)=4a+3b, |c+2d|2=(c+2d)2=(4a+3b)2=16a2+24a·b+9b2 =16|a|2+24×1+9|b|2=16×22+24×1+9×1=97, 所以|c+2d|=  .97 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 2-2　已知|a|=2,|b|=1,a与b的夹角为60°,则向量m=2a+b与向量n=a-4b的夹角的 余弦值为　　 　 . 解析 a·b=2×1×cos 60°=1, |m|2=|2a+b|2=4|a|2+4a·b+|b|2=4×22+4×1+1=21, |n|2=|a-4b|2=|a|2-8a·b+16|b|2=22-8×1+16×1=12, ∴|m|=  ,|n|=2  , 21 3 m·n=(2a+b)·(a-4b)=2|a|2-7a·b-4|b|2=2×22-7×1-4×1=-3. 设m,n的夹角为θ,则cos θ=  =  =- .| || | m n m n  -3 21 2 3 7 14 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究三　两向量的垂直问题 例3　(1)已知两个单位向量a与b的夹角为60°,若a+λb与λa+b互相垂直,则λ的取 值范围是　　　 . (2)已知向量a,b不共线,且|2a+b|=|a+2b|,求证:(a+b)⊥(a-b). 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　(1)∵两个单位向量a与b的夹角为60°, ∴a·b=|a||b|cos 60°=1×1×cos 60°= , 又a+λb与λa+b互相垂直, ∴(a+λb)·(λa+b)=0, ∴λa2+(λ2+1)a·b+λb2=0, ∴λ2+4λ+1=0, 1 2 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 ∴λ∈{-2-  ,-2+  }. (2)证明:∵|2a+b|=|a+2b|, ∴(2a+b)2=(a+2b)2, ∴4a2+4a·b+b2=a2+4a·b+4b2, ∴a2=b2, 3 3 ∴(a+b)·(a-b)=a2-b2=0. 又a与b不共线,∴a+b≠0,a-b≠0, ∴(a+b)⊥(a-b). 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 思维突破 两向量垂直的作用 (1)根据a·b=0可证明向量a与b垂直; (2)向量a与b垂直,则a·b=0,可列方程(组)求未知数; (3)利用两向量垂直可解(或证明)平面几何图形中的垂直问题. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 跟踪训练 3-1　已知e1与e2是两个互相垂直的单位向量,若向量e1+ke2与ke1+e2的夹角为锐 角,则k的取值范围为　　　　　 .(0,1)∪(1,+∞) 解析　∵e1+ke2与ke1+e2的夹角为锐角, ∴(e1+ke2)·(ke1+e2)=k +k +(k2+1)·e1·e2=2k>0, ∴k>0.当k=1时,e1+ke2=ke1+e2, 它们的夹角为0,不符合题意,舍去. 综上,k的取值范围为(0,1)∪(1,+∞). 2 1e 2 2e 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 3-2　已知非零向量a,b满足a+3b与7a-5b互相垂直,a-4b与7a-2b互相垂直,求a与 b的夹角. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　由已知条件得   即  ( 3 ) (7 -5 ) 0, ( -4 ) (7 -2 ) 0, a b a b a b a b       2 2 2 2 7 16 -15 0, 7 -30 8 0, a a b b a a b b         ① ② ②-①得,23b2-46a·b=0, ∴2a·b=b2,代入①得a2=b2, ∴|a|=|b|,∴cos θ=  = = . ∵θ∈[0,π],∴θ= . | || | a b a b  2 2 1 2 | | b b 1 2 π 3 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 探究四　向量的投影 例4　如图所示,在△ABC中,AB=AC=4,∠BAC=90°,D是BC边的中点. 求:(1)  在  上的投影向量; (2)  在  上的投影向量.   AB  BD  BD  AB  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　如图所示,连接AD,因为AB=AC=4,∠BAC=90°,所以△ABC是等腰直角 三角形,又D是BC边的中点,所以AD⊥BC,∠ABD=45°,所以BD=2  . 延长AB到E,则  与  的夹角为∠DBE=180°-45°=135°.   (1)  在  上的投影向量为|  |cos 135°·  =4×  ×  =-  . 2 AB  BD  AB  BD  AB  | | BD BD   2- 2       2 2 BD  BD  (2)  在  上的投影向量为|  |cos 135°·  =2  ×  × =- .BD  AB  BD  | | AB AB   2 2- 2       4 AB  2 AB  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 思维突破 设向量a与b的夹角为θ,则a在b上的投影向量为|a|cos θ ,b在a上的投影向量为 |b|cos θ ,注意区分两者之间的差异. | | b b | | a a 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 跟踪训练 4-1　已知向量a,b的夹角为120°,且|a|=1,|b|=2,则向量a+b在向量a上的投影向 量是　　　 .0 解析　∵向量a,b的夹角为120°, 且|a|=1,|b|=2, ∴(a+b)·a=a2+a·b=12+1×2×cos 120°=0, ∴向量a+b在向量a上的投影向量是0. 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 1.设e1,e2是两个平行的单位向量,则下列选项中正确的是  (　 　) A.e1·e2=1　 B.e1·e2=-1 C.|e1·e2|=1　 D.|e1·e2|<1 课堂检测 评价检测·素养提升 解析　设e1与e2的夹角为θ,则e1·e2=|e1|·|e2|cos θ=±1,所以|e1·e2|=1. C 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 2.已知非零向量a,b,若a+2b与a-2b互相垂直,则 =  (　　 ) A. 　 B.4　 C. 　 D.2 | | | | a b 1 4 1 2 解析　∵(a+2b)·(a-2b)=a2-4b2=0, ∴|a|=2|b|,∴ =2.| | | | a b D 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 3.在△ABC中,若  ·  +  =0,则  在  上的投影向量为(　 　) A.  　 B.   C.  　 D.   AB  BC  2 AB  BC  BA  BA  1 2 AB  AC  1 2 CA  解析　∵0=  ·  +  =  ·(  +  )=  ·  ,∴  ⊥  ,∴  与  的 夹角为锐角,∴  在  上的投影向量为  . AB  BC  2 AB  AB  BC  AB  AB  AC  AB  AC  BC  BA  BC  BA  BA  A 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 4.若|a|=1,|b|=2,c=a+b,且c⊥a,则向量a与b的夹角为  (　　) A.30°　 B.60°　 C.120°　 D.150° 解析　设向量a,b的夹角为θ. 由题意得a·c=a·(a+b)=|a|2+|a|·|b|cos θ=0, 所以cos θ=- .又θ∈[0,π],所以向量a,b的夹角为120°.1 2 C 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 5.已知向量a与b的夹角为45°,且|a|=1,|2a+b|=  ,求|b|. 10 解析　因为|2a+b|=  , 所以(2a+b)2=10, 所以4a2+4a·b+b2=10, 又因为向量a与b的夹角为45°,且|a|=1, 所以4×12+4×1×|b|× +|b|2=10, 整理,得|b|2+2  |b|-6=0, 解得|b|=  或|b|=-3  (舍去). 10 2 2 2 2 2 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 逻辑推理——利用向量判断三角形形状 在△ABC中,  =c,  =a,  =b,且a·b=b·c=c·a,试判断△ABC的形状.AB  BC  CA  素养演练 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析　在△ABC中,易知  +  +  =0, 即a+b+c=0, 因此a+b=-c,a+c=-b, 从而    AB  BC  CA  2 2 2 2 ( ) (- ) , ( ) (- ) , a b c a c b       2 2 2 2 2 2 2 , 2 , a b a b c a c a c b           精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 两式相减可得b2+2a·b-c2-2a·c=c2-b2, 则2b2+2(a·b-a·c)=2c2, 因为a·b=a·c, 所以2b2=2c2,即|b|=|c|. 同理可得|a|=|b|,故|  |=|  |=|  |, 即△ABC是等边三角形. 素养探究:解题的关键是利用a+b+c=0,对数据进行整理、转化,利用方程思想 可得到a、b、c中两个向量的长度之间的关系,过程中体现逻辑推理核心素养. AB  BC  CA  精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 针对训练 　若O是△ABC所在平面内一点,且满足|  -  |=|  +  -2  |,则△ABC的形 状为  (　　) A.等腰直角三角形　 B.直角三角形 C.等腰三角形　 D.等边三角形 OB  OC  OB  OC  OA  B 精读教材·必备知识 互动探究·关键能力 评价检测·素养提升 解析   +  -2  =  -  +  -  =  +  ,  -  =  =  -  , 又|  -  |=|  +  -2  |,所以|  -  |=|  +  |, 所以|  -  |2=|  +  |2,即  ·  =0, 所以AB⊥AC.故△ABC为直角三角形. OB  OC  OA  OB  OA  OC  OA  AB  AC  OB  OC  CB  AB  AC  OB  OC  OB  OC  OA  AB  AC  AB  AC  AB  AC  AB  AC  AB  AC 