备战2014高考数学 高频考点归类分析（真题为例）：函数图象的交点 3页

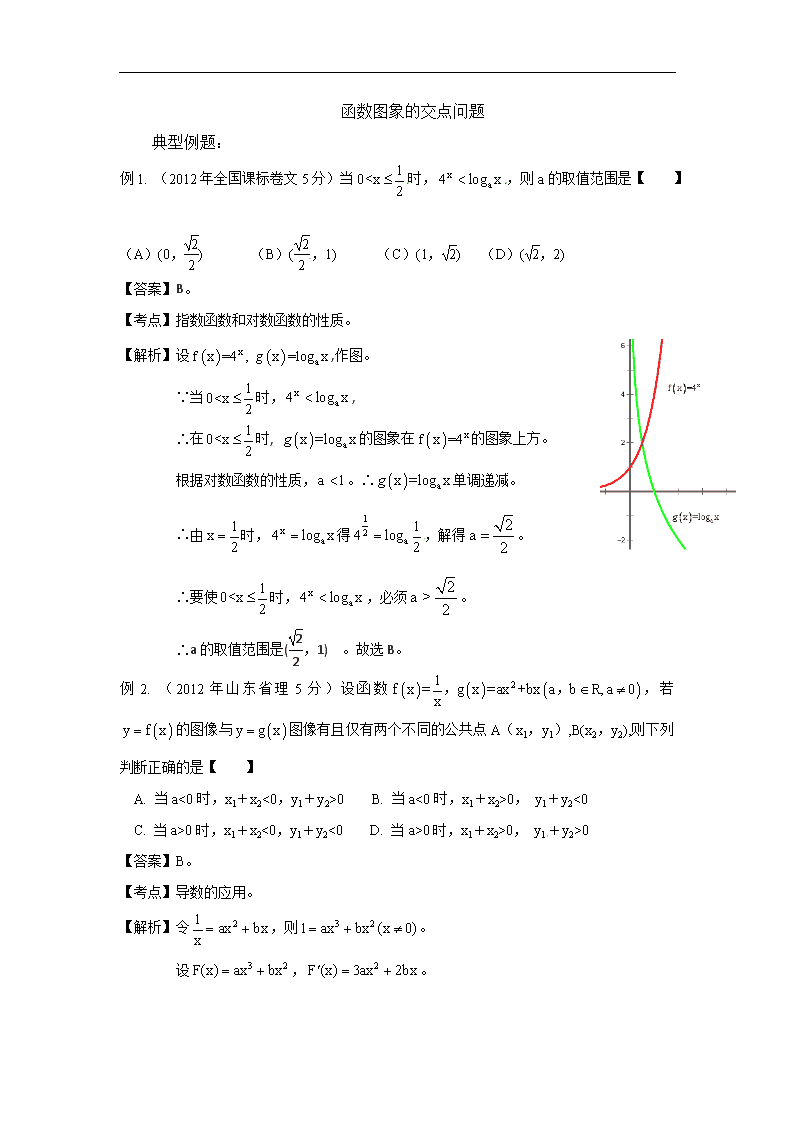
函数图象的交点问题 典型例题： ‎ 例1. （2012年全国课标卷文5分）当时，，则a的取值范围是【 】 [来源:学科网ZXXK][来源:学科网]‎ ‎（A）(0，) （B）(，1) （C）(1，) （D）(，2)‎ ‎【答案】B。‎ ‎【考点】指数函数和对数函数的性质。‎ ‎【解析】设,作图。[来源:学科网]‎ ‎ ∵当时，, ‎ ‎∴在时, 的图象在的图象上方。‎ ‎　　　 根据对数函数的性质，。∴单调递减。‎ ‎ ∴由时，得，解得。‎ ‎ ∴要使时，，必须。‎ ‎ ∴a的取值范围是(，1) 。故选B。‎ 例2. （2012年山东省理5分）设函数，若的图像与图像有且仅有两个不同的公共点A（x1，y1）,B(x2，y2),则下列判断正确的是【 】‎ A. 当a<0时，x1＋x2<0，y1＋y2>0 B. 当a<0时，x1＋x2>0， y1＋y2<0‎ C. 当a>0时，x1＋x2<0，y1＋y2<0 D. 当a>0时，x1＋x2>0， y1＋y2>0‎ ‎【答案】B。‎ ‎【考点】导数的应用。‎ ‎【解析】令，则。‎ 设，。‎ 令，则[来源:Z+xx+k.Com]‎ 要使的图像与图像有且仅有两个不同的公共点必须：‎ ‎，整理得。‎ 取值讨论：可取来研究。‎ 当时，，解得，此时，此时；‎ 当时，，解得，此时，此时。故选B。‎ 例3. （2012年天津市理5分）已知函数的图象与函数的图象恰有两个交点，则实数的取值范围是 ▲ .‎ ‎【答案】。‎ ‎【考点】函数的图像及其性质，利用函数图像确定两函数的交点。‎ ‎【分析】函数，‎ 当时，，‎ 当时，，[来源:学科网ZXXK]‎ 综上函数。‎ 作出函数的图象，要使函数与有两个不同的交点，则直线必须在蓝色或黄色区域内，如图，此时当直线经过黄色区域时，满足，当经过蓝色区域时，满足，综上实数的取值范围是。‎ 例4. （2012年福建省理4分）对于实数a和b，定义运算“*”：a*b＝设，且关于x的方程恰有三个互不相等的实数根x1，x2，x3，则x1x2x3的取值范围是 ▲ ．‎ ‎【答案】。‎ ‎【考点】新定义，分段函数的图象和性质，分类讨论和数形结合思想的应用。‎ ‎【解析】根据新运算符号得到函数为，‎ ‎ 化简得：。‎ 如图，作出函数和的图象，‎ 如果有三个不同的实数解，即直线与函数f(x)的图象有三个交点，如图，‎ ‎（1）当直线过抛物线的顶点或时，有两个交点；‎ ‎（2）当直线中时，有一个交点；‎ ‎（3）当直线中时，有三个交点。‎ 设三个交点分别为：x1，x2，x3，且依次是从小到大的顺序排列，所以x1即为方程2x2－x＝小于0的解，解得x1＝，此时x2＝x3＝，所以x1·x2·x3＝××＝。‎ 与函数f(x)有2个交点的最低位置是当y＝m与x轴重合时，此时x1·x2·x3＝0。‎ 所以当方程有三个不等实根时，x1·x2·x3∈。‎