- 440.09 KB
- 2021-04-16 发布
第十七章 勾股定理
17.1 勾股定理
知识点 勾股定理
1955年希腊发行了一张邮票,图案是由三个棋盘排列而成的.这张
邮票是纪念2500年前希腊一个学术和宗教团体——毕达哥拉斯
学派,它的成立以及在文化上的黄页,我们通过数格子的方法很容
易发现直角三角形三边之间的关系.
知识点 勾股定理的验证
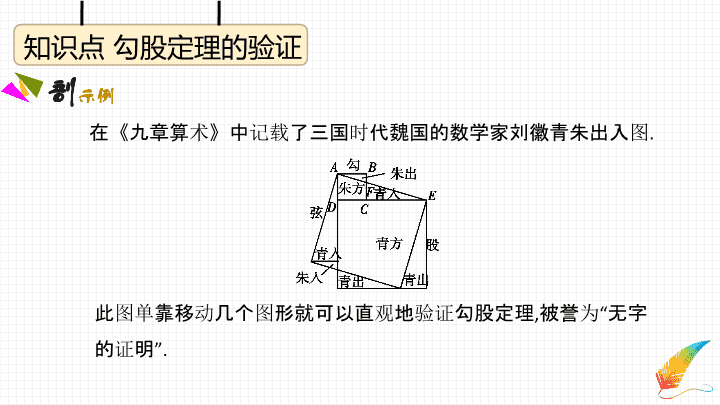
在《九章算术》中记载了三国时代魏国的数学家刘徽青朱出入图.
此图单靠移动几个图形就可以直观地验证勾股定理,被誉为“无字
的证明”.
知识点 勾股定理在实际问题中的应用
少数人为了避开草地的拐角走“捷径”,他们仅仅就是为了少走几步
路(图中4 m),在草地内走出了一条“路”,却踩伤了草,三条路就组成
了直角三角形.
知识点 作长为 (n为大于1的整数)的线段
“勾股海螺”
知识点 作长为 (n为大于1的整数)的线段
作一条长度等于无理数的线段方法不唯一,尽量利用直角边长为整
数的直角三角形作出.另外要注意:并不是所有的无理数都能用尺
规作图的方法在数轴上作出对应的点,如π,0.1010010001……(相邻
两个1之间0的个数逐次加1)等.
第十七章 勾股定理
17.2 勾股定理的逆定理
知识点 互逆命题与互逆定理
公元前6世纪,古希腊哲人泰勒斯利用影子测量了金字塔的高度,他
自己还发现了三角形的一个特征:等腰三角形的两个底角相等,反
过来说,要使三角形两角相等,它们的对边必须相等.这个发现我们
现在看起来很简单,可是在当时发现它们的确不易,其实这两个三
角形的特征是互逆命题,或者说是互逆定理.
知识点 勾股定理的逆定理
古埃及人画直角的方法:把一根长绳打上等距离的13个结,然后以3
个结间距、4个结间距、5个结间距的长度为边长,用木桩就可以钉
成一个直角三角形.此三边的关系就可以判定直角三角形.
知识点 勾股数
神奇的三个台球号码,不但是连续的整数,还是一组勾股数.
您可能关注的文档
相关文档
- 八年级下数学课件《用反比例函数解2021-04-15 23:20:2717页
- 八年级下数学课件《可能性的大小》2021-04-15 23:18:3518页
- 八年级下数学课件《三角形的中位线2021-04-15 21:52:4217页
- 八年级下数学课件《二次根式》 (2021-04-15 21:18:1913页
- 八年级下数学课件:16-1 二次根式—2021-04-15 17:51:2720页
- 八年级下数学课件19-3《坐标与图形2021-04-15 17:50:2419页
- 八年级下数学课件《普查与抽样调查2021-04-15 16:30:3219页
- 八年级下数学课件八年级下册数学课2021-04-15 16:03:2220页
- 八年级下数学课件:17-2 勾股定理的2021-04-15 15:43:2313页
- 八年级下数学课件八年级下册数学课2021-04-15 15:38:0514页