2020届高考理科数学二轮专题复习课件：专题4 立体几何2-4-解答题 2 71页

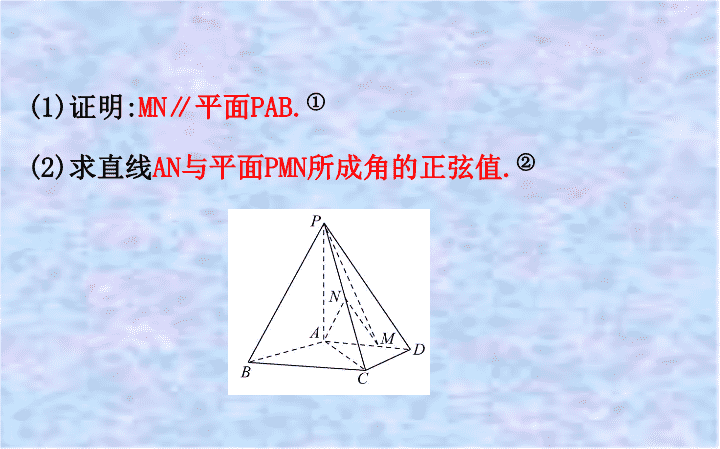
第 2 课时　 空间角、空间距离的计算问题 考向一　利用空间向量计算空间角 角度 1 　　求线面角或异面直线所成的角 【例 1 】 (2016· 全国卷 Ⅲ) 如图 , 四棱锥 P-ABCD 中 ,PA⊥ 底面 ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M 为线段 AD 上一点 ,AM=2MD,N 为 PC 的中点 . (1) 证明 : MN∥ 平面 PAB. ① (2) 求直线 AN 与平面 PMN 所成角的正弦值 . ② 【题眼直击】 题眼 思维导引 ① 想到在平面 PAB 内找到一条直线与 MN 平行 ② 作出线面角 , 利用向量法求线面角 【解析】 (1) 由已知得 AM= AD=2, 取 BP 的中点 T, 连接 AT,TN, 由 N 为 PC 中点知 TN∥BC,TN= BC=2. 又 AD∥BC, 故 TN∥AM,TN=AM, 四边形 AMNT 为平行四边形 , 于是 MN∥AT. 因为 AT⊂ 平面 PAB,MN⊄ 平面 PAB, 所以 MN∥ 平面 PAB. (2) 取 BC 的中点 F, 连接 AF. 由 AB=AC 得 AF⊥BC, 从而 AF⊥AD 且 以 A 为坐标原点 , 的方向为 x 轴的正方向 , 的方向 为 y 轴的正方向 , 的方向为 z 轴的正方向 , 建立空间 直角坐标系 , 由题意可得 所以 设 n =(x,y,z) 为平面 PMN 的法向量 , 则 即 可取 n = 所以 cos < n , >= 所以直线 AN 与平面 PMN 所成角的正弦值为 【拓展提升】 求线面角的常用方法 (1) 找 : 即找出直线与平面所成的角 , 再通过解三角形求解 , 具体步骤为 : ① 寻找过斜线上一点与平面垂直的直线 , 或过斜线上一点作平面的垂线 , 确定垂足的位置 ; ② 连接垂足和斜足得到斜线在平面内的射影 , 斜线与其射影所成的锐角或直角即为所求的角 ; ③ 将该角归结为某个三角形的内角 ( 一般是直角三角形 ), 通过解三角形 ( 可能需要解多个三角形 ) 求得该角或其三角函数值 . (2) 算 :① 几何法 :sin θ= . 其中 ,θ 为线面角 ,h 为点 B 到平面 α 的距离 , l 为斜线段 AB 的长 . ② 空间向量法 . 【变式训练】 将边长为 1 的正方形 AA 1 O 1 O( 及其内部 ) 绕 OO 1 旋转一周形 成圆柱 , 如图 , 长为 长为 其中 B 1 与 C 在 平面 AA 1 O 1 O 的同侧 . (1) 求三棱锥 C-O 1 A 1 B 1 的体积 . (2) 求异面直线 B 1 C 与 AA 1 所成的角的大小 . 【解析】 (1) 连接 A 1 B 1 , 因为 所以 ∠ O 1 A 1 B 1 =∠A 1 O 1 B 1 = 所以△ O 1 A 1 B 1 为正三角形 , 所以 所以 所以三棱锥 C-O 1 A 1 B 1 的体积为 (2) 以 O 为坐标原点建立空间直角坐标系如图 , 则 A(0,1,0),A 1 (0,1,1), 所以 =(0,0,1), =(0,-1,-1), 所以 所以 所以异面直线 B 1 C 与 AA 1 所成的角为 角度 2 　二面角的计算 【例 2 】 (2019· 全国卷 Ⅰ) 如图 , 直四棱柱 ABCD-A 1 B 1 C 1 D 1 的底面是菱形 ,AA 1 =4,AB=2,∠BAD=60°, E,M,N 分别是 BC,BB 1 ,A 1 D 的中点 . 世纪金榜导学号 (1) 证明 : MN∥ 平面 C 1 DE. ① (2) 求二面角 A-MA 1 -N 的正弦值 . ② 【题眼直击】 题眼 思维导引 ① 想到线面平行的判定定理 ② 建立空间直角坐标系 , 利用向量法求二面角的正弦值 【解析】 (1) 连接 B 1 C,ME. 因为 M,E 分别为 BB 1 ,BC 的中点 , 所以 ME∥B 1 C, 且 ME= B 1 C. 又因为 N 为 A 1 D 的中点 , 所以 ND= A 1 D. 由题设知 A 1 B 1