- 1.83 MB
- 2021-05-11 发布
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角
第四课时 圆周角及其定理
§ 知识点1 圆周角
§ 顶点在圆上,并且两边都与圆相交的
角,叫做圆周角.
§ 如图,点A、B、C、D、E都是⊙ O
上的点,则∠ABC,∠ACB,∠BAC,
∠ACD,∠BCD,∠CDE都是圆周
角.
2
注意:判断一个角是否是圆周角,关键看两点:①角的顶点是否在圆上;②
角的两边是否分别与圆相交.两个条件,缺一不可.
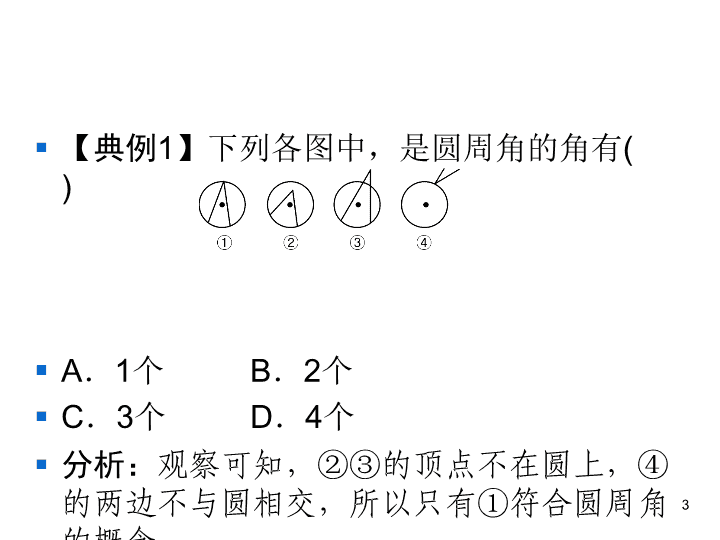
§ 【典例1】下列各图中,是圆周角的角有(
)
§ A.1个 B.2个
§ C.3个 D.4个
§ 分析:观察可知,②③的顶点不在圆上,④
的两边不与圆相交,所以只有①符合圆周角
的概念.
§ 答案:A
3
§ 知识点2 圆周角定理及其推论
§ 定理:一条弧所对的圆周角等于它所对的圆
心角的一半.
§ 推论:(1)同弧或等弧所对的圆周角相等;
§ (2)半圆(或直径)所对的圆周角是直角,90°
的圆周角所对的弦是直径.
§ 核心提示:圆中常作的辅助线:有直径,常
作出直径所对的圆周角,这个圆周角是直
角. 4
§ 【典例2】如图,已知⊙ O是△ABD的外接圆,
AB是⊙ O的直径,CD是⊙ O的弦,∠ABD=
58°,则∠BCD等于( )
§ A.16°
§ B.32°
§ C.58°
§ D.64°
§ 分析:因为AB是⊙O的直径,所以∠ADB=
90°,所以∠A=90°-∠ABD=32°,所
以∠BCD=∠A=32°.
§ 答案:B
5
§ 【典例3】如图,OA、OB是⊙ O
的半径且OA⊥OB,作OA的垂直
平分线交⊙ O于点C、D,连接CB、
AB.求证:∠ABC=2∠CBO.
6
7
§ 1.下列图形中的角,是圆心角的个数是
( )
§ A.1 B.2
§ C.3 D.4 8
B
§ 2.【2018·辽宁阜新中考】如图,AB是⊙ O
的直径,点C在圆上,∠ABC=65°,那么
∠OCA的度数是 ( )
§ A.25° B.35°
§ C.15° D.20°
9
A
10
D
§ 4.如图,点A、B、C、P在⊙ O上,
CD⊥OA,CE⊥OB,垂足分别为点D、E,
∠DCE=40°,则∠P的度数为 ( )
§ A.140° B.70°
§ C.60° D.40°
11
B
§ 5.如图,已知AB=AC=AD,∠CBD=
2∠BDC,∠BAC=44°,则∠CAD的度数
为 ( )
§ A.68° B.88°
§ C.90° D.112° 12
B
13
D
§ 7.某小区新建一个圆形人工湖,如图所示,
弦AB是湖上一座桥,已知桥AB长为200 m,
测得圆周角∠ACB=45°,则这个人工湖的
直径AD长为_________m.
14
15
§ 9.如图,△ABC的3个顶点都在⊙ O上,直
径AD=2,∠ABC=30°,则AC=_____.
16
1
17
70°
§ 11.如图,△ABC内接于⊙ O,BC
=4,CA=3,∠A-∠B=90°,
求⊙ O的半径.
18
19
§ 13.如图,△ABC内接于⊙ O,
AM平分∠BAC交⊙ O于点M,
AD⊥BC于点D.求证:∠MAO=
∠MAD.
20
证明:延长AO交⊙O于点N,连接BN.∵AN是⊙O的直径,
AD⊥BC,∴∠ABN=∠ADC=90°,∴∠BAN+∠N=90°,
∠DAC+∠C=90°.∵∠N=∠C,∴∠BAN=∠DAC.∵AM平分
∠BAC,∴∠BAM=∠CAM,∴∠MAO=∠MAD.
21
22
23
相关文档
- 2020春六年级语文下册第六单元难忘2021-05-11 03:28:4328页
- 【部编人教版】六上语文18《只有一2021-05-11 03:16:4848页
- 2020春六年级语文下册古诗词诵读课2021-05-11 02:55:1739页
- (课堂教学课件2)金木水火土2021-05-11 02:10:5715页
- 部编版 小学一年级下册语文(课堂教2021-05-11 01:59:1922页
- 部编版三年级上册语文作文(课堂教学2021-05-10 23:17:5331页
- 部编版 小学一年级下册语文(·课堂2021-05-10 22:13:578页
- 部编版 小学一年级下册语文(·课堂2021-05-10 19:38:3310页
- 统编版二年级语文上册-(课堂教学课2021-05-10 19:11:4111页
- 部编版 小学一年级下册语文(·课堂2021-05-10 18:55:0823页