八年级下数学课件《三角形的中位线》 (10)_苏科版 13页

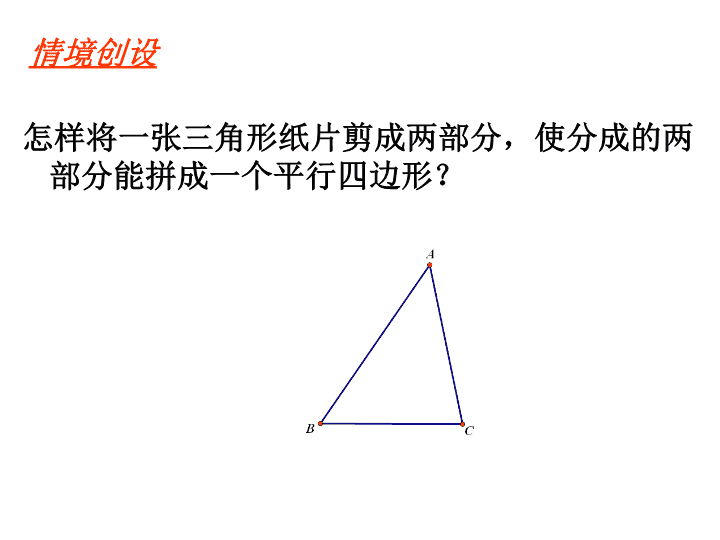
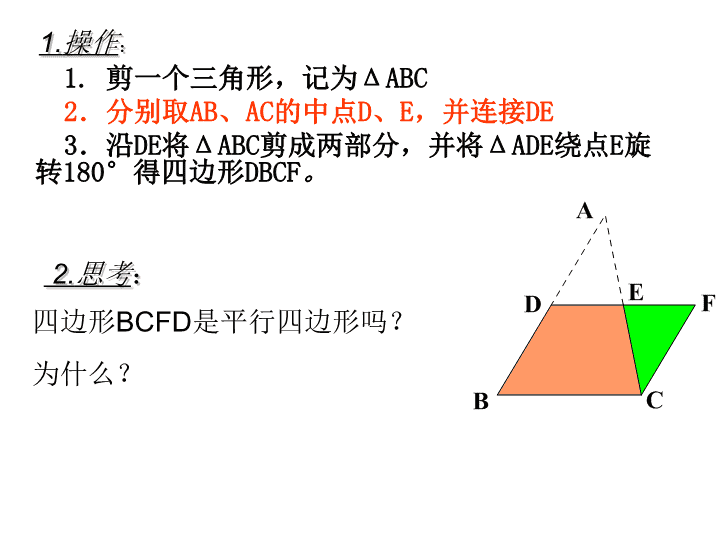
9.5 三角形的中位线 情境创设 怎样将一张三角形纸片剪成两部分，使分成的两 部分能拼成一个平行四边形？ 1. 剪一个三角形，记为ΔABC 2．分别取AB、AC的中点D、E，并连接DE 3．沿DE将ΔABC剪成两部分，并将ΔADE绕点E旋 转180°得四边形DBCF。 1.操作： 2.思考： A B C D E F四边形BCFD是平行四边形吗？ 为什么？ 三角形中位线的概念　 连接三角形两边的中点的线段叫做三角形的中位线 1.三角形的中位线与三角形的中线的区别是什么？　 想一想： 2.请分别画出△ABC的所有中线， △ABC的所有中位线。 3.定义： 议一议： ΔABC的中位线DE与第三边BC有怎样的位置和数量 关系？为什么？ ↓ ↓ 位置关系 数量关系 ∵DE为ΔABC的中位线 ∴DE∥BC，DE=½BC A B C D E F 三角形中位线的性质: 三角形的中位线平行于第三边，并且等于第 三边的一半。 数学实验室： 1.准备好一张直角三角形的纸片，将该三角形按图1方式折 叠并展开。 （1）非重叠部分是等腰三角形吗？为什么？ （2）折痕是原三角形的中位线吗？说说你的理由。 2.准备好一张任意的锐角三角形纸片如图2，你可以折出它 的一条中位线吗？你有不同的折法吗？ （1）如图，在△ABC中，AB=8，点D,E分别是 BC,CA的中点，连接DE，则DE=______。4 （2）如图ΔABC中，AB=6㎝， AC=8㎝，BC=10 ㎝，D﹑E﹑F分别是AB、AC、BC的中点，则 ΔDEF的周长是 ，面积是 . 12cm 6cm2 对于任意ΔABC，它的中位线三 角形ΔDEF满足如下关系： ΔDEF的周长等于ΔABC的_______ ΔDEF的面积等于ΔABC的_______ 1 4 1 2 例 题 ： 如图，四边形ABCD中，E F G H分别是AB CD AD BC的中点， 四边形EFGH是平行四边形吗？为什么？ 解：四边形EFGH是平行四边形 连接DB ∵ E、H分别是AB、AD的中点 ， ∴ EH是ΔABD的中位线 ∴ EH∥BD，EH=½ BD，理由是：三角形的中位线平行 于第三边，并且等于它的一半。 同理可得，FG∥BD FG=½BD ∴ EH∥FG，EH=FG ∴ 四边形EFGH是平行四边形 1.在四边形ABCD中，AC=BD，E、F、G、H 分别是AB、BC、CD、DA的中点. 求证：四边形EFGH是菱形 2.如果将 AC = BD 换为AC ⊥ BD 四边形EFGH是什么形状？ 3.若换为 AC = BD 且AC ⊥ BD呢？ 议一议： 1.当四边形的对角线________时，顺次连接它的四边中点所 得的四边形是菱形. 相等 互相垂直 互相垂直且相等 2.当四边形的对角线__________时，顺次连接它的四边中点所 得的四边形是矩形. 3.当四边形的对角线_______________时，顺次连接它的四边 中点所得的四边形是正方形. 课后检测 　已知：如图，在四边形ABCD中，AB＝CD，E、 F、G分别是BD、AC、BC的中点． 　　求证：△EFG是等腰三角形． A B C D E F G H 如果H是AD的中点，连接EH、FH 求证：四边形EGFH是菱形。 本课小结 １.理解三角形中位线的概念：连接三角形两 边的中点的线段叫做三角形的中位线。 ２.掌握三角形中位线的性质：三角形的中位线 平行与第三边，并且等于它的一半。 3．能应用三角形中位线的性质解决有关计算或 说理等问题。