数学华东师大版九年级上册教案24-3 锐角三角函数 第2课时 3页

1 24.3 锐角三角函数 第 2 课时 教学目标 1．经历探索 30°、45°、60°角的三角函数值的过程，进一步体会三角函数的意义； 2．能够进行 30°、45°、60°角的三角函数值的计算； 3．能够结合 30°、45°、60°的三角函数值解决简单实际问题． 教学重难点 【教学重点】 30°、45°、60°角的三角函数值. 【教学难点】 结合 30°、45°、60°的三角函数值解决简单实际问题. 课前准备 无 教学过程 一、情境导入 问题 1：一个直角三角形中，一个锐角的正弦、余弦、正切值是怎么定义的？ 问题 2：两块三角尺中有几个不同的锐角？各是多少度？设每个三角尺较短的边长为 1，分 别求出这几个锐角的正弦值、余弦值和正切值． 二、合作探究 探究点一：特殊角的三角函数值 【类型一】 利用特殊的三角函数值进行计算 计算： (1)2cos60°·sin30°－ 6sin45°·sin60°； (2)sin30°－sin45° cos60°＋cos45° . 解析：将特殊角的三角函数值代入求解． 解：(1)原式＝2×1 2 ×1 2 － 6× 2 2 × 3 2 ＝1 2 －3 2 ＝－1； (2)原式＝ 1 2 － 2 2 1 2 ＋ 2 2 ＝2 2－3. 方法总结： 解决此类题目的关键是熟记特殊角的三角函数值． 【类型二】 已知三角函数值求角的取值范围 若 cosα＝2 3 ，则锐角α的大致范围是( ) A．0°＜α＜30° B．30°＜α＜45° C．45°＜α＜60° D．0°＜α＜30° 2 解析：∵cos30°＝ 3 2 ，cos45°＝ 2 2 ，cos60°＝1 2 ，且1 2 ＜2 3 ＜ 2 2 ，∴cos60°＜cosα＜ cos45°，∴锐角α的范围是 45°＜α＜60°.故选 C. 方法总结：解决此类问题要熟记特殊角的三角函数值和三角函数的增减性． 【类型三】 根据三角函数值求角度 若 3tan(α＋10°)＝1，则锐角α的度数是( ) A．20° B．30° C．40° D．50° 解析：∵ 3tan(α＋10°)＝1，∴tan(α＋10°)＝ 3 3 .∵tan30°＝ 3 3 ，∴α＋10°＝30°， ∴α＝20°.故选 A. 方法总结：熟记特殊角的三角函数值是解决问题的关键． 探究点二：特殊角的三角函数值的应用 【类型一】 利用三角形的边角关系求线段的长 如图，在△ABC 中，∠ABC＝90°，∠A＝30°，D 是边 AB 上一点，∠BDC＝45°，AD ＝4，求 BC 的长． 解析：由题意可知△BCD 为等腰直角三角形，则 BD＝BC，在 Rt△ABC 中，利用锐角三角函数 的定义求出 BC 的长即可． 解：∵∠B＝90°，∠BDC＝45°，∴△BCD 为等腰直角三角形，∴BD＝BC.在 Rt△ABC 中， tan∠A＝tan30°＝BC AB ，即 BC BC＋4 ＝ 3 3 ，解得 BC＝2( 3＋1)． 方法总结：在直角三角形中求线段的长，如果有特殊角，可考虑利用三角函数的定义列出式 子，求出三角函数值，进而求出答案． 【类型二】 判断三角形的形状 已知△ABC 中的∠A 与∠B 满足(1－tanA)2＋|sinB－ 3 2 |＝0，试判断△ABC 的形状． 解析：根据非负性的性质求出 tanA 及 sinB 的值，再根据特殊角的三角函数值求出∠A 及∠ B 的度数，进而可得出结论． 解：∵(1－tanA)2＋|sinB－ 3 2 |＝0，∴tanA＝1，sinB＝ 3 2 ，∴∠A＝45°，∠B＝60°， ∠C＝180°－45°－60°＝75°，∴△ABC 是锐角三角形． 方法总结：一个数的绝对值和偶次方都是非负数，当几个数或式的绝对值或偶次方相加和为 0 时，则其中的每一项都必须等于 0. 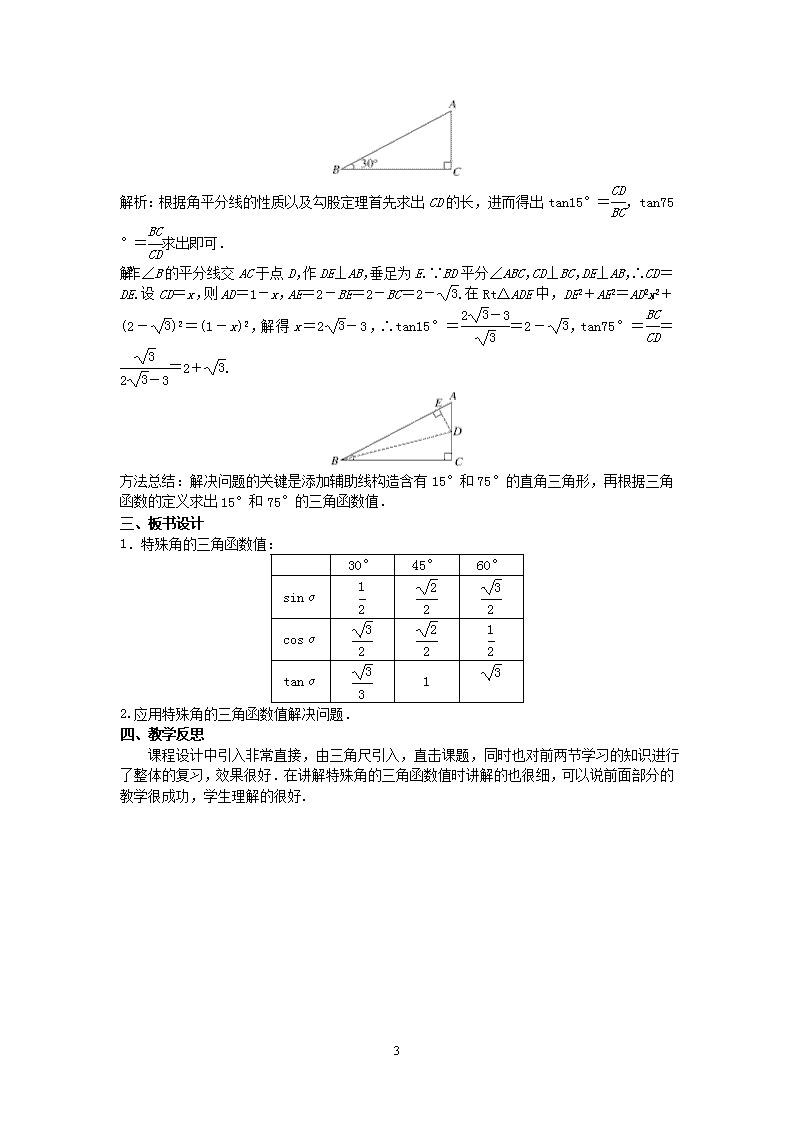【类型三】 构造三角函数模型解决问题 要求 tan30°的值，可构造如图所示的直角三角形进行计算．作 Rt△ABC，使∠C＝90°， 斜边 AB＝2，直角边 AC＝1，那么 BC＝ 3，∠ABC＝30°，∴tan30°＝AC BC ＝ 1 3 ＝ 3 3 .在此图 的基础上，通过添加适当的辅助线，探究 tan15°与 tan75°的值． 3 解析：根据角平分线的性质以及勾股定理首先求出 CD 的长，进而得出 tan15°＝CD BC ，tan75° ＝BC CD 求出即可． 解：作∠B 的平分线交 AC 于点 D，作 DE⊥AB，垂足为 E.∵BD 平分∠ABC，CD⊥BC，DE⊥AB， ∴CD＝DE.设 CD＝x，则 AD＝1－x，AE＝2－BE＝2－BC＝2－ 3.在 Rt△ADE 中，DE2＋AE2＝ AD2，x2＋(2－ 3)2＝(1－x)2，解得 x＝2 3－3，∴tan15°＝2 3－3 3 ＝2－ 3，tan75°＝BC CD ＝ 3 2 3－3 ＝2＋ 3. 方法总结：解决问题的关键是添加辅助线构造含有 15°和 75°的直角三角形，再根据三角 函数的定义求出 15°和 75°的三角函数值． 三、板书设计 1．特殊角的三角函数值： 30° 45° 60° sinα 1 2 2 2 3 2 cosα 3 2 2 2 1 2 tanα 3 3 1 3 2.应用特殊角的三角函数值解决问题． 四、教学反思 课程设计中引入非常直接，由三角尺引入，直击课题，同时也对前两节学习的知识进行 了整体的复习，效果很好．在讲解特殊角的三角函数值时讲解的也很细，可以说前面部分的 教学很成功，学生理解的很好.