- 188.50 KB
- 2021-05-10 发布
复习与回顾:
1.菱形的定义:
2.菱形的性质:
有一组邻边相等的平行
四边形叫做菱形。
菱
形
性
质
边 角 对角线
邻角互补 对边平行
四边相等 对角相等
对角线互相平分、
互相垂直且平分一
组对角
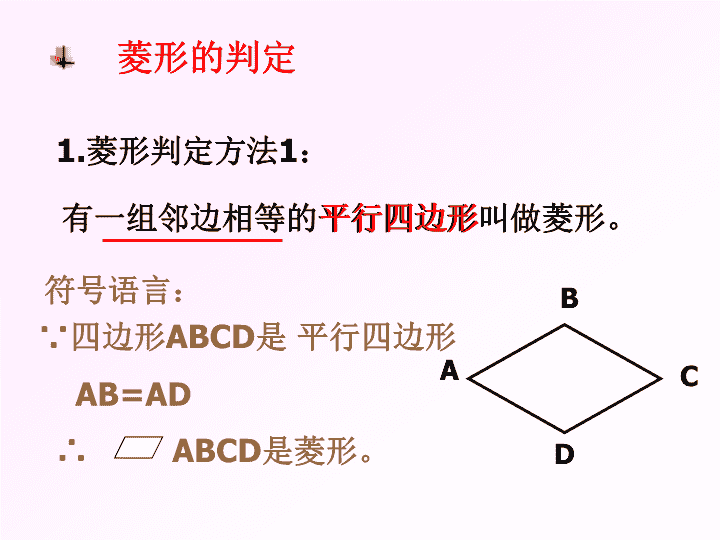
菱形的判定
1.菱形判定方法1:
有一组邻边相等的平行四边形叫做菱形。平行四边形
符号语言:
∵四边形ABCD是 平行四边形
AB=AD
∴ ABCD是菱形。
A
B
C
D
菱形的判定
2.四条边相等的四边形是菱形吗?
已知:四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形。
菱形判定方法2:四条边相等的四边形是菱形
∵AB=BC=CD=DA
∴四边形ABCD是菱形。
符号语言:
A
B
C
D
菱形的判定
3.观察与思考:如图,四边形ABCD的对角线
AC⊥BD,则四边形ABCD是不是菱形?
若 ABCD的对角线AC⊥BD ,则 ABCD是
不是菱形?为什么?
注: 对角线互相垂直的四边形不能判定为菱形。
C
B
D
A
D
CA
B
已知:在 ABCD 中,对角线AC⊥BD
求证: ABCD是菱形。
证明:∵四边形ABCD是平行四边形,
∴OB=OD
又∵AC⊥BD
∴ ABCD是菱形。
∴AB=AD
菱形判定方法3: 对角线互相垂直的平行四边形是菱形。
∵四边形ABCD是平行四边形,
AC⊥BD,
∴ ABCD是菱形。
符号语言:
C
B
D
A O
练习巩固
一.选择:
(一) 的平行四边形是菱形。( )
(二) 的四边形是菱形。 ( )
1.一组邻边相等 2.四条边相等 3.对角线相等
4.对角线相等且互相平分 5.对角线互相垂直
6.对角线互相垂直且平分
1 5
2 6
例题解析:
已知: ABCD的对角线AC的垂直平分
线与边AD 、BC分别交于E、F
求证:四边形AFCE是菱形。
分析: (1)利用定义判定
B
D
CF
EA
O
(2) 由已知可知
OA=OC,EF⊥AC.
(3)利用四边相等,你会吗?
分析:四边形AFCE是菱形
AE=EC=CF=FA
AE=EC AF=CF AE=AF
EF 垂直平分AC ∠1= ∠2
∠1= ∠3 ∠2= ∠3
AE∥FC
四边形ABCD 是平行四边形
AF=CF EF ⊥AC
B
D
CF
EA
O
1
2 3
二.已知:如图,矩形ABCD的对角线
相交于点O,PD∥AC,PC∥BD,PD、
PC相交于点P。
(1)猜想:四边形PCOD是什么
特殊的四边形?
(2)试证明你的猜想。
(3) PO与CD有怎样的关系?
四边形PCOD是菱形。
PO与CD互相垂直且平分
C
A B
O
D
P
一组邻边相等对角线互相垂直
四条边相等
五
种
判
定
方
法
四边形
平行四边形
菱形
菱形的判定方法:
小结:
作业:
1、已知: ABCD的对角线AC的垂直平分线与边AD 、
BC分别交于E、F
求证:四边形AFCE是菱形。
B
D
CF
EA
O
1
2 3
2、已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,
PC∥BD,PD、PC相交于点P。
(1)猜想:四边形PCOD是什么特殊的四边形?
(2)试证明你的猜想。
C
A B
O
D
P
G
E
F
D
C
B A
已知,如图, ∠ ABC中, ∠ ACB=90,BE平分∠ ABC,
CD AB于D,和BF交于点G , GE ∥ CA.
求证:CE和FG互相垂直平分。
2、已知如图,△ABC中AD平分∠BAC,
DE∥AB交AC于F, DF∥AC交AB于E。四
边形AFDE是怎样的四边形?说明你的理由。
43
21
F E
D
CB
A
相关文档
- 八年级下数学课件八年级下册数学课2021-05-10 19:55:438页
- 八年级下数学课件:18-2-2 菱形 (共22021-05-10 18:26:3428页
- 八年级下数学课件《9-7利用相似三2021-05-10 18:17:0520页
- 八年级下数学课件:19-2-2 一次函数2021-05-10 18:13:0117页
- 八年级下数学课件复习导入 生活中2021-05-10 17:17:496页
- 八年级下数学课件《用公式法求解一2021-05-10 16:25:5212页
- 八年级下数学课件《抽样调查》课件2021-05-10 13:07:3013页
- 八年级下数学课件:19 一次函数 复2021-05-10 12:34:5433页
- 八年级下数学课件《统计表、统计图2021-05-10 12:34:1722页
- 八年级下数学课件《分式》 (4)_苏2021-05-10 11:01:1910页