- 1.06 MB
- 2021-05-10 发布
第十单元 算法初步、统计、统计案例
1.编写意图
本单元包括两部分内容,一部分是“算法初步”,另一部分是“统计、统计案例”.
本单元在编写时注意到以下几点:
(1)突出主干知识.对核心知识和常考知识点进行重点设计,对各种基本题型进行了详细阐述.
(2)统计方法的讲解.编写时把各种统计方法的使用放在了首位.
(3)把握基本题型.对各种基本题型进行了详细讲解,目的是帮助 生构建知识体系.
2.教 指导
在复习过程中,要注意以下几个方面:
(1)对算法初步教 的建议.由于试题主要考查程序框图和基本算法语句,因此复习该部分时要抓住以下两点:一是程序框图的三种基本逻辑结构,弄清三种基本逻辑结构的功能和使用方法,结合具体题目掌握一些常见的程序框图题;二是理解基本算法语句,搞清楚条件语句与条件结构的对应关系,循环语句与循环结构的对应关系等.
(2)对统计教 的建议.由于统计涉及的概念很多,教 中教师应引导 生结合具体题目仔细体会概念的含义,使 生通过适当练习, 会如何使用概念解题.统计图表是统计中的主要工具,教 中要使 生掌握从图表中提取有关数据的信息并进行统计推断的方法.
(3)加强运算能力的培养.统计的数据计算较复杂,要注重培养 生良好的运算习惯,通过统计的复习提高运算能力.
3.课时安排
本单元包含4讲、小题必刷卷(十四)和解答必刷卷(六),建议每讲1课时完成,小题必刷卷和解答必刷卷各1课时完成,本单元共需6课时.
第63讲 算法初步
考试说明 1.了解算法的含义、算法的思想.
2.理解程序框图的三种基本逻辑结构:顺序、条件分支、循环.
3.了解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.
考情分析
考点
考查方向
考例
考查热度
算法的
含义
算法的含义
★☆☆
流程图
程序框图:顺序结构、条件结构、循环结构
2017全国卷Ⅰ8,2017全国卷Ⅱ8,2017全国卷Ⅲ7,2016全国卷Ⅱ8,2016全国卷Ⅰ9,2016全国卷Ⅲ7,2015全国卷Ⅰ9,2015全国卷Ⅱ8,2014全国卷Ⅰ7
★★★
基本算
法语句
输入语句、输出语句、赋值语句、条件语句、循环语句
★★☆
真题再现
■ [2017-2013 课标全国真题再现
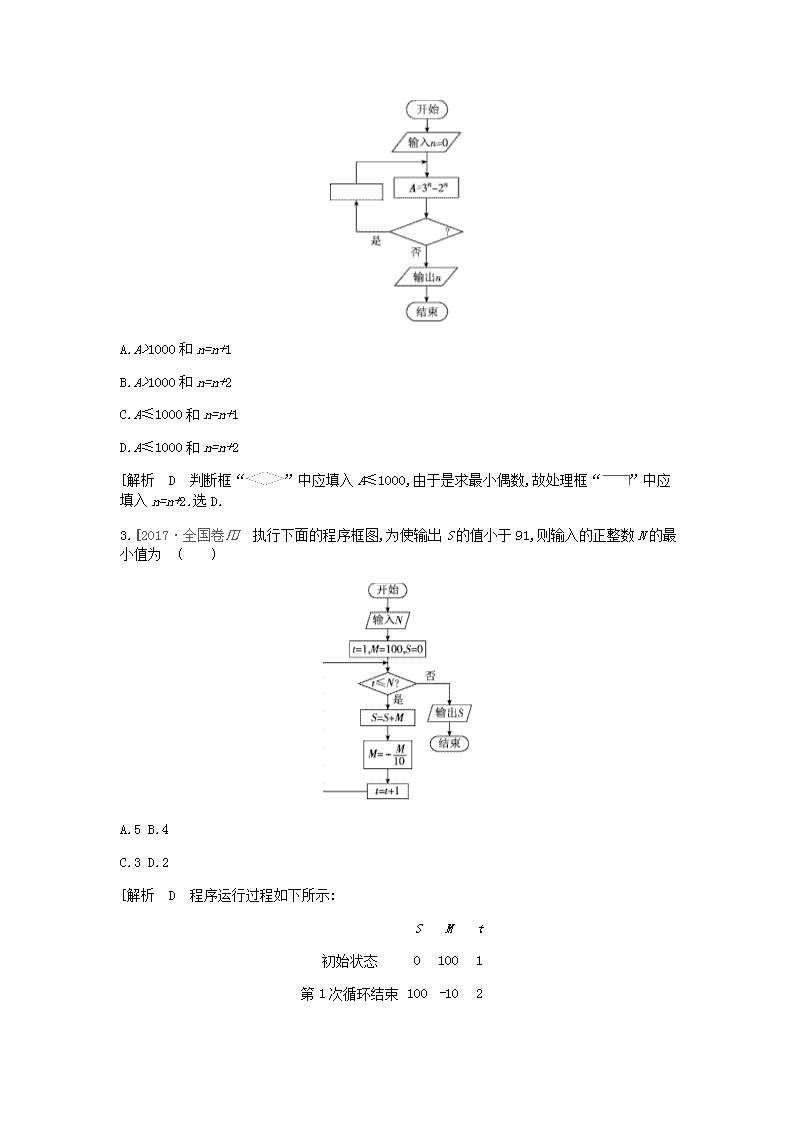
1.[2017·全国卷Ⅱ 执行如图所示的程序框图,如果输入的a=-1,则输出的S= ( )
A.2 B.3
C.4 D.5
[解析 B 逐次计算结果为:S=-1,a=1, =2;S=1,a=-1, =3;S=-2,a=1, =4;S=2,a=-1, =5;S=-3,a=1, =6;S=3,a=-1, =7,此时输出S.故输出的S=3.
2.[2017·全国卷Ⅰ 图的程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在和两个空白框中,可以分别填入 ( )
A.A>1000和n=n+1
B.A>1000和n=n+2
C.A≤1000和n=n+1
D.A≤1000和n=n+2
[解析 D 判断框“”中应填入A≤1000,由于是求最小偶数,故处理框“”中应填入n=n+2.选D.
3.[2017·全国卷Ⅲ 执行下面的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为 ( )
A.5 B.4
C.3 D.2
[解析 D 程序运行过程如下所示:
S
M
t
初始状态
0
100
1
第1次循环结束
100
-10
2
第2次循环结束
90
1
3
此时S=90<91,满足条件,程序需在t=3时跳出循环,即N=2为满足条件的最小值.
4.[2016·全国卷Ⅰ 执行图的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足 ( )
A.y=2x B.y=3x
C.y=4x D.y=5x
[解析 C 第一次运行程序,n=1,x=0,y=1;第二次运行程序,n=2,x=,y=2;第三次运行程序,n=3,x=,y=6,此时满足条件x2+y2≥36,输出x=,y=6,满足y=4x.
5.[2016·全国卷Ⅱ 中国古代有计算多项式值的秦九韶算法,图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s= ( )
A.7 B.12
C.17 D.34
[解析 C 第一次运算,a=2,s=2, =1,不满足 >n;
第二次运算,a=2,s=2×2+2=6, =2,不满足 >n;
第三次运算,a=5,s=6×2+5=17, =3,满足 >n,输出s=17.
6.[2016·全国卷Ⅲ 执行图的程序框图,如果输入的a=4,b=6,那么输出的n= ( )
A.3 B.4
C.5 D.6
[解析 B 当n=1时,s=6;当n=2时,s=10;当n=3时,s=16;当n=4时,s=20,故输出的n=4.
7.[2015·全国卷Ⅰ 执行如图所示的程序框图,如果输入的t=0.01,则输出的n= ( )
A.5 B.6
C.7 D.8
[解析 C 逐次写出循环过程:S=1-=,m=,n=1,S>0.01;S=-=,m=,n=2,S>0.01;S=-=,m=,n=3,S>0.01;S=-
=,m=,n=4,S>0.01;S=-=,m=,n=5,S>0.01;S=-=,m=,n=6,S>0.01;S=-=,m=,n=7,S<0.01,循环结束.故输出的n值为7.
8.[2015·全国卷Ⅱ 如图所示的程序框图的算法思路源于我国古代数 名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a= ( )
A.0 B.2
C.4 D.14
[解析 B 逐一写出循环:a=14,b=18→a=14,b=4→a=10,b=4→a=6,b=4→a=2,b=4→a=2,b=2,结束循环.故选B.
9.[2014·全国卷Ⅰ 执行如图所示的程序框图,若输入的a,b, 分别为1,2,3,则输出的M= ( )
A. B.
C. D.
[解析 D 逐次计算,依次可得:M=,a=2,b=,n=2;M=,a=,b=,n=3;M=,a=,b=,n=4.此时输出M,故输出的是.
■ [2017-2016 其他省份类似高考真题
1.[2017·天津卷 阅读图所示的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为 ( )
A.0 B.1
C.2 D.3
[解析 C 输入N=24,第一次执行N=8;第二次执行N=7;第三次执行N=6;第四次执行N=2,满足条件,输出2.故选C.
2.[2017·山东卷 执行两次图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为 ( )
A.0,0 B.1,1
C.0,1 D.1,0
[解析 D 当x=7时,b=2,此时4<7,且x不能被2整除,所以此时b=3,又因为32>7成立,所以输出a=1;当x=9时,b=2,此时4<9,且x不能被2整除,所以此时b=3,又因为32>9不成立,且x能被3整除,所以输出a=0.故选D.
3.[2017·北京卷 执行如图所示的程序框图,输出的s值为 ( )
A.2 B.
C. D.
[解析 C =0,s=1,满足 <3; =1,s==2,满足 <3; =2,s==,满足 <3; =3,s==,不满足 <3.故输出s=,故选C.
4.[2017·江苏卷 图是一个算法流程图.若输入x的值为,则输出y的值是 .
[答案 -2
[解析 因为输入x的值为,不满足x≥1,所以y=2+log2=-2.
5.[2016·天津卷 阅读如图所示的程序框图,运行相应的程序,则输出S的值为 ( )
A.2 B.4
C.6 D.8
[解析 B 第一次执行循环体后S=8,n=2;第二次执行循环体后S=2,n=3;第三次执行循环体后S=4,n=4,满足n>3,结束循环.故输出S=4.
6.[2016·北京卷 执行如图所示的程序框图,若输入的a值为1,则输出的 值为 ( )
A.1 B.2
C.3 D.4
[解析 B 输入a=1,当 =0时,b=1,a=-,不满足a=b;当 =1时,a=-2,不满足a=b;当 =2时,a=1,满足a=b,结束循环,输出的 值是2.
7.[2016·山东卷 执行如图所示的程序框图,若输入的a,b的值分别为0和9,则输出的i的值为 .
[答案 3
[解析 当i=1时,a=1,b=8;当i=2时,a=3,b=6;当i=3时,a=6,b=3,满足条件.故输出i的值为3.
【课前双基巩固】
知识聚焦
1.(1)一定规则 明确 有限 (2)程序
2.程序框 文字说明
3.依次执行 基本结构 条件是否成立 反复执行 循环体
4.(1)输入信息 变量=表达式
(2)①IF 条件 THEN END IF
②IF 条件 THEN ELSE
(3)①DO LOOP UNTIL ②WHILE WEND
对点演练
1.84 [解析 程序运行过程如下:x=2,S=0;S=22=4,x=2×2=4;S=4+42=20,x=2×4=8;S=20+82=84>64,循环结束,输出S=84.
2.3或-3 [解析 该程序是求函数y=|x|的函数值,∵y=3,∴x=±3.
3.7 [解析 由程序框图可以看出,当n=8>6时,程序结束,故输出S=[ +[ +[ +[ +[ =7.
4.是 否 [解析 当x≥60时,应输出“及格”;当x<60时,应输出“不及格”.故①处应填“是”,②处应填“否”.
5.17 [解析 第一次循环得,a=153-119=34;第二次循环得,b=119-34=85;第三次循环得,b=85-34=51;第四次循环得,b=51-34=17;第五次循环得,a=34-17=17,此时a=b,输出a=17.
【课堂考点探究】
例1 [思路点拨 (1)该程序框图为条件结构,考查分段函数的输出值;(2)列举出循环情况,确定循环终止的条件.
(1)B (2)D [解析 (1)因为-1≤x≤4,所以当-1≤x≤1时,y∈[-1,0 ;当18?”.
变式题 (1)B (2)B [解析 (1)第一次,S=1+21=3,i=1+1=2;第二次,S=3+22=7,i=2+1=3;第三次,S=7+23=15,i=3+1=4;第四次,S=15+24=31,i=4+1=5.输出31,所以判断框中可以填入的条件为“i≤4?”.
(2)在运行程序过程中,p, 的值依次为p=1, =1;p=3, =2;p=12, =3;p=60, =4;p=360,此时不满足 3时收取的费用,结合收费办法可得y=10+[x-3+0.5 ×2+1=2[x+0.5 +5.故选B.
例4 [思路点拨 根据程序框图,依次列举出每次循环的结果,最后转化为数列的求和问题,采用裂项相消法求和即可.
C [解析 模拟程序框图运行过程,如下:
i=1,S=,满足循环条件;
i=2,S=+,满足循环条件;
i=3,S=++,满足循环条件;
i=4,S=+++,不满足循环条件.
此时S=+++=1-+-+-+-=1-=.
强化演练
1.D [解析 运行程序:n=1,s=;n=2,s=+;…;n=1008,s=++…+,结束循环.故输出s=++…+=-+-+…+-=-+-+…+-=1-=.
2.C [解析 由题设中程序框图所提供的算法程序可知:S=1×log2(2+1)=log23, =3;S=log23×log34=2, =4;S=2×log45=2log45, =5;S=2×log45·log56=2log46, =6;S=2×log46·log67=2log47, =7;…;S=2log416=4, =16,不满足循环条件,输出S=4.所以判断框内可能为“ <16?”.
3.B [解析 当n=1时,S=;当n=2时,S=+=;…;当n=4时,S=+++=;当n=5时,S=++++=,此时输出S.故450”,故选A.
变式题 (1)D (2)B [解析 (1)由题意得,该算法的功能是计算y=的函数值,所以,当a=3时,y=6.故选D.
(2)经过第一次循环得到s=1,i=2;经过第二次循环得到s=2,i=3;经过第三次循环得到s=6,i=4;经过第四次循环得到s=24,i=5;经过第五次循环得到s=120,i=6;经过第六次循环得到s=720,i=7,此时,不满足循环的条件,执行输出s.故选B.
【备选理由】例1是茎叶图与程序框图的结合,是对听课正文例2的补充;例2是与函数有关的程序框图问题;例3是与数列有关的程序框图的问题,考查的是对算法功能的理解.
1 [配合例2使用 随机抽取某中 甲、乙两个班各10名同 测量他们的身高,获得身高数据的茎叶图如图①所示,在这20人中,记身高(单位:cm)在[150,160),[160,170),[170,180),[180,190 的人数依次为A1,A2,A3,A4.图②是统计样本中身高在一定范围内的人数的程序框图,若输出的S=18,则判断框内可以填 ( )
A.i<3? B.i≤4?
C.i<4? D.i≤5?
[解析 B 由i的初始值为2,且输出的S=18,可知程序框图的目的是统计身高大于或等于160 cm的人数(恰为18),于是要计算A2+A3+A4的值,因此判断框内可以填“i≤4?”.
2 [配合例3使用 [2017·福州一中质检 下图是用“二分法”求方程近似解的程序框图,在①②处应填写的内容分别是 ( )
A.f(a)·f(m)<0,b=m
B.f(b)·f(m)<0,b=m
C.f(a)·f(m)<0,m=b
D.f(b)·f(m)<0,m=b
[解析 B 因为程序框图的目的是利用“二分法”求方程近似解,所以判断框的内容是根的存在性定理的应用,所以填“f(b)·f(m)<0”,“是”则直接进行验证精度,否则在赋值框中实现b=m的交换,故选B.
3 [配合例4使用 已知程序框图如图所示,则该程序框图的功能是 ( )
A.求数列的前10项和
B.求数列的前10项和
C.求数列的前11项和
D.求数列的前11项和
[解析 B 由题易知当S=++…+时, =11>10,输出S,故选B.