2018-2019学年河南省驻马店市高一下学期期末数学（理）试题（解析版） 17页

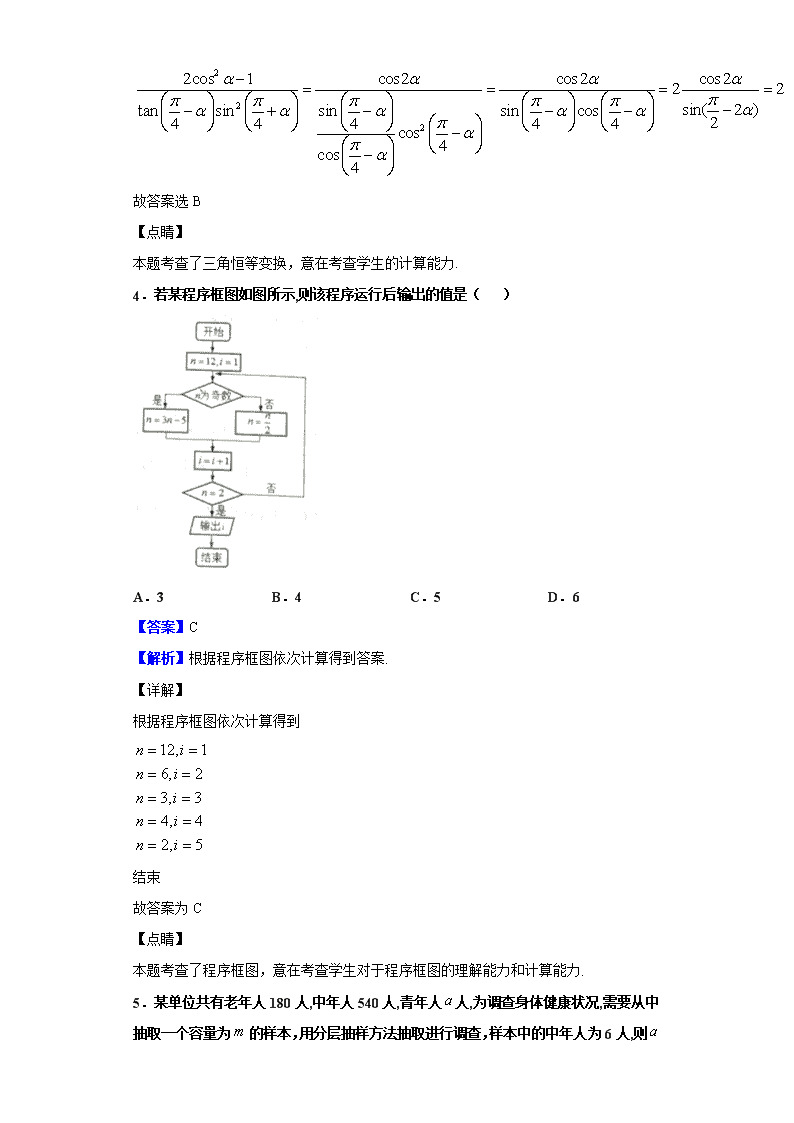
‎2018-2019学年河南省驻马店市高一下学期期末数学（理）试题 一、单选题 ‎1．的值等于( )‎ A． B． C． D．‎ ‎【答案】A ‎【解析】= ,选A.‎ ‎2．已知在中，，且，则的值为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎【解析】先确定D位置，根据向量的三角形法则，将用，表示出来得到答案.‎ ‎【详解】‎ ‎ ‎ 故答案选C ‎【点睛】‎ 本题考查了向量的加减，没有注意向量方向是容易犯的错误.‎ ‎3．计算：的结果为（ ）‎ A．1 B．2 C．-1 D．-2‎ ‎【答案】B ‎【解析】利用恒等变换公式化简得的答案.‎ ‎【详解】‎ 故答案选B ‎【点睛】‎ 本题考查了三角恒等变换，意在考查学生的计算能力.‎ ‎4．若某程序框图如图所示,则该程序运行后输出的值是（ ）‎ A．3 B．4 C．5 D．6‎ ‎【答案】C ‎【解析】根据程序框图依次计算得到答案.‎ ‎【详解】‎ 根据程序框图依次计算得到 ‎ ‎ 结束 故答案为C ‎【点睛】‎ 本题考查了程序框图，意在考查学生对于程序框图的理解能力和计算能力.‎ ‎5．某单位共有老年人180人,中年人540人,青年人人,为调查身体健康状况,需要从中抽取一个容量为的样本，用分层抽样方法抽取进行调查，样本中的中年人为6人,则 和的值不可以是下列四个选项中的哪组（ ）‎ A． B．‎ C． D．‎ ‎【答案】B ‎【解析】根据分层抽样的规律，计算和的关系为： ，将选项代入判断不符合的得到答案.‎ ‎【详解】‎ 某单位共有老年人180人,中年人540人,青年人人,‎ 样本中的中年人为6人，则老年人为： 青年人为： ‎ 代入选项计算，B不符合 故答案为B ‎【点睛】‎ 本题考查了分层抽样，意在考查学生的计算能力.‎ ‎6．已知平面向量满足：，，，若，则的值为（ ）‎ A． B． C．1 D．-1‎ ‎【答案】C ‎【解析】将代入，化简得到答案.‎ ‎【详解】‎ 故答案选C ‎【点睛】‎ 本题考查了向量的运算，意在考查学生的计算能力.‎ ‎7．若直线与函数的图象相邻的两个交点之间的距离为1,则函数图象的对称中心为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】先计算周期得到，得到函数表达式，再根据中心对称公式得到答案.‎ ‎【详解】‎ 直线与函数的图象相邻的两个交点之间的距离为1‎ 则 ‎ 的对称中心横坐标为： ‎ 对称中心为 故答案选A ‎【点睛】‎ 本题考查了函数的周期，对称中心，意在考查学生综合应用能力.‎ ‎8．一组数平均数是，方差是，则另一组数，的平均数和方差分别是（ ）‎ A． B．‎ C． D．‎ ‎【答案】B ‎【解析】直接利用公式：平均值方差为，则的平均值和方差为：得到答案.‎ ‎【详解】‎ 平均数是，方差是 ‎，的平均数为：‎ 方差为：‎ 故答案选B ‎【点睛】‎ 本题考查了平均数和方差的计算：平均数是，方差是，则 的平均值和方差为：.‎ ‎9．已知角满足，，且，，则的值为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】根据角度范围先计算和，再通过展开得到答案.‎ ‎【详解】‎ ‎，‎ ‎，‎ 故答案选D ‎【点睛】‎ 本题考查了三角函数恒等变换，将是解题的关键.‎ ‎10．已知函数的值域为，且图象在同一周期内过两点，则的值分别为（ ）‎ A． B．‎ C． D．‎ ‎【答案】C ‎【解析】根据值域先求，再代入数据得到最大值和最小值对应相差得到答案.‎ ‎【详解】‎ 函数的值域为 即 ‎ ‎，图象在同一周期内过两点 ‎ ‎ 故答案选C ‎【点睛】‎ 本题考查了三角函数的最大值最小值，周期，意在考查学生对于三角函数公式和性质的灵活运用和计算能力.‎ ‎11．在中，已知角的对边分别为，若，，，，且，则的最小角的正切值为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】根据大角对大边判断最小角为，利用正弦定理得到，代入余弦定理计算得到，最后得到.‎ ‎【详解】‎ 根据大角对大边判断最小角为 根据正弦定理知： ‎ 根据余弦定理： ‎ 化简得： ‎ 故答案选D ‎【点睛】‎ 本题考查了正弦定理，余弦定理，意在考查学生的计算能力.‎ ‎12．若关于的方程有两个不同解，则实数的取值范围为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】换元设，将原函数变为，根据函数图像得到答案.‎ ‎【详解】‎ 设，则 ‎，单调递增，则 ‎ 如图：‎ 数的取值范围为 故答案选D ‎【点睛】‎ 本题考查了换元法，参数分离，函数图像，参数分离和换元法可以简化运算，是解题的关键.‎ 二、填空题 ‎13．已知扇形的面积为，圆心角为，则该扇形半径为__________．‎ ‎【答案】2‎ ‎【解析】将圆心角化为弧度制，再利用扇形面积得到答案.‎ ‎【详解】‎ 圆心角为 扇形的面积为 故答案为2‎ ‎【点睛】‎ 本题考查了扇形的面积公式，属于简单题.‎ ‎14．住在同一城市的甲、乙两位合伙人,约定在当天下午4.00-5：00间在某个咖啡馆相见商谈合作事宜，他们约好当其中一人先到后最多等对方10分钟,若等不到则可以离去,则这两人能相见的概率为__________．‎ ‎【答案】‎ ‎【解析】将甲、乙到达时间设为（以为0时刻，单位为分钟）.则相见需要满足： 画出图像，根据几何概型公式得到答案.‎ ‎【详解】‎ 根据题意：将甲、乙到达时间设为（以为0时刻，单位为分钟）‎ 则相见需要满足： 画出图像：‎ 根据几何概型公式：‎ ‎【点睛】‎ 本题考查了几何概型的应用，意在考查学生解决问题的能力.‎ ‎15．在中，已知角的对边分别为，且，，，若有两解，则的取值范围是__________．‎ ‎【答案】‎ ‎【解析】利用正弦定理得到，再根据有两解得到，计算得到答案.‎ ‎【详解】‎ 由正弦定理得： ‎ 若有两解：‎ 故答案为 ‎【点睛】‎ 本题考查了正弦定理，有两解，意在考查学生的计算能力.‎ ‎16．已知当时，函数（‎ 且）取得最小值，则时，的值为__________．‎ ‎【答案】3‎ ‎【解析】先根据计算，化简函数，再根据当时，函数取得最小值，代入计算得到答案.‎ ‎【详解】‎ 或 当时，函数取得最小值：‎ 或（舍去）‎ 故答案为3‎ ‎【点睛】‎ 本题考查了三角函数的化简，辅助角公式，函数的最值，综合性较强，意在考查学生的综合应用能力和计算能力.‎ 三、解答题 ‎17．已知函数，作如下变换：.‎ ‎（1）分别求出函数的对称中心和单调增区间；‎ ‎（2）写出函数的解析式、值域和最小正周期.‎ ‎【答案】（1），；（2），，.‎ ‎【解析】（1）由，直接利用对称中心和增区间公式得到答案.‎ ‎（2）根据变换得到函数的解析式为，再求值域和最小正周期.‎ ‎【详解】‎ 由题意知：（1）‎ 由得对称中心，‎ 由，得：‎ 单调增区间为，‎ ‎（2）所求解析式为：0‎ 值域：‎ 最小正周期：.‎ ‎【点睛】‎ 本题考查了三角函数的对称中心，单调区间，函数变换，周期，值域，综合性强，意在考查学生对于三角函数公式和性质的灵活运用.‎ ‎18．在中，已知角的对边分别为，且.‎ ‎（1）求角的大小；‎ ‎（2）若，是的中点，且，求的面积.‎ ‎【答案】（1）；（2）.‎ ‎【解析】（1）利用正弦定理和和差公式计算得到答案.‎ ‎（2）利用代入余弦定理公式得到，计算面积得到答案.‎ ‎【详解】‎ ‎（1）∵是的内角，‎ ‎∴且 又由正弦定理：和已知条件得：‎ 化简得：，‎ 又∵‎ ‎∴；‎ ‎（2）∵，是的中点，且，，，‎ ‎∴由余弦定理得：，代入化简得：‎ 又，即，可得：‎ 故所求的面积为.‎ ‎【点睛】‎ 本题考查了余弦定理，正弦定理，面积公式，意在考查学生的计算能力.‎ ‎19．为了调查家庭的月收入与月储蓄的情况，某居民区的物业工作人员随机抽取该小区20个家庭，获得第个家庭的月收入（单位：千元）与月储蓄（单位：千元）的数据资料，计算得：，，，，.‎ ‎（1）求家庭的月储蓄对月收入的线性回归方程；‎ ‎（2）指出（1）中所求出方程的系数，并判断变量与之间是正相关还是负相关；‎ ‎（3）若该居民区某家庭月收入为9千元，预测该家庭的月储蓄.‎ ‎【答案】（1）；（2）正相关；（3）2.2千元.‎ ‎【解析】（1）直接利用公式计算回归方程为：.‎ ‎（2）由（1），故正相关.‎ ‎（3）把代入得：.‎ ‎【详解】‎ ‎（1）∵，，样本中心点为：‎ ‎∴由公式得：‎ 把代入得：‎ 所求回归方程为：；‎ ‎（2）由（1）知，所求出方程的系数为：，，‎ ‎∵，‎ ‎∴与之间是正相关.‎ ‎（3）把代入得：（千元）‎ 即该居民区某家庭月收入为9千元时,预测该家庭的月储蓄为2.2千元.‎ ‎【点睛】‎ 本题考查了回归方程的计算和预测，意在考查学生的计算能力.‎ ‎20．已知向量，，.‎ ‎（1）若，求的值；‎ ‎（2）设，若恒成立，求的取值范围.‎ ‎【答案】（1）；（2）.‎ ‎【解析】（1）根据得到计算得到答案.‎ ‎（2）先求出函数表达式为，再求函数的最大值得到答案.‎ ‎【详解】‎ ‎（1）∵，且，，，‎ ‎∴，即，‎ 又∵，∴‎ ‎（2）易知，‎ ‎∵，∴，，‎ 当时，，取得最大值：，‎ 又恒成立，即 故.‎ ‎【点睛】‎ 本题考查了向量平行，函数的最大值，将恒成立问题转化为最值问题是解题的关键.‎ ‎21．驻马店市政府委托市电视台进行“创建森林城市”知识问答活动,市电视台随机对该市15～65岁的人群抽取了人,绘制出如图1所示的频率分布直方图,回答问题的统计结果如表2所示.‎ ‎（1）分别求出的值；‎ ‎（2）从第二、三、四、五组回答正确的人中用分层抽样的方法抽取7人,则从第二、三、四、五组每组回答正确的人中应各抽取多少人?‎ ‎（3）在(2)的条件下,电视台决定在所抽取的7人中随机选2人颁发幸运奖,求所抽取的人中第二组至少有1人获得幸运奖的概率.‎ ‎【答案】（1），，，；（2）2人,3人,1人,1人；（3）.‎ ‎【解析】（1）先计算出总人数为1000人，再根据公式依次计算的值.‎ ‎（2）根据分层抽样规律得到从第二、三、四、五组每组回答正确的人中应分别抽取:2人,3人,1人,1人 ‎（3）排出所有可能和满足条件的情况，得到概率.‎ ‎【详解】‎ ‎（1）依题和图表：‎ 由得：，‎ 由得：，‎ 由得：，‎ 由得：，‎ 由得：，‎ 故所求，，，.‎ ‎（2）由以上知:第二、三、四、五组回答正确的人数分别为:180人,270人,90人,90人 用分层抽样抽取7人,则:‎ 从第二组回答正确的人中应该抽取: 人，‎ 从第三组回答正确的人中应该抽取：人，‎ 从第四组回答正确的人中应该抽取: 人，‎ 从第五组回答正确的人中应该抽取: 人，‎ 故从第二、三、四、五组每组回答正确的人中应分别抽取:2人,3人,1人,1人；‎ ‎（3）设从第二组回答正确的人抽取的2人为: ，‎ 从第三组回答正确的人抽取的3人为: ‎ 从第四组回答正确的人抽取的1人为: ‎ 从第五组回答正确的人抽取的1人为: ‎ 随机抽取2人,所有可能的结果有: ，，，，，，，，，，，，，，，，，，，，，共21个基本事件，其中第二组至少有1人被抽中的有：，，，，，，，，，，共这11个基本事件.‎ 故抽取的人中第二组至少有1人获得幸运奖的概率为：.‎ ‎【点睛】‎ 本题考查了频率直方图，分层抽样，概率的计算，意在考查学生的应用能力和计算能力.‎ ‎22．已知函数.‎ ‎（1）求函数的值域和单调减区间；‎ ‎（2）已知为的三个内角，且，，求的值.‎ ‎【答案】（1），；（2）.‎ ‎【解析】（1）将函数化简，利用三角函数的取值范围的单调性得到答案.‎ ‎（2）通过函数计算，，再计算代入数据得到答案.‎ ‎【详解】‎ ‎（1）∵且 ‎∴故所求值域为 由得：‎ 所求减区间：；‎ ‎（2）∵是的三个内角，，∴‎ ‎∴又，即 又∵，‎ ‎∴,‎ 故,‎ 故.‎ ‎【点睛】‎ 本题考查了三角函数的最值，单调性，角度的大小，意在考查学生对于三角函数公式性质的灵活运用.‎