【物理】2018届二轮复习万有引力定律及其应用学案（全国通用） 4页

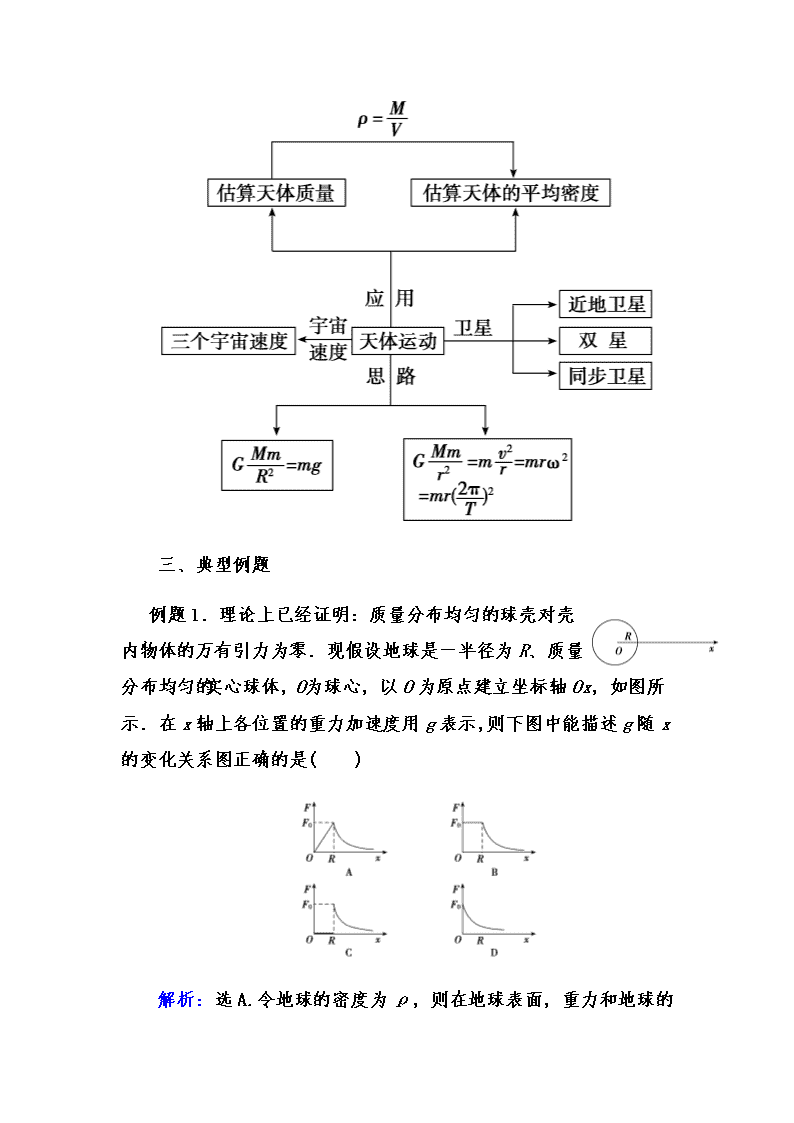
1. 万有引力定律及天体质量和密度的求解 一、基础知识回顾 ‎1．利用天体表面的重力加速度g和天体半径R.‎ 由于G＝mg，故天体质量M＝，天体密度ρ＝＝＝.‎ ‎2．通过观察卫星绕天体做匀速圆周运动的周期T和轨道半径r.‎ ‎(1)由万有引力等于向心力，即G＝mr，得出中心天体质量M＝；‎ ‎(2)若已知天体半径R，则天体的平均密度ρ＝＝＝；‎ ‎(3)若天体的卫星在天体表面附近环绕天体运动，可认为其轨道半径r等于天体半径R，则天体密度ρ＝.可见，只要测出卫星环绕天体表面运动的周期T，就可估算出中心天体的密度．‎ 二、知识网络 三、典型例题 例题1．理论上已经证明：质量分布均匀的球壳对壳内物体的万有引力为零．现假设地球是一半径为R、质量分布均匀的实心球体，O为球心，以O为原点建立坐标轴Ox，如图所示．在x轴上各位置的重力加速度用g表示，则下图中能描述g随x的变化关系图正确的是(　　)‎ 解析：选A.令地球的密度为ρ ‎，则在地球表面，重力和地球的万有引力大小相等，有：g＝ 由于地球的质量为M＝πR3·ρ，所以重力加速度的表达式可写成：g＝.‎ 根据题意有，质量分布均匀的球壳对壳内物体的引力为零，固在深度为h＝R－r的井底，受到地球的万有引力即 为半径等于r的球体在其表面产生的万有引力，g′＝，当r＜R时，g与r成正比，当r＞R后，g与r平方成反比．故选A.‎ 例题2．一卫星绕某一行星表面附近做匀速圆周运动，其角速度大小为ω.假设宇航员登上该行星后，在该行星表面上用弹簧测力计测量一质量为m的物体的重力，物体静止时，弹簧测力计的示数为F0.已知引力常量为G，则这颗行星的质量为(　　)‎ A.　　　　　　　　　 B. C. D. 解析：选A.设行星、卫星的质量分别为M、m卫，行星半径为R，对卫星有G＝m卫ω2R，对质量为m的物体有F0＝G，解以上两式得M＝，A正确．‎ 例题 ‎3．据美国宇航局消息，在距离地球40光年的地方发现了三颗可能适合人类居住的类地行星，假设某天我们可以穿越空间到达某一类地行星，测量以初速度10 m/s竖直上抛一个小球可到达的最大高度只有1 m，而其球体半径只有地球的一半，则其平均密度和地球的平均密度之比为(g＝10 m/s2)(　　)‎ A．5∶2　　　　　　　　 B．2∶5‎ C．1∶10 D．10∶1‎ 解析：选D.根据h＝和g＝可得，M＝即ρπR3＝，行星平均密度ρ＝∝.在地球表面以初速度10 m/s竖直上抛一个小球可到达的最大高度h地＝＝5 m．据此可得，该类地行星和地球的平均密度之比为10∶1，选项D正确．‎