- 709.45 KB
- 2021-05-08 发布
2020届高中毕业班第四次模拟考试试题
理科数学
(答卷时间:120分钟满分:150分)
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷为第1页至第2页.第IⅡ卷为第3页至第4页.
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则
A. B. C. D.
2.若为实数,复数在复平面上位于第四象限,且,则
A. B. C.1 D.2
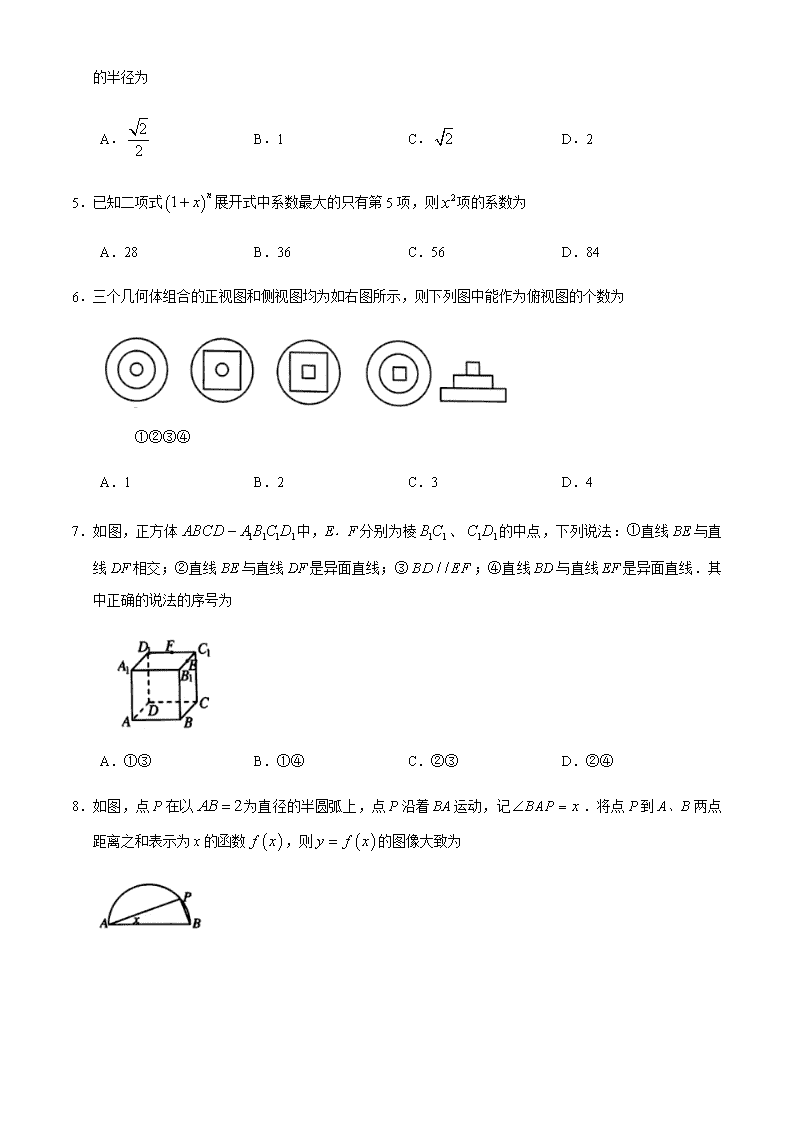
3.某班级共有50人,把某次数学测试成绩制作成直方图如图,若分数在内为优秀,则任取两人成绩均为优秀的率为
A. B. C. D.
4.已知椭圆的焦点为F,短轴端点为P,若直线PF与圆相切,则圆O
的半径为
A. B.1 C. D.2
5.已知二项式展开式中系数最大的只有第5项,则项的系数为
A.28 B.36 C.56 D.84
6.三个几何体组合的正视图和侧视图均为如右图所示,则下列图中能作为俯视图的个数为
①②③④
A.1 B.2 C.3 D.4
7.如图,正方体中,E.F分别为棱、的中点,下列说法:①直线BE与直线DF相交;②直线BE与直线DF是异面直线;③;④直线BD与直线EF是异面直线.其中正确的说法的序号为
A.①③ B.①④ C.②③ D.②④
8.如图,点P在以为直径的半圆弧上,点P沿着BA运动,记.将点P到A、B两点距离之和表示为x的函数,则的图像大致为
A. B. C D.
9.在直角中,,,,,,设BF与CE交于G,则
A. B. C. D.
10.设函数是奇函的导函数,,当时,.已知,,,则
A. B. C. D.
11.已知F为双曲线的右焦点,点P在C上,且轴,M为OP的中点(O为坐标原点),且,则双曲线C的离心率为
A. B. C. D.
12.已知中,BC边上的中线,,,则的周长为
A. B. C. D.
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分.
13.已知,则____________.
14.函数在)处的切线在y轴上的截距为____________.
15.已知a与的等差中项为,等比中项为,则____________.
16.已知A,B,C是球O的球面上三点,,,,D为该球面上的动点,若三棱锥D-ABC体积的最大值为,则球O的表面积为____________.
三、解答题:共70分,解答应写出文字说明,证明过程或演算步骤.
(一)必考题(共60分)
17.(本小题满分12分)
已知等差数列中,,,等比数列的各项均为正数,且,.
(1)求数列,的通项公式;
(2)若n,求数列的前n项和.
18.(本小题满分12分)
如图,直三棱柱中,底面为等腰直角三角形,,,P是侧棱上的点.
(1)若,证明:P是的中点;
(2)若,求二面角B-AP-C的余弦值.
19.(本小题满分12分)
2020年上半年,随着新冠肺炎疫情在全球蔓延,全球超过60个国家或地区宣布进入紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为2020年第一季度企业成立年限与倒闭分布情况统计表
企业成立年份
2019
2018
2017
2016
2015
企业成立年限
1
2
3
4
5
倒闭企业数量(万家)
5.23
4.70
3.72
3.12
2.42
倒闭企业所占比例
根据上表,给出两种回归模型:
模型①:建立曲线性回归模型,求得回归方程为;
模型②:建立线性回归模型.
(1)根据所给的统计量,求模型②中y关于x的回归方程;
(2)根据下列表格中的数据,比较两种模型的相关指数,并选择拟合精度更高、更可靠的模型,预测2014年成立的企业中倒闭企业所占比例(结果保留整数).
回归模型
模型①
模型②
回归方程
5.80
0.66
参考公式:,,.
参考数据:,,,,,.
20.(本小题满分12分)
设函数.
(1)讨论的单调性;
(2)若存在极值,对于任意,都有恒成立,求的取值范围.
21.(本小题满分12分)
已知抛物线与直线相交于A,B两点,线段AB的长为8.
(1)求抛物线C的方程;
(2)过点的直线l与抛物线C交于M.N两点,点P为直线上的任意一点,设直线PM,PQ,PN的斜率分别为,且满足,能否为定值?若为定值,求出的值;若不为定值,请说明理由.
(二)选考题(共10分.请考生在第22.23题中任选一题作答.如果多做,则按所做的第一计分.)
22.(本小题满分10分)选修4-4(坐标系与参数方程)
在直角坐标系xOy中,曲线(t为参数),其中,在以O为极点x轴正半轴为极轴的极坐标系中,曲线.
(1)求的直角坐标方程;
(2)当时,设与相交于A,B两点,求的值.
23.(本小题满分10分)选修4-5(不等式选讲):
已知,,,函数.
(1)当,时,求不等式的解集;
(2)当的最小值为5时,证明:.
2020届高中毕业班第四次模拟考试
理科数学答案提示
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.由得,∴,选(D)
2.由在复平面上位于第四象限知,
由得,∴,选(C)
3.由直方图知优秀人数为,
所以任取两人成绩均为优秀的概率为,选(B)
4.取,则PF的方程为,
∴,选(B)
5.二项式展开式中系数最大的项为中间项,所以二项式展开式中共有9项,
∴,,所以项的系数为28,选(A)
6.由正视图和侧视图知三个几何体可以是圆柱或底面为正方形的直棱柱,
所以四个图都可能作为俯视图,选(D)
7.∵,,∴,即③正确;
由③知BE与DF共面,所以直线BE与直线DF相交,即①正确,选(A)
8.,图象(D)符合,选(D)
9.如图,以A坐标原点建立坐标系,
则,,∴,,
所以直线CE的方程为,直线BF的方程为,
解,得
∴,,
∴,选(B)
10.∵,
∴在上是增函数,
又,所以,
所以当时,,当时,,
∴
∵,
∴,选(A)
11.如图,设双曲线的左焦点为,
则,,∴
∴,
∴,选(C)
12.,
,
∴,
又,
∴,
∴,
所以的周长为,选(A)
二、填空题:本大题共4小题,每小题5分,共20分.请把答案填写在题中的横线上.
13..
14.,所以在处的切线方程为,
令得,即在y轴上的截距为2.
15.依题意得,,
所以,为方程的两根,
∴,或,,
∴或,
应填:31或17.
16.如图,
由得,
所以的外接圆的圆心在AB的中点G上,
所以平面ABC,
当D、O、G三点共线时,三棱锥D-ABC体积的最大,
由得,
设球的半径为R,则,即,
所以球O的表面积为.
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17.解:(1)设公差为d,公比为q,
则由得,
∴,
由得或(舍去),
∴;
(2)
∴.
18.解:(1)由直三棱柱得平面ABC,
∴,,∴,
又,∴,
又,∴,
,即P是的中点;
(2)如图,以C为坐标原点建立空间直角坐标系,
设,则,,,
∴,,
设平面BAP的法向量为,
则由得
令得,,
∴,
又平面CAP的法向量为,
∴.
所以二面角的余弦值为.
19.解:(1)由,,可得,
所以,
则,
所以模型②中y关于x的回归方程为.
(2)因为,
所以模型①的小于模型②,说明回归方程②刻画的拟合效果更好,
选择模型②,当时,,
所以预测2014年成立的企业中倒闭企业所占比例为.
20.解:(1),,
①当时,,
即,所以在上是增函数;
②当时,令,
则,
∴,,
所以时,,
时,,
所以在上是减函数,
在上是增函数;
(2)由存在极值知,
“对于任意,都有恒成立”等价于
“对于任意,都有恒成立”,
设,,
则,,
设,,
则,,
所以在上是减函数,
又,所以时,
,时,,
所以在上是增函数,在上是减函数,
,
∴,∴.
21.解:(1)把代入得
,
∴,,
∴
,
∴,所以抛物线C的方程为;
(2)设直线l的方程为,,
,,
把代入得
,
∴,,
∴
,
∴
∴,所以为定值2.
22.解:(1)由得,
把,代入得
,
即的直角坐标方程;
(2)当时,曲线,(为参数),
代入,
∴,,
∴.
23.解:(1)不等式可化为,
当时,,∴;
当时,,∴无解;
当时,,∴.
不等式的解集为.
(2)∵
,
∴
.