北京课改版数学七下《类比》同步练习 4页

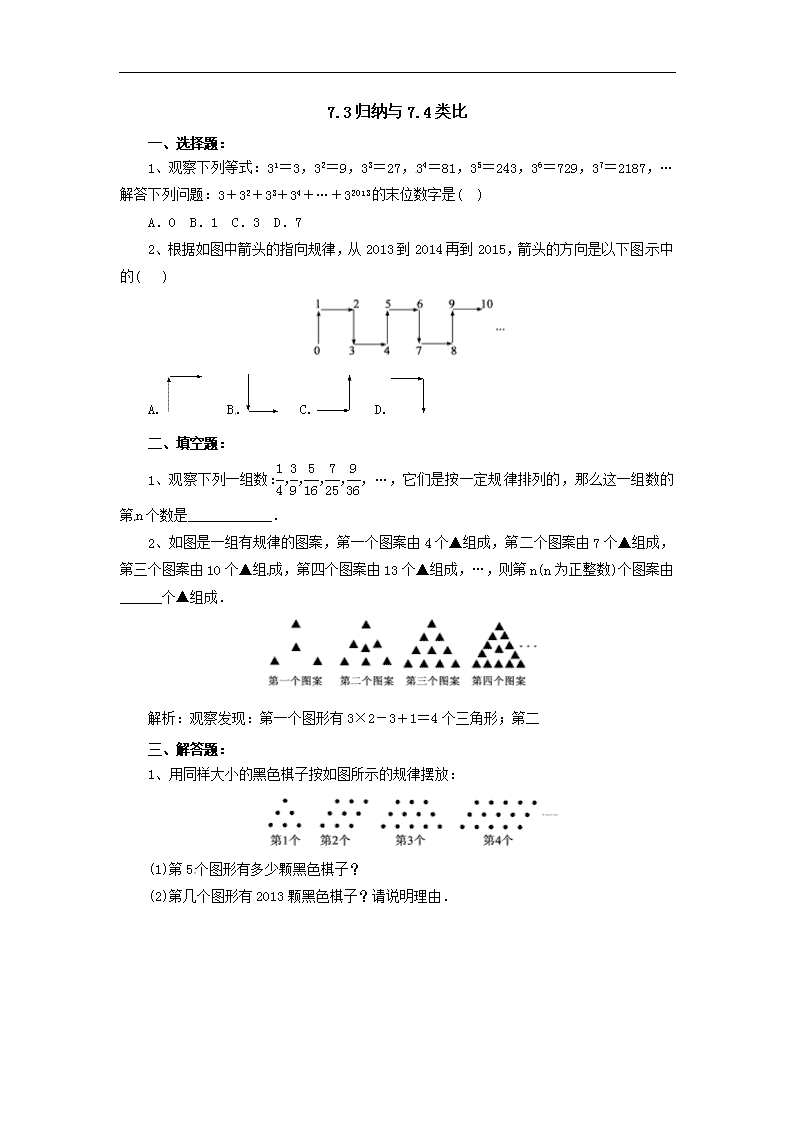
7.3 归纳与 7.4 类比 一、选择题： 1、观察下列等式：31＝3，32＝9，33＝27，34＝81，35＝243，36＝729，37＝2187，…解 答下列问题：3＋32＋33＋34＋…＋32013 的末位数字是( ) A．0 B．1 C．3 D．7] 2、根据如图中箭头的指向规律，从 2013 到 2014 再到 2015，箭头的方向是以下图示中 的( ) A. B. C. D. 二、填空题： 1、观察下列一组数：1 4 ，3 9 ，5 16 ，7 25 ，9 36 ，…，它们是按一定规 律排列的，那么这一组数的 第n 个数是____________． 2、如图是一组有规律的图案，第一个图案由 4 个▲组成，第二个图案由 7 个▲组成， 第三个图案由 10 个▲组 成，第四个图案由 13 个▲组成，…，则第 n(n 为正整数)个图案由 ______个▲组成． 解析：观察发现：第一个图形有 3×2－3＋1＝4 个三角形；第二 三、解答题： 1、用同样大小的黑色棋子按如图所示的规律摆放： (1)第 5 个图形有多少颗黑色棋子？ (2)第几个图形有 2013 颗黑色棋子？请说明理由． 2、如图，由等圆组成的一组图中，第 1 个图由 1 个圆组成，第 2 个图由 7 个圆组成， 第 3 个图由 19 个圆组成，…，按照这样的规律排列下去，则第 9 个图形由多少个个圆组成？ 参考答案 一、选择题： 1、C 2、D 二、填空题： 1、 2n－1 （n＋1）2 2、3n＋1[ 三、解答题： １、解：(1)第一个图需棋子 6＝3×2，第二个图需棋子 9＝3×3，第三个图需棋子 12 ＝3×4，第四个图需棋子 15＝3×5，∴第五个图需棋子 3×6＝18.答：第 5 个图形有 18 颗 黑色棋子. (2)由(1)可得，第 n 个图需棋子 3(n＋1)颗，设第 n 个图形有 2013 颗黑色棋子， 则 3(n＋1)＝2013，解得 n＝670.答：第 670 个图形有 2013 颗黑色棋子. 2、解：观察分析可得：第 1 个图有 1 个圆； 第 2 个图由 7 个圆组成，7＝1＋6； 第 3 个图由 19 个圆组成，19＝1＋6＋2×6；…… 故第 9 个图由 1＋6＋2×6＋3×6＋…＋8×6＝1＋(1＋2＋3＋…＋8)×6＝217(个)圆组 成．