【数学】内蒙古呼和浩特市2020届高三第二次质量普查调研考试（二模）试题（理）（解析版） 17页

内蒙古呼和浩特市2020届高三第二次质量普查调研考试 ‎（二模）数学试题（理）‎ 第Ⅰ卷 一、单项选择题（本题共12小题，每小题5分，共60分.在每小题给出的四个选项中只有一项是符合题目要求的）‎ ‎1.若复数z满足，则z的虚部为（ ）‎ A. 1 B. ‎2 ‎C. D. ‎ ‎【答案】A ‎【解析】，故，故虚部为.‎ 故选：A.‎ ‎2.设，集合，则（　　）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】由 得： ，所以 ，因此 ，故答案为B ‎3.已知为第三象限角，且，，则m的值为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】，则，‎ 解得，为第三象限角，则，故.‎ 故选：C.‎ ‎4.已知，且，，则（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】根据条件，∴.‎ 故选：A.‎ ‎5.每到春夏交替时节，雌性杨树会以满天飞絮的方式来传播下一代，漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等，给人们造成困扰，为了解市民对治理杨絮方法的赞同情况，某课题小组随机调査了部分市民（问卷调査表如下表所示），并根据调查结果绘制了尚不完整的统计图表（如下图）‎ 由两个统计图表可以求得，选择D选项的人数和扇形统计图中E的圆心角度数分别为（ ）‎ A. 500，28.8° B. 250，28.6° C. 500，28.6° D. 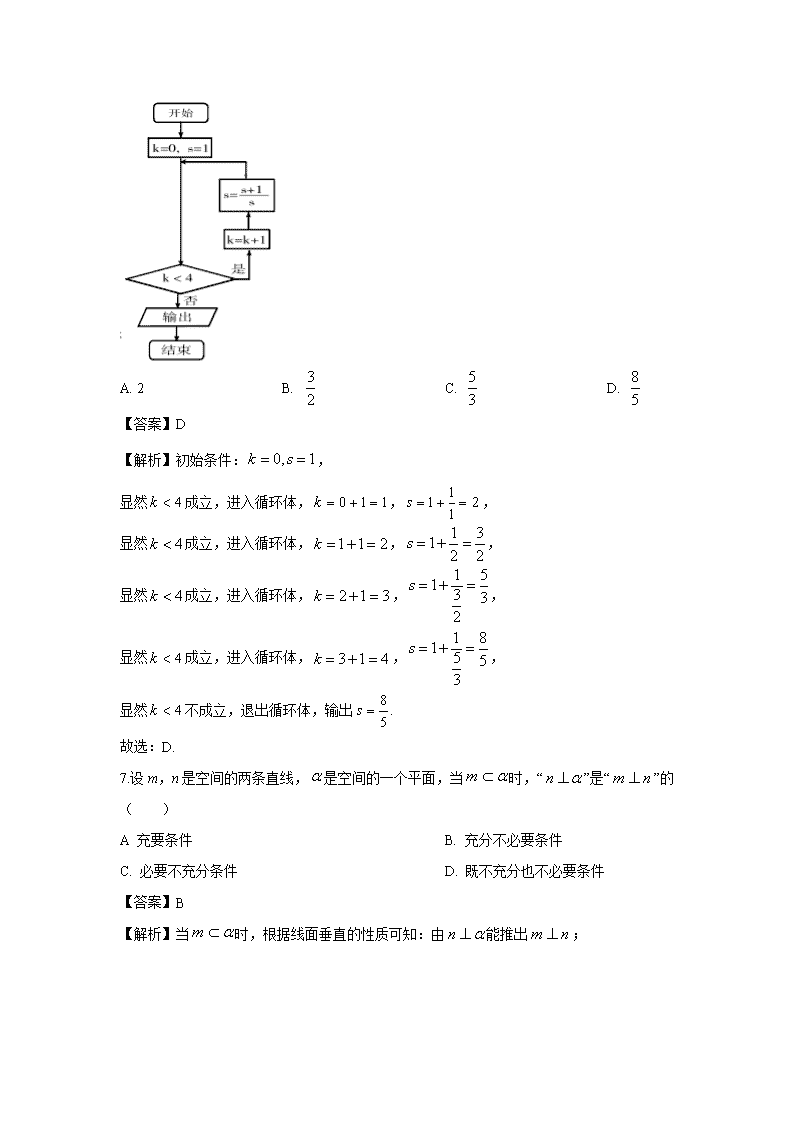250，28.8°‎ ‎【答案】A ‎【解析】设接受调查市民的总人数为，由调查结果条形图可知选择A的人数为300，通过调查结果扇形统计图可知：选择A的人数的比例为，因此有，‎ 而选择D选项的人数为：，‎ 扇形统计图中E的圆心角度数为：‎ ‎.‎ 故选：A.‎ ‎6.执行如图所示的程序框图，输出的s值为（ ）‎ A. 2 B. C. D. ‎ ‎【答案】D ‎【解析】初始条件：，‎ 显然成立，进入循环体，，，‎ 显然成立，进入循环体，，，‎ 显然成立，进入循环体，，，‎ 显然成立，进入循环体，，，‎ 显然不成立，退出循环体，输出.‎ 故选：D.‎ ‎7.设m，n是空间的两条直线，是空间的一个平面，当时，“”是“”的（ ）‎ A 充要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分也不必要条件 ‎【答案】B ‎【解析】当时，根据线面垂直的性质可知：由能推出；‎ 当时，根据线面垂直的定义可知；只有当直线与平面内所有的直线都垂直时，才有，所以仅有是推不出成立的，因此当时，“”是“”的充分不必要条件.‎ 故选：B.‎ ‎8.函数的图象向右平移个长度单位后，得到的图象对应的函数解析式为，则下面四个判断：①在上单调递增；②在上单调递增；③；④是的一个对称中心.其中正确的判断有（ ）‎ A. 4个 B. 3个 C. 2个 D. 1个 ‎【答案】D ‎【解析】，‎ 当时，，函数在端点处无意义，①错误；‎ 当时，，函数在处无意义，②错误；‎ ‎，③错误；‎ 当时，，故④正确.‎ 故选：D.‎ ‎9.已知实数是给定的常数，函数的图象不可能是(　 　)‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】当m=0，函数图象可能是C；‎ 当m≠0，，，‎ 设的两根为则<0，则两个极值点异号．‎ 当时，函数的图象是先减后增再减，且，‎ 函数图象可能是B；‎ 当时，函数的图象是先增后减再增，且，‎ 则函数图象可能是A，不可能是D．‎ 故选：D.‎ ‎10.已知点在椭圆的外部，则直线与圆的位置关系为（ ）‎ A. 相离 B. 相交 C. 相切 D. 相交或相切 ‎【答案】B ‎【解析】因为点在椭圆的外部，‎ 所以，即，‎ 则圆的圆心到直线的距离 ‎，‎ 所以直线与圆相交 故选：B.‎ ‎11.已知定义在R上的函数满足①，②，③在上表达式为，则函数与函数的图像在区间上的交点个数为（ ）‎ A. 5 B. ‎6 ‎C. 7 D. 8‎ ‎【答案】B ‎【解析】∵①，②，可知图像的对称中心为，图像的对称轴为，结合③画出和的部分图像，如图所示，据此可知与的图像在上有6个交点.故选B.‎ ‎12.已知分别为双曲线 的左顶点、右焦点以及右支上的动点,若恒成立，则双曲线的离心率为( )‎ A. B. C. 2 D. ‎ ‎【答案】C ‎【解析】设，又，∵，‎ ‎∴，，‎ 又，‎ ‎∴，整理得，‎ 这是P点的轨迹方程，又P点轨迹方程为，‎ ‎∴，∴，‎ 故选C.‎ 第Ⅱ卷 本卷包括必考题和选考题两部分，第13题~21题为必考题，每个试题考生都必须做答；第22题~第23题为选考题，考生根据要求做答.‎ 二、填空题（本大题共4小题，每小题5分，共20分.把正确答案填在答题卡的相应位置.）‎ ‎13. .‎ ‎【答案】‎ ‎【解析】.‎ ‎14.将标号为1，2，3的3个不同小球，随机放入5个不同的盒子A，B，C，D，E中，则恰有两个小球放入同一个盒子的概率为____________.‎ ‎【答案】‎ ‎【解析】根据题意：共有种方法；满足条件的放法有种，‎ 故.‎ 故答案为：.‎ ‎15.如图，某湿地为拓展旅游业务，现准备在湿地内建造一个观景台P，已知射线，为湿地两边夹角为120°的公路（长度均超过‎2千米），在两条公路，上分别设立游客接送点M，N，且千米，若要求观景台P与两接送点所成角与相等，记，观景台P到M，N建造的两条观光线路与之和记为y，则把y表示为的函数为y=______；当两台观光线路之和最长时，观景台P到A点的距离______千米.‎ ‎【答案】 (1). (2). 2‎ ‎【解析】，故，‎ ‎，，，‎ 在中，根据正弦定理：，‎ 故，，‎ 故，‎ 故，‎ 当时，最大，此时，为等边三角形，故.‎ 故答案为：；.‎ ‎16.已知正方体的棱长为2，平面过正方体的一个顶点，且与正方体每条棱所在直线所成的角相等，则该正方体在平面内的正投影面积是__________.‎ ‎【答案】‎ ‎【解析】正方体中所有的棱是三组平行的棱，如图所示：‎ 图中的正三角形所在的平面或者与该平面平行的平面为平面，满足与正方体每条棱所在直线所成的角相等，‎ 正三角形是平面截正方体所形成三角形截面中，截面面积最大者，正方体的棱长为2，所以正三角形的边长为：，正方体中，‎ 三个面在平面的内的正投影是三个全等的菱形，如下图所示：‎ 可以看成两个边长为的等边三角形，‎ 所以正方体在平面内的正投影面积是：‎ ‎.‎ 故答案为；‎ 三、解答题（本大题共6小题，共70分.解答应写岀文字说明，证眀过程或演算步骤.）‎ ‎17.如图，三棱柱中，D是的中点.‎ ‎（1）证明：平面；‎ ‎（2）若是边长为2的正三角形，且，，平面平面.求平面与侧面所成二面角的正弦值.‎ ‎（1）证明：连接，记，连接，故为中点，‎ D是的中点，所以，又平面，平面.‎ 故平面.‎ ‎（2）解：取边中点点O，连接，，因为，为等边三角形，，所以，，‎ 又平面平面，且平面平面，‎ 平面，所以，，两两互相垂直.‎ 故以O为原点，建立空间直角坐标系如图所示：‎ 则由题意可知，，.‎ 设平面的法向量，则，即，‎ 令，解得，得.‎ 显然平面的一个法向量为.‎ ‎∴，‎ ‎∴二面角的正弦值为.‎ ‎18.已知数列的前项和 ‎（1）求数列的通项公式；‎ ‎（2）若，求数列的前n项和.‎ 解：（1）当时，，‎ 当时，，①‎ 所以有，②‎ ‎①②得：，‎ 经检验不符合上式，‎ ‎∴；‎ ‎（2）由（1）得当时，，‎ 当时 ‎∴ ‎ ‎∴‎ ‎.‎ ‎.‎ ‎19.已知一条曲线C在y轴右侧，曲线C上任意一点到点的距离减去它到y轴的距离都等于1.‎ ‎（1）求曲线C的方程；‎ ‎（2）直线与轨迹C交于A，B两点，问：在x轴上是否存在定点，使得直线与关于x轴对称而与直线的位置无关，若存在，求出点M的坐标，若不存在，请说明理由.‎ 解：（1）设是曲线C上任意一点，那么点满足：，‎ 化简得，又因曲线C在y轴右侧，故，‎ 所以曲线C方程为：. ‎ ‎（2）在x轴上存在定点使得直线与关于x轴对称而与位置无关.‎ 理由如下：‎ 设直线与曲线C的交点坐标为，， ‎ 由，消去x，整理得，，‎ 由韦达定理得，，. ‎ 假设存在点，使得直线与关于x轴对称而与位置无关，‎ 则对任意实数m恒成立，即对任意实数m恒成立，‎ 而，所以，‎ 所以，又，所以.‎ 故当对任意实数m，，‎ 即在x轴上存在点，使得直线与关于x轴对称而与位置无关.‎ ‎20.为了更好地贯彻党的“五育并举”的教育方针，某市要对全市中小学生“体能达标”情况进行了解，决定通过随机抽样选择几个样本校对学生进行体能达标测试，并规定测试成绩低于60分为不合格，否则为合格，若样本校学生不合格人数不超过其总人数的5%，则该样本校体能达标为合格.已知某样本校共有1000名学生，现从中随机抽取40名学生参加体能达标测试，首先将这40名学生随机分为甲、乙两组，其中甲乙两组学生人数的比为3:2，测试后，两组各自的成绩统计如下：甲组的平均成绩为70，方差为16，乙组的平均成绩为80，方差为36.‎ ‎（1）估计该样本校学生体能测试的平均成绩；‎ ‎（2）求该样本校40名学生测试成绩的标准差s；‎ ‎（3）假设该样本校体能达标测试成绩服从正态分布，用样本平均数作为的估计值，用样本标准差s作为的估计值，利用估计值估计该样本校学生体能达标测试是否合格？‎ ‎（注：1.本题所有数据的最后结果都精确到整数；2若随机变量z服从正态分布，则，，）‎ 解：（1）由题知，甲、乙两组学生数分别为24和16，‎ 则这40名学生测试成绩的平均分 ‎ 故可估计该样本校学生体能测试的平均成绩为74，. ‎ ‎（2）由变形得 设第一组学生的测试成绩分别为，‎ 第二组学生的测试成绩分别为，‎ 则第一组的方差为 ‎，‎ 解得.‎ 第二组的方差为 解得.‎ 这40名学生的方差为 ‎，‎ 所以.‎ 综上，标准差.‎ ‎（3）由，，得的估计值为，的估计值 由，‎ 得，‎ 即 所以. ‎ 从而，在全校1000名学生中，“不合格”的有（人） ‎ 而，‎ 故可估计该样本校学生“体能达标”测试合格.‎ ‎21.已知函数.‎ ‎（1）若函数的极小值为1，求实数m的值；‎ ‎（2）若函数在时，其图象全部都在第一象限，求实数m的取值范围.‎ 解：（1），，‎ ‎①若，则在R上恒成立，‎ ‎∴在单调递增，所以无极值；‎ ‎②若，当时，，当时，，‎ 即在单调递减，在单调递增，‎ 所以的极小值为，由，解得.‎ 综上所述：.‎ ‎（2），函数图像全部在第一象限，等价于时，恒成立，‎ 令，，‎ 令，，令，‎ 显然在单调递增，∴. ‎ 当时，，所以，∴在单调递增，‎ ‎∴，即，∴在单调递增，‎ 所以，此时符合题意； ‎ 当时，，∴，使，‎ 故在恒为负值，在单调递减，此时，‎ 所以在单调递减，所以，此时不符合题意. ‎ 故所求m的取值范围为.‎ 请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题记分.做答时用2B铅笔在答题卡上把所选题目对应的题号涂黑 ‎【选修4-4坐标系与参数方程】‎ ‎22.在极坐标系中，已知极点为O，点A的极坐标为，动点P满足.‎ ‎（1）写出动点P的轨迹C的极坐标方程；‎ ‎（2）已知直线和与轨迹C分别交于异于极点O的点，并分别记为M、N，点D是线段的中点，求出与的面积.‎ 解：（1）设，因为，所以，.‎ 因此三角形是直角三角形，在中，‎ 有，或 ‎∴，或，而，‎ 故所求极坐标方程为；‎ ‎（2）将和分别代入得 ‎，，‎ 显然，，‎ 故 ‎ 又是线段的中点，故 ‎【选修4-5不等式选讲】‎ ‎23.（1）已知，，比较A与B的大小；‎ ‎（2）已知，求证：，，中至少有一个不大于.‎ ‎（1）解：因为 所以，当且仅当，时等号成立. ‎ ‎（2）证明：假设，，三个均大于. ‎ 因为，所以，，，‎ 根据基本不等式得：‎ ‎，‎ ‎，‎ ‎，‎ 所以，出现矛盾. ‎ 所以假设不成立，即，，中至少有一个不大于.‎