- 4.48 MB
- 2021-05-07 发布
湖南省湘东七校2019年下期高三联考
文科数学试题
总分:150分 时量:120分钟 考试时间:2019年12月8日
由株洲二中·浏阳一中·攸县一中·株洲八中·株洲四中·九方中学·醴陵一中联合命题
姓名 考号
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、集合,,则( )
A. B. C. D.
2、复数满足,则( )
A. 2 B. C.1 D.
3、已知条件,条件,则是成立的( )
A. 充分不必要条件 B.必要不充分条件 C.充要条件 D.既非充分也非必要条件
4、《莱茵德纸草书》是世界上最古老的数学著作之一,书中有一道这样的题目:把120个面包分给5个人,使每个人所得份量成等差数列,且较大的三份之和的七分之一是较小的两份之和,则最大一份的个数为( )
A.2 B.15 C.32 D.46
5、函数()在处取得最大值,则( )
A.是偶函数 B.是奇函数 C.是偶函数 D.是奇函数
6、已知曲线在处的切线与直线垂直,则实数的值为( )
A. 2 B. C. D.
7、在中,,点满足,则( )
A. B. C. 4 D.8
8、已知在处取得极值,则的最小值为( )
A. B. C. D.
9、,则( )
A. B. C. D.
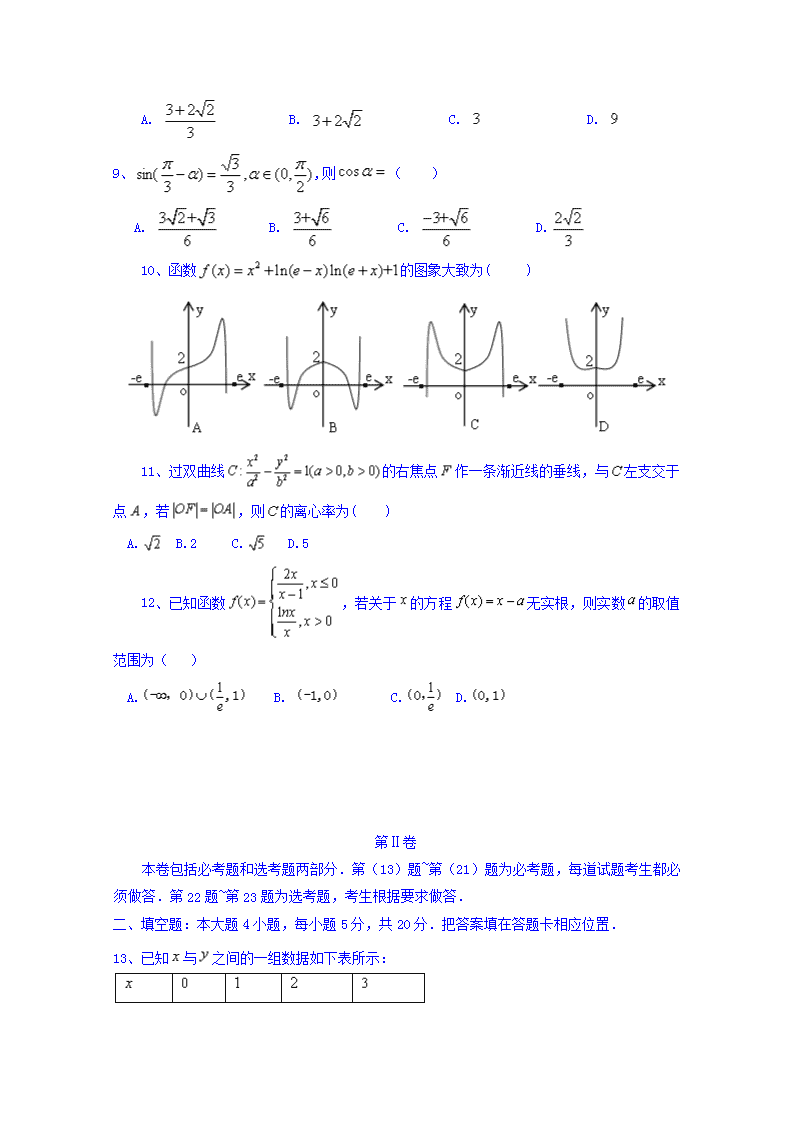
10、函数的图象大致为( )
11、过双曲线的右焦点作一条渐近线的垂线,与左支交于点,若,则的离心率为( )
A. B.2 C. D.5
12、已知函数,若关于的方程无实根,则实数的取值范围为( )
A. B. C. D.
第Ⅱ卷
本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每道试题考生都必须做答.第22题~第23题为选考题,考生根据要求做答.
二、填空题:本大题4小题,每小题5分,共20分.把答案填在答题卡相应位置.
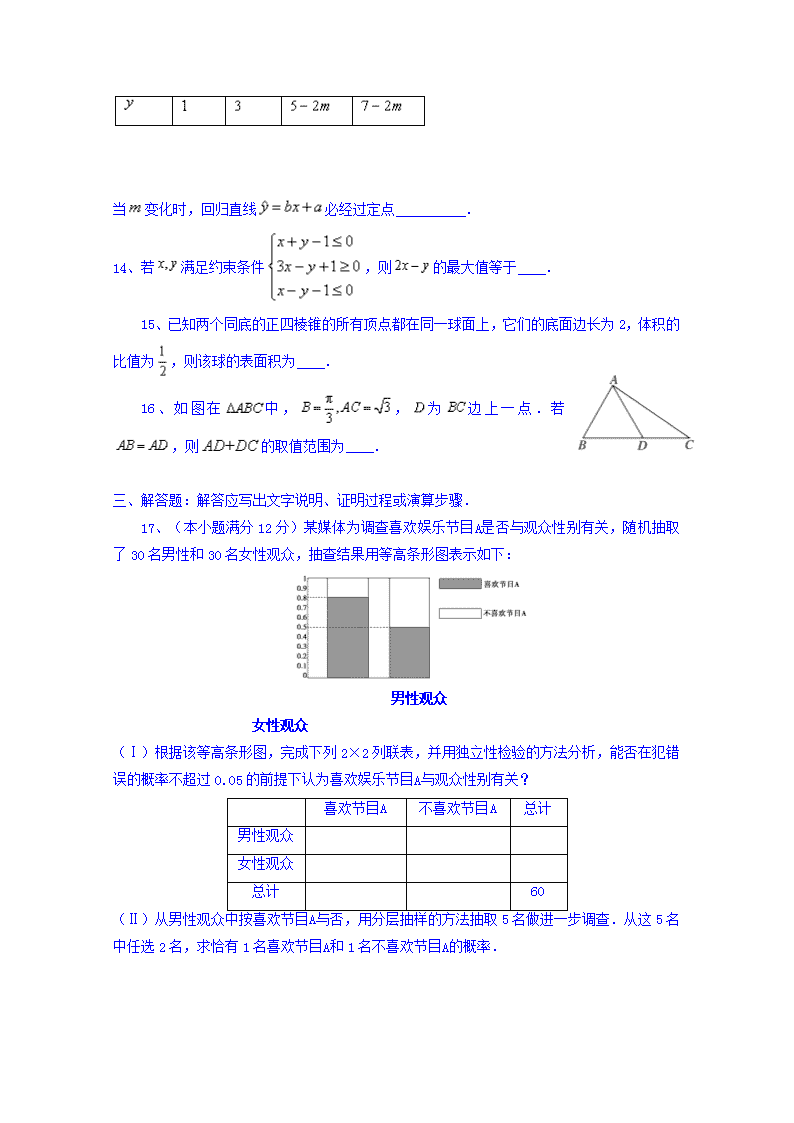
13、已知与之间的一组数据如下表所示:
当变化时,回归直线必经过定点 .
14、若满足约束条件,则的最大值等于 .
15、已知两个同底的正四棱锥的所有顶点都在同一球面上,它们的底面边长为2,体积的比值为,则该球的表面积为 .
16、如图在中,,为边上一点.若,则的取值范围为 .
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17、(本小题满分12分)某媒体为调查喜欢娱乐节目A是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如下:
男性观众 女性观众
(Ⅰ)根据该等高条形图,完成下列2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关?
喜欢节目A
不喜欢节目A
总计
男性观众
女性观众
总计
60
(Ⅱ)从男性观众中按喜欢节目A与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目A和1名不喜欢节目A的概率.
18、(本小题满分12分)如图所示,四棱锥的底面是梯形,且平面,是中点,.
(Ⅰ)求证:;
(Ⅱ)若,求三棱锥的高.
19、(本小题满分12分)已知数列的前项和为,.
(Ⅰ)求证:数列是等差数列;
(Ⅱ)若,设数列的前n项和为Tn,求T2n.
20、(本小题满分12分)在平面直角坐标系中,已知椭圆的左顶点为,右焦点为,为椭圆上两点,圆.
(Ⅰ)若轴,且满足直线与圆相切,求圆的方程;
(Ⅱ)若圆的半径为2,点满足,求直线被圆截得弦长的最大值.
21、(本小题满分12分)已知函数,.
(Ⅰ)讨论函数的单调性;
(Ⅱ)当时,≤恒成立,求的取值范围.
请考生在第22、23两题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清题号.
22、(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线的参数方程为(为参数).以为极点,轴的正半轴为极轴建立极坐标系.
(Ⅰ)写出的极坐标方程;
(Ⅱ)设曲线经伸缩变换后得到曲线,曲线()分别与和交于,两点,求.
23、
(本小题满分10分)选修4-5:不等式选讲
已知不等式的解集为.
(Ⅰ)求的值;
(Ⅱ)设关于的方程()有实数根,求实数的值.
湖南省湘东七校2019年下期高三联考
文科数学试题答案及评分参考
一、选择题:本大题考查基础知识和基本运算.每小题5分,满分60分.
1、C 2、B 3、C 4、D 5、A 6、B
7、D 8、C 9、B 10、C 11、C 12、D
12.解析:因为函数,所以方程无实根等价于函数的图像与直线无交点.由图像知,若,则直线与曲线必有交点,则.设直线与曲线相切时,切点为,由,得解得,则,所以切线方程为得.由图像知实数的取值范围为,选D
二、填空题:本大题考查基础知识和基本运算.每小题5分,满分20分.
13、 14、2 15、 16、
15.解析:易知球心在两四棱锥顶点连线的中点,设体积较小的锥体的高为,则
解得,半径为,所以表面积为
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17、本小题主要考查等高条形图、独立性检验、古典概型等基础知识,考查数据处理能力、运算求解能力以及应用意识,考查必然与或然思想等.满分12分.
解:(Ⅰ)由题意得列联表如下:
喜欢节目A
不喜欢节目A
总计
男性观众
24
6
30
女性观众
15
15
30
总计
39
21
60
3分
假设喜欢娱乐节目A与观众性别无关,
则的观测值, 5分
所以能在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目A与观众性别有关.
6分
(Ⅱ)利用分层抽样在男性观众30名中抽取5名,其中喜欢娱乐节目A的人数为,
不喜欢节目A的人数为. 7分
被抽取的喜欢娱乐节目A的4名分别记为;不喜欢节目A的1名记为.
则从5名中任选2人的所有可能的结果为:,共有10种. 9分
其中恰有1名喜欢节目A和1名不喜欢节目A的有,共4种.…… 10分
所以所抽取的观众中恰有1名喜欢节目A和1名不喜欢节目A的观众的概率是:.…… 12分
18、本小题主要考查空间直线与直线、直线与平面的位置关系及三棱锥的高等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查化归与转化思想等.满分12分.
(Ⅰ)证明:取的中点,连结,如图所示.
因为点是中点,
所以且. 1分
又因为且,
所以且, 2分
所以四边形为平行四边形,
所以, 3分
因为平面,平面,
所以. 4分
所以. 5分
(Ⅱ)解:设点为的中点,连结,如图所示,
因为,
由(Ⅰ)知, 6分
又因为,所以,
所以 7分
所以为正三角形, 8分
所以,且. 9分
因为平面,,
所以平面. 10分
因为平面,
所以, 11分
又因为,所以平面.
所以三棱锥的高为. 12分
19、本小题主要考查与的关系、等差数列的定义与通项公式、数列求和等基础知识,考查运算求解能力,考查化归与转化思想等.满分12分.
解:(Ⅰ)证明:因为当时,,
所以. 1分
所以, 2分
因为所以,所以, 3分
所以. 4分
所以是以为首项,以1为公差的等差数列. 6分
(Ⅱ)由(Ⅰ)可得,所以. 8分
9分
∴
12分
20、解:(Ⅰ)因为椭圆的方程为,所以,. ...............1分
因为轴,所以,而直线与圆相切,
根据对称性,可取, ...............2分
则直线的方程为,即. ......3分
由圆与直线相切,得,所以圆的方程为. ...............5分
(Ⅱ)易知,圆的方程为.
①当轴时,,所以,
此时得直线被圆截得的弦长为. ...............7分
②当与轴不垂直时,设直线的方程为,
,
首先由,得,
即,所以(*). ..........9分
联立,消去,得,在时
代入(*)式,得. ……………10分
由于圆心到直线的距离为,
所以直线被圆截得的弦长为,故当时,有最大值为.
综上,因为,所以直线被圆截得的弦长的最大值为. ……………12分
21、解:(Ⅰ)的定义域为, ...............1分
若则在上单调递增, ...............2分
若则由得,当时,当时,,
在上单调递增,在单调递减.
综上:当时,在上单调递增,
当时, 在上单调递增,在单调递减. ...............5分
(Ⅱ),
令,
,令,...............7分
. ..............8分
(2),
以下论证同(1)一样,所以不符合题意 ................10分
,
,
,
综上所述,的取值范围是 ...............12分
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.
22、选修;坐标系与参数方程
本小题考查极坐标方程和参数方程、伸缩变换等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想等.满分10分.
解:(Ⅰ)将消去参数,化为普通方程为,
即, 2分
将代入,得, 4分
所以的极坐标方程为. 5分
(Ⅱ)将代入得,
所以的方程为. 7分
的极坐标方程为,所以.
又,所以. 10分
23、选修:不等式选讲
本小题考查绝对值不等式的解法与性质、不等式的证明等基础知识,考查运算求解能力、推理论证能力,考查分类与整合思想、化归与转化思想等. 满分10分.
解:(Ⅰ)由得,
或 2分
解得.依题意. 5分
(Ⅱ)因为
当且仅当时取等号, 7分
因为关于的方程()有实数根,
所以. 8分
另一方面,,所以, 9分
所以或. 10分