浙江省效实中学2019-2020学年高二上学期期中考试数学（3-8班）试题 4页

数学(高二)第 1 页 共 4 页 宁波效实中学 二○一九学年度 第 一 学期 期中考试高二数学试卷 请将所有题目的答案填写在答卷的相应位置 参考公式： 柱体的体积公式：V Sh （其中 S 表示柱体的底面积， h 表示柱体的高） 锥体的体积公式： 1 3V Sh （其中 表示锥体的底面积，表示 锥体的高） 球的表面积公式： 2=4SR （其中 表示球的半径） 球的体积公式 ： 34 3VR （其中 表示球的半径） 台体的体积公式： 1 1 2 2 1()3V S S S S h   （其中 1S ， 2S 分别表示台体的上、下底面积， 表示台体的高 ） 第Ⅰ卷（选择题 共 30 分） 一、选择题：本大题共 10 小题，每小题 3 分，共 30 分．在每小题给出的四个选项中只有 一项是符合题目要求的． 1.空间中，已知 ,ab是直线， ,是平面，且 , , / /ab    ，则 的位置关系是 A． 平行 B． 相交 C．异面 D．平行或异面 2.已知椭圆 22 13 xy m 的焦点在 x 轴上，离心率为 2 2 ，则 m 的值是 A．32 B． 32 2 C． 6 D．6 3.椭圆过点(2，0)，长半轴长是焦距的 2 倍，则椭圆的标准方程为 A． 224 14 15 xy B． 22 143 xy C． 2 2 2 244114 15 15 4 或x y x y    D． 2 2 2 24 15114 15 4 64 或x y x y    4. 在长方体 1 1 1 1ABCD ABC D 中， 2AB  ， 1 1BC AA， ,EF分别为 1 1 1 1,A B C D 的中 点，则异面直线 AF 与 BE 所成角的余弦值为 A．0 B． 5 5 C． 3 2 D． 5 5 5．设 ,,   是三个不同的平面， ,,m n l 是三条不同的直线，则下列命题正确的是 A．三点 ,,A B C 确定一个平面. B． m  ， n  ， mn ，则   . C． m ， n ， l ，且 m 与 n 不平行，则 ,,m n l 相交于一点. D． ， ， nm ，则 n  . h R 19、 数学(高二)第 2 页 共 4 页 1C A 1A 1B B D C 1D 第 10 题图 6.已知 A 是圆  22 1 : 2 36F x y   上的一动点，定点  2 0,2F ，线段 2FA的垂直平分线交 半径 1FA于 P 点，则 点的轨迹方程为 A． 22 195 xy B． 22 159 xy C． 22 136 32 xy D． 22 132 36 xy 7. 正三棱锥 P ABC 中， 5PA  ， 23AB  ，则该三棱锥外接球的体积为 A． 500 3  B．100 C． 25 D．125 6  8. 如图， 12,FF分别是双曲线 22 22: 1( 0 0)xyC a bab   ， 的左、右焦 点，过 1F 的直线l 与双曲线C 的两个分支分别交于点 ,AB.若 2ABF 为等边三角形，则双曲线的离心率为 A． 4 B． 23 3 C． 7 D． 3 9. 已知动直线l 过点 ( 1,0) ，且与椭圆 22 :143 xyC 交于 AB、 两点，过原点O 的直线与 椭圆C 交于 PQ、 两点，且 //PQ l ，则 2 AB PQ 的值是 A． B． 1 4 C． 23 D． 10. 长方体 1 1 1 1ABCD ABC D 中， 1 1AA  ， 6AB BC，若空 间中有一条直线l 与直线 1BB 所成角为 4  ，则直线 与平面 1D AC 所成 角的取值范围是 A． 5[ , ]6 12  B． 5[ , ]12 12  C．[ , ]42  D．[ , ]12 4  第Ⅱ卷（非选择题 共 70 分） 二、填空题：本大题共 7 小题，其中双空题每小题 4 分，单空题每小题 3 分，共 25 分． 11. 椭圆 22: 4 8C x y的长轴长为 ▲ ，焦点坐标 ▲ ． 12.已知一个圆台的上、下底面半径分别为 2cm ， 4cm ，高为3cm ，则该圆台的母线长 为 ▲ cm ；体积为 ▲ 3cm . 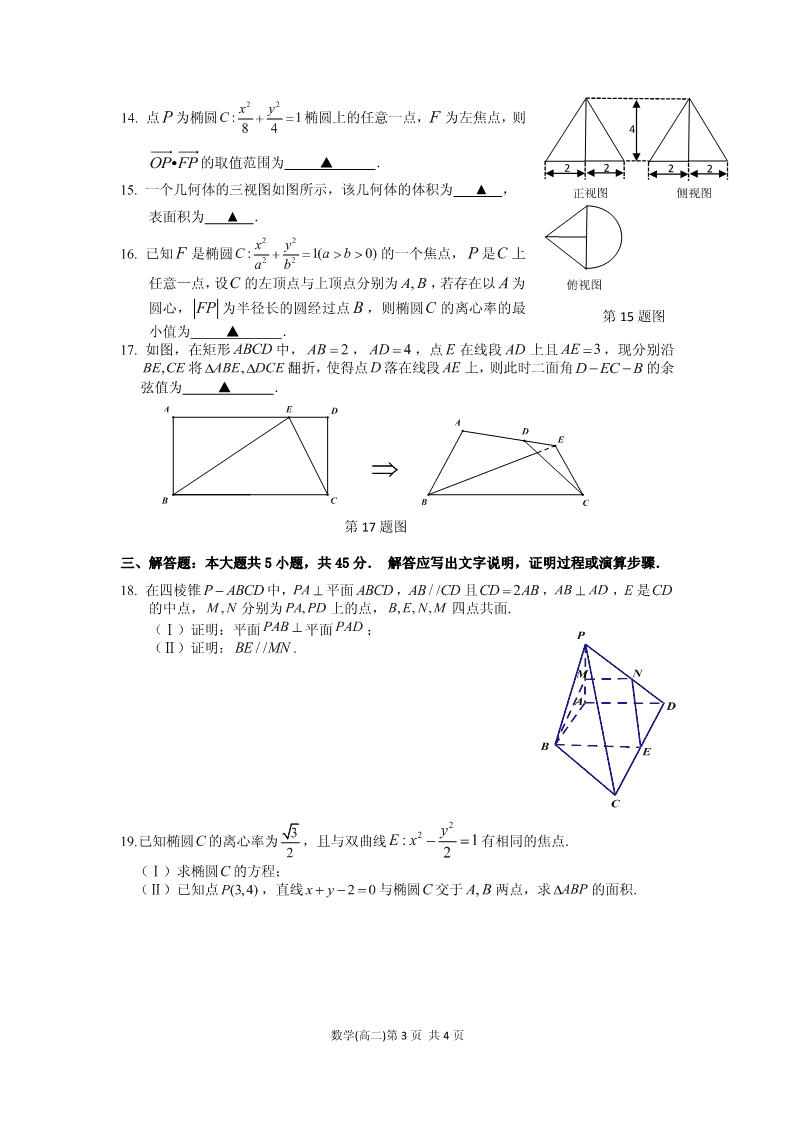13.已知过点 2,3 的双曲线C 的渐近线方程为 3yx ，则双曲线 的方程 为 ▲ ； 若点 是双曲线 上一点，且点 在第一象限内，点 12,FF为双曲 线 的焦点，且 1 2 2| | | |F F PF ，则点 的坐标为 ▲ ． 第 7 题图 数学(高二)第 3 页 共 4 页 正视图 2 2 侧视图 2 2 4 俯视图 14. 点 P 为椭圆 22 :184 xyC 椭圆上的任意一点，F 为左焦点，则 OP FP的取值范围为 ▲ ． 15. 一个几何体的三视图如图所示，该几何体的体积为 ▲ ， 表面积为 ▲ ． 16. 已知 F 是椭圆 22 22: 1( 0)xyC a bab    的一个焦点， P 是C 上 任意一点，设 的左顶点与上顶点分别为 ,AB，若存在以 A 为 圆心， FP 为半径长的圆经过点 B ，则椭圆 的离心率的最 小值为 ▲ ． 17. 如图，在矩形 ABCD 中， 2AB  ， 4AD  ，点 E 在线段 AD 上且 3AE  ，现分别沿 ,BE CE 将 ,ABE DCE翻折，使得点 D 落在线段 AE 上，则此时二面角 D EC B的余 弦值为 ▲ ． 三、解答题：本大题共 5 小题，共 45 分． 解答应写出文字说明，证明过程或演算步骤． 18. 在四棱锥 P ABCD 中，PA  平面 ABCD， //AB CD 且 2CD AB ，AB AD ，E 是CD 的中点， ,MN分别为 ,PA PD 上的点， , , ,B E N M 四点共面. （Ⅰ）证明：平面 PAB  平面 PAD ； （Ⅱ）证明： //BE MN . 19.已知椭圆C 的离心率为 3 2 ，且与双曲线 2 2:12 yEx有相同的焦点. （Ⅰ）求椭圆C 的方程； （Ⅱ）已知点 (3,4)P ，直线 20xy   与椭圆 交于 两点，求 ABP 的面积. 第 17 题图  D E C E DA B C A B A B D C P E NM 第 15 题图 数学(高二)第 4 页 共 4 页 B D C A P E M O 20.在所有棱长都为 2 的三棱柱 1 1 1ABC A B C 中， 1B BC 为正三角形， 1 3AB  . （Ⅰ）求证： 1AB BC ； （Ⅱ）求二面角 1B AB C的正切值. 21. 如 图 ， 四 边 形 ABCD 是 正方形 ， 平面 PAD  平面 ， 2AB  ， //PA BE ， PA PD BE， M 为 PD 的中点，O为 BD 的中点. （Ⅰ）求证： //BD 平面 AME ； （Ⅱ）求当 PA 是多少时， PO 与平面 PABE 所成角为30 ？ 22.已知椭圆 2 2:14 xCy （Ⅰ） M 是椭圆C 上的动点,  1,0A , 2AN MA ,求动点 N 的轨迹方程； （Ⅱ）如图，过点  0,2B 的直线 l 分别与椭圆 ，圆 224 12 0x y y    依次交于点 , , ,P N M Q ，求 PM QN 的取值范围. x y Q M B N P O C1 B1 A C B A1