- 117.55 KB
- 2021-05-06 发布
- 1 -
2.4 圆周角(1)
教学目标
【知识与能力】
了解圆周角的概念
【过程与方法】
让学生经历圆周角与圆心角关系的探索过程,培养学生的动手操作、自主探索和合作交流的
能力
【情感态度价值观】
能用圆周角与圆心角的关系进行简单的说理,培养学生合情 推理的意识,掌握说理的基本
方法,从而提高数学素养.
教学重难点
【教学重点】
探索圆周角与圆心角的关系.
【教学难点】
通过分类讨论,推理、验证“圆周角与圆心角的关系”.
课前准备
无
教学过程
情境引入
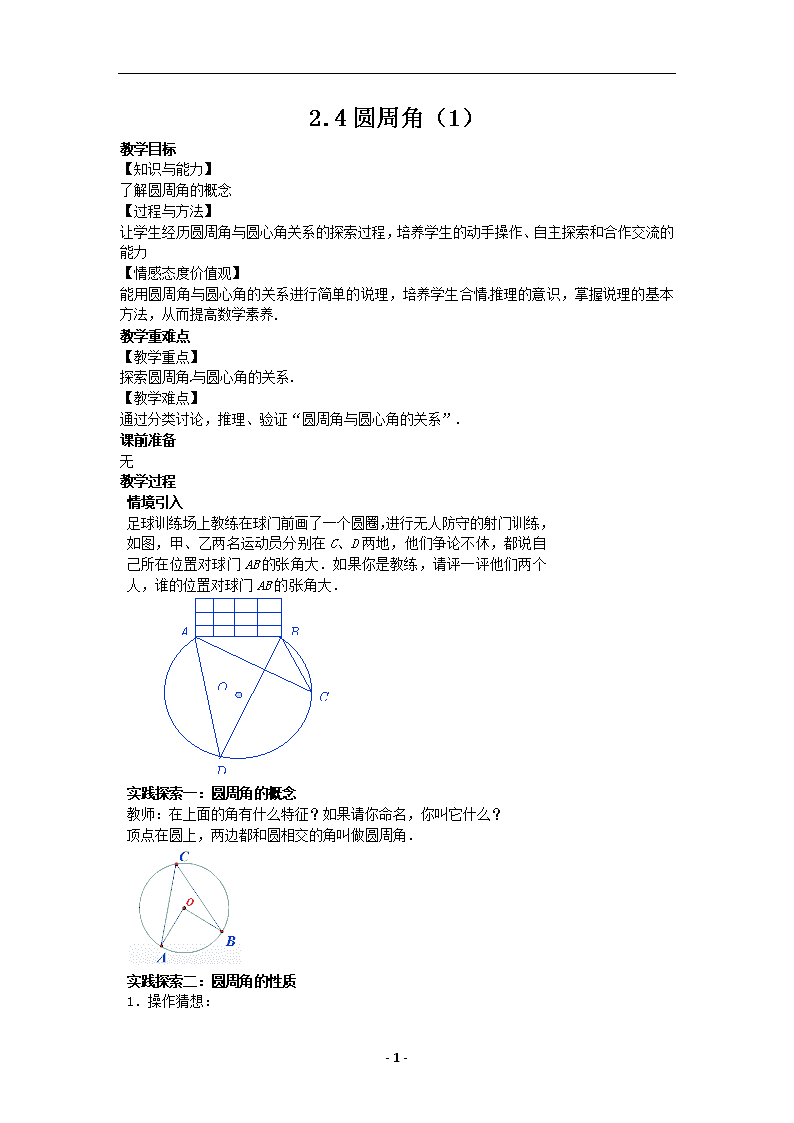
足球训练场上教练在球门前画了一个圆圈,进行无人防守的射门训
练,如图,甲、乙两名运动员分别在 C、D 两地,他们争论不休,都
说自己所在位置对球门 AB 的张角大.如果你是教练,请评一评他们
两个人,谁的位置对球门 AB 的张角大.
实践探索一:圆周角的概念
教师:在上面的角有什么特征?如果请你命名,你叫它什么?
顶点在圆上,两边都和圆相交的角叫做圆周角.
实践探索二:圆周角的性质
1.操作猜想:
A B
O C
D
- 2 -
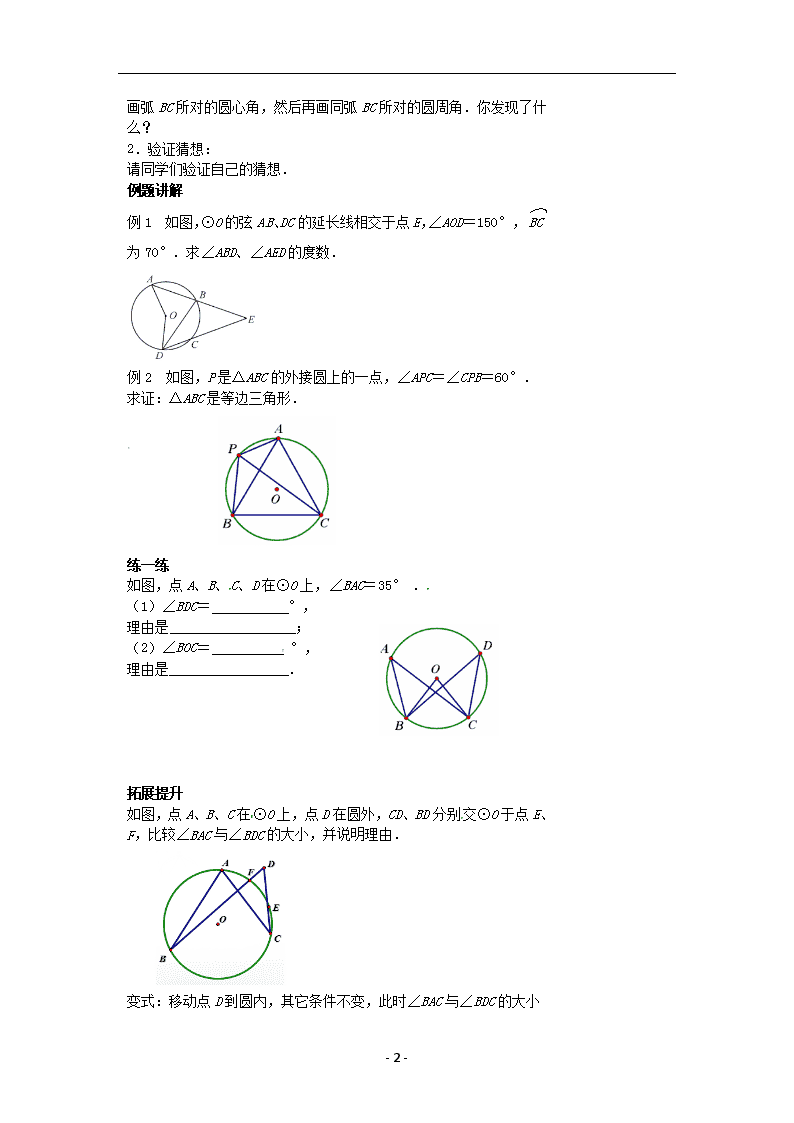
画弧 BC 所对的圆心角,然后再画同弧 BC 所对的圆周角.你发现了什
么?
2.验证猜想:
请同学们验证自己的猜想.
例题讲解
例 1 如图,⊙O 的弦 A B、DC 的延长线相交于点 E,∠AOD=150°,⌒BC
为 70°.求∠ABD、∠AED 的度数.
例 2 如图,P 是△ABC 的外接圆上的一点,∠APC=∠CPB=60°.
求证:△ABC 是等边三角形.
练一练
如图,点 A、B、C、D 在⊙O 上,∠BAC=35° .
(1)∠BDC= °,
理由是 ;
(2)∠BOC= °,
理由是 .
拓展提升
如图,点 A、B、C 在⊙O 上,点 D 在圆外,CD、BD 分别交⊙O 于点 E、
F,比较∠BAC 与∠BDC 的大小,并说明理由.
变式:移动点 D 到圆内,其它条件不变,此时∠BAC 与∠BDC 的大小
- 3 -
又如何?并说明理由.
总结
这节课你有哪些收获和困惑?开始的问题情境,你解决了吗?
相关文档
- 2017-2018学年湖北省十堰市九年级2021-05-06 13:50:508页
- 三年级数学上册课件-7长方形和正方2021-05-06 13:50:2224页
- 2018_2019学年八年级道德与法治上2021-05-06 13:50:185页
- 六年级数学下册课件-4 正比例-人2021-05-06 13:50:1720页
- 中考数学二轮精品练习:锐角三角函数2021-05-06 13:50:025页
- 沪教版 一年级数学下册三100以内2021-05-06 13:50:012页
- 山东专用2021版高考数学一轮复习考2021-05-06 13:49:537页
- 【数学】广东省韶关市2019-2020学2021-05-06 13:49:3914页
- 人教版五年级数学下册第七单元折线2021-05-06 13:49:324页
- 部编版一年级上册语文《 升国旗》2021-05-06 13:48:377页