- 250.50 KB
- 2021-05-06 发布
www.ks5u.com
课时分层作业(十一) 多面体与棱柱
(建议用时:40分钟)
一、选择题
1.下面多面体中,是棱柱的有( )
A.1个 B.2个 C.3个 D.4个
D [这4个多面体均为棱柱.]
2.设集合M={正四棱柱},N={长方体},P={直四棱柱},Q={正方体},这些集合间的关系是( )
A.Q⊇N⊇M⊇P B.Q⊇M⊇N⊇P
C.P⊇M⊇N⊇Q D.P⊇N⊇M⊇Q
D [正方体是侧棱长等于底面边长的正四棱柱,正四棱柱的上、下两个底面都是正方形,其余各面都是矩形,因此正四棱柱一定是长方体,长方体的侧棱和上、下两底面垂直,因此长方体一定是直四棱柱,故P⊇N⊇M⊇Q.]
3.已知某长方体同一顶点上的三条棱长分别为1,2,3,则该长方体的表面积为( )
A.22 B.20 C.10 D.11
A [所求长方体的表面积
S=2×(1×2)+2×(1×3)+2×(2×3)=22.]
4.如图所示的几何体,关于其结构特征,下列说法错误的是( )
A.该几何体可看作由2个同底的四棱锥组成的组合体
B.该几何体有12条棱、6个顶点
C.该几何体有8个面,并且各面均为三角形
D.该几何体有9个面,其中一个面是四边形,其余各面均为三角形
D [该几何体用平面ABCD可分割成两个四棱锥,因此它可看作两个四棱锥的组合体,但是平面ABCD是它的一个截面而不是它的一个面.故D说法不正确.]
5.正三棱柱ABCA′B′C′的底面边长是4 cm,过BC的一个平面交侧棱AA′于D,若AD的长是2 cm,则截面BCD的面积为( )
A.6 cm2 B.2 cm2 C.8 cm2 D.2 cm2
C [如图,取BC的中点E,连接AE,DE,
则AE⊥BC,DE⊥BC.
因为AE=×4=2,
所以DE==4,
所以S△BCD=BC·ED
=×4×4=8(cm2).
所以截面BCD的面积为8 cm2.]
二、填空题
6.(一题多空)如图,已知长方体ABCDA1B1C1D1的长、宽、高分别为2,2,1,则长方体的表面积为________,面对角线有________条,体对角线有________条.
16 12 4 [由表面积的定义,可得长方体的表面积为4×1×2+2×2×2=16,面对角线有2×6=12(条),体对角线有4条.]
7.如图,在正方体的8个顶点中任意选择4个顶点,
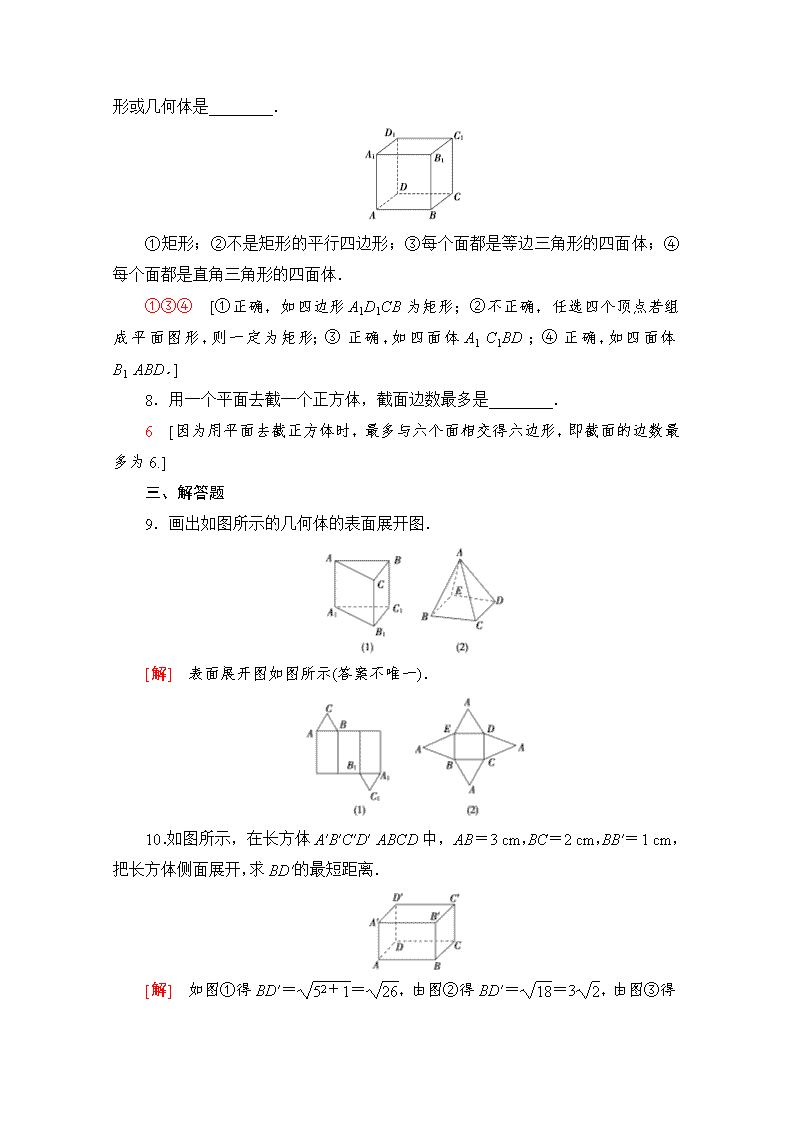
它们可能构成的平面图形或几何体是________.
①矩形;②不是矩形的平行四边形;③每个面都是等边三角形的四面体;④每个面都是直角三角形的四面体.
①③④ [①正确,如四边形A1D1CB为矩形;②不正确,任选四个顶点若组成平面图形,则一定为矩形;③正确,如四面体A1C1BD;④正确,如四面体B1ABD.]
8.用一个平面去截一个正方体,截面边数最多是________.
6 [因为用平面去截正方体时,最多与六个面相交得六边形,即截面的边数最多为6.]
三、解答题
9.画出如图所示的几何体的表面展开图.
[解] 表面展开图如图所示(答案不唯一).
10.如图所示,在长方体A′B′C′D′ABCD中,AB=3 cm,BC=2 cm,BB′=1 cm,把长方体侧面展开,求BD′的最短距离.
[解] 如图①得BD′==,由图②得BD′==3,由图③得BD′==2,
∴(BD′)min=3.
11.五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱对角线的条数共有( )
A.20 B.15 C.12 D.10
D [如图,在五棱柱ABCDEA1B1C1D1E1中,从顶点A出发的对角线有两条:AC1,AD1,同理从B,C,D,E点出发的对角线均有两条,共2×5=10(条).]
12.(多选题)一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是( )
A.三角形 B.四边形 C.五边形 D.六边形
BD [因为正方体容器中盛有一半容积的水,无论怎样转动,其水面总是过正方体的中心,于是过正方体的一条棱和中心可作一截面,截面形状可以是矩形,所以B是正确的;过正方体的一个面相邻两边的中点以及正方体的中心作一截面,得截面形状为正六边形,所以D是正确的;过正方体的中心的平面截正方体得到的截面不可能是三角形和五边形.故选BD.]
13.一个正四棱柱的体对角线的长是9 cm,全面积等于144 cm2,则这个棱柱的侧面积为________ cm2.
112或72 [设底面边长、侧棱长分别为a cm,l cm,
则∴或
∴S侧=4×4×7=112(cm2),
或S侧=4×6×3=72(cm2).]
14.如图所示,在所有棱长均为1的三棱柱上,有一只蚂蚁从点A出发,围着三棱柱的侧面爬行一周到达点A1,则爬行的最短路程为________.
[将三棱柱沿AA1展开如图所示,则线段AD1即为最短路线,即AD1==.
]
15.给出一块正三角形纸片(如图所示),要求将其剪拼成一个底面为正三角形的三棱柱模型,请设计一种剪接方案,并用虚线标示在图中,并作简要说明.
[解] 如图所示,正三角形三个角上剪出三个相同的四边形,其较长的一组邻边边长为三角形边长的,有一组对角为直角,余下部分按虚线三角形的边折成,可成为一个缺上底的底面为正三角形的三棱柱,而剪出的三个相同的四边形恰好拼成这个底面为正三角形的棱柱的上底.
相关文档
- 2020新教材高中物理寒假20天提升作2021-05-06 10:53:373页
- 高中政治:法治政府习题2021-05-06 10:47:145页
- 高中-化学:1物质的量在化学实验中的2021-05-06 10:47:0450页
- 高中化学选修3知识点总结复习过程2021-05-06 10:46:4011页
- 2018-2019学年吉林省长春市九台区2021-05-06 10:45:389页
- 广西省桂梧高中2019-2020学年高一2021-05-06 10:44:3817页
- 2019-2020学年高中物理第1章静电场2021-05-06 10:43:5740页
- 高中同步测试卷·人教物理必修2:高2021-05-06 10:43:347页
- 高中生酒水促销的寒假社会实践报告2021-05-06 10:43:336页
- 2020年上半年高中德育工作总结2021-05-06 10:42:555页