- 808.50 KB
- 2021-04-29 发布
专题七 三角形证明(一)
【中考命题趋势】
常考的知识点包括:全等三角形的判定与性质、线段中垂线的性质、角平分线的性质、等腰三角形的三线合一的性质、直角三角形斜边上的中线的性质、含30°的角的直角三角形的性质等,在中考时,灵活的掌握相应辅助线方法是解决问题的关键.在中考中将会加大对三角形有关证明的考察,而三角形全等是证明的基础.题型主要是以解答题的形式呈现,难度属于中等难度. 线段的和差是中考中常见的考试类型,能较好的考察学生的推理和证明能力,同时能把三角形全等有机的结合起来,因此在最近几年的重庆中考试题中时常出现.针对此类中考热点问题,本专题主要探讨此类问题的解决方法—取长补短法.
【经典专题突破】
第1题图
例1.如图,等边中,是的角平分线,为上一点,以为一边且在下方作等边,连结.
(1)求证:;
(2)延长至, 为上一点,连结、
使, 若时,求的长.
例2.如图,在中,,,为的中点,交于点,交于点,且,过作∥交的延长线于点.
第2题图
(1)求证:;
(2)若,,求线段的长.
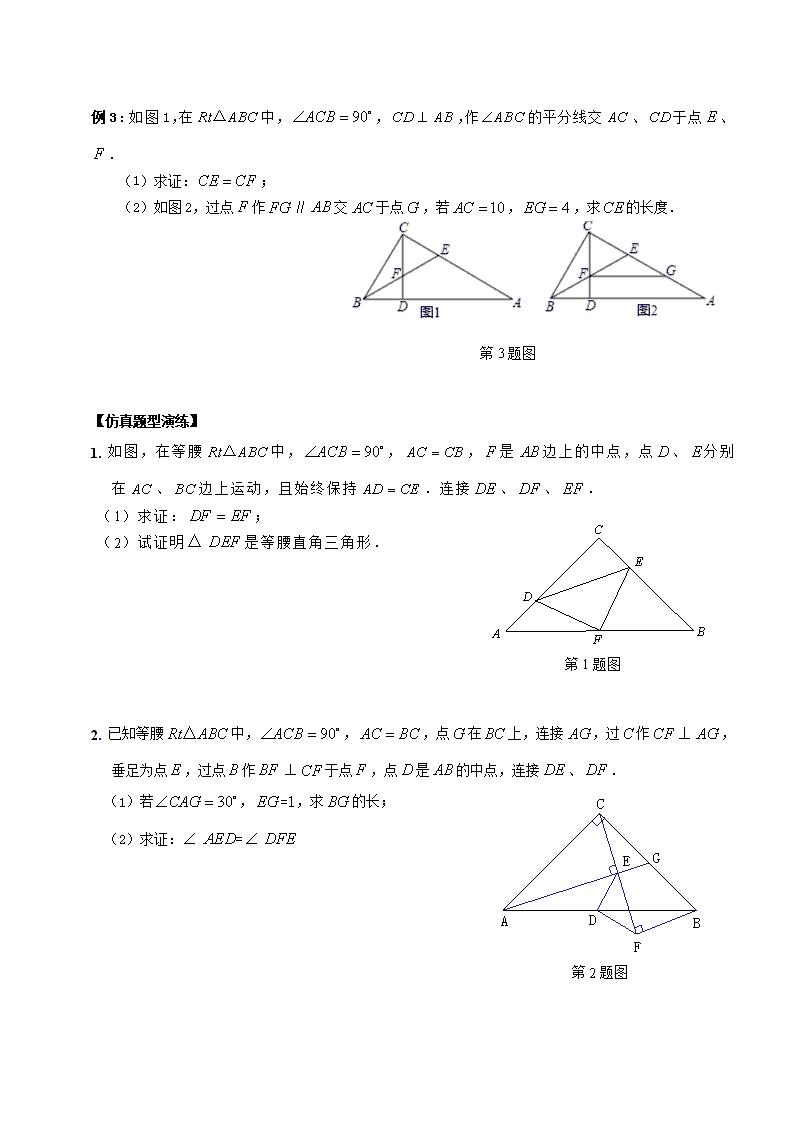
例3:如图1,在中,,,作的平分线交、于点、.
(1)求证:;
(2)如图2,过点作∥交于点,若,,求的长度.
第3题图
【仿真题型演练】
1. 如图,在等腰中,,,是边上的中点,点、分别在、边上运动,且始终保持.连接、、.
第1题图
(1)求证:;
(2)试证明是等腰直角三角形.
2. 已知等腰中,,,点在上,连接,过作,垂足为点,过点作于点,点是的中点,连接、.
第2题图
(1)若,=1,求的长;
(2)求证:=
3. 如图1,已知点为等腰直角内一点,,,为 延长线上的一点,且.
(1)求的大小;
(2)若点在上,如图2,且,求证:.
第3题图
第4题图
4. 如图,在中,,,为上两点,,为 外一点,且,。
(1)证明:;
(2)证明:.
【一线名师预测】
第1题图
1. 如图,在中,,,,垂足分别为为中点,与,分别交于点,,.
(1)证明:;
(2)证明:.
第2题图
2.如图,分别以的边,向外作等边三角形和等边三角形,线段与相交于点,连接.
(1)求的度数;
(2)求证:平分.
三角形证明(二)
【经典专题突破】
第1题图
例1.如图,中,,的角平分线、相交于点,过作交的延长线于点,交于点.
(1)求的度数;
(2)证明:.
例2. 如图,等腰直角三角形中,,、分别为、边上的点,,交于点,过点作交的延长线于点,交于点.
第2题图
(1)证明:为等腰三角形;
(2)证明:.
例3.如图,中,,,点在上,点在延长线上,=,的延长线交于点,连.
(1)证明:;
(2)证明:.
第3题图
【仿真题型演练】
第1题图
1.在四边形中,,,,,是上一点,是延长线上一点,且.
(1)证明:;
(2)在图中,若在上且,
证明:.
2. 如图,是等边的边上一点,是延长线上一点,,连接交 于,过点作于于点.
第2题图
(1)证明:;
(2)证明:.
3. 如图,等边中,点、分别是、的中点,为上一点,连接,作等边,连接,.
(1)若等边的边长为20,且=45°,求等边的边长;
第3题图
(2)证明:.
4. 如图,中,,的角平分线和的外角平分线相交
于点,分别交和的延长线于,.过作交的延长线于点,交的延长线于点,连接交于点.
第4题图
(1)证明:;
(2)证明:;
【一线名师预测】
1.如图,在中,,,,的延长线于.
第1题图
(1)证明:;
(2)若,,求的长度.
2. 如图,已知,是过点的直线,,于点.
第2题图
(1)证明:;
(2)当,时,求的长度.
相关文档
- 2021年三年级数学下册八小数的初步2021-04-29 01:14:5313页
- 安徽省太和中学2019-2020学年高二2021-04-29 01:14:5313页
- 解直角三角形及其应用导学案2021-04-29 01:14:523页
- 2020届二轮复习专题02古代希腊罗马2021-04-29 01:14:3821页
- 江苏省徐州市第一中学2020-2021学2021-04-29 01:14:244页
- 一年级上册数学课件-10以内数的加2021-04-29 01:14:1718页
- 2019-2020学年高中政治部编版必修2021-04-29 01:14:179页
- 四川省武胜烈面中学2019-2020学年2021-04-29 01:14:1613页
- 六年级上册数学教案 百分数的意义 2021-04-29 01:14:093页
- 【语文】湖南省邵阳市洞口第四中学2021-04-29 01:14:0017页