安徽省滁州市定远县育才学校2019-2020学年高二（实验班）上学期期中考试数学（理）试题 11页

育才学校2019-2020学年度第一学期期中 高二实验班理科数学 一、选择题(共12小题,每小题5分,共60分) ‎ ‎1.设点， ，直线过点且与线段相交，则直线的斜率的取值范围是（ ）．‎ A. 或 B. C. D. 或 ‎2.下列命题中正确的个数有 ( )‎ ‎①.‎ ‎②.‎ ‎③两个不重合的平面，两条异面直线，若.‎ ‎④若平面与平行四边形相交于,则.‎ A. 0个 B. 1个 C. 2个 D. 3个 ‎3.已知直线与直线平行，则直线在轴上的截距为（ ）‎ A. B. C. D. ‎ ‎4.某几何体的正视图和侧视图如图（1）所示，它的俯视图的直观图是，如图（2）所示，其中， ，则该几何体的体积为（ ）‎ A. B. C. D. ‎ ‎5.在等腰直角三角形中，，点是边上异于，的一点，光线从点出发，经，反射后又回到点（如图），若光线经过的重心，则等于（ ）‎ A． B． C． D．‎ ‎6.设、是不同的直线， 、、是不同的平面，有以下四个命题：‎ ‎①；②；③；④；其中为真命题的是（ ）．‎ A. ①④ B. ①③ C. ②③ D. ②④‎ ‎7.如图所示，正四棱锥的底面面积为，体积为， 为侧棱的中点，则与所成的角为（ ）‎ A. B. C. D. 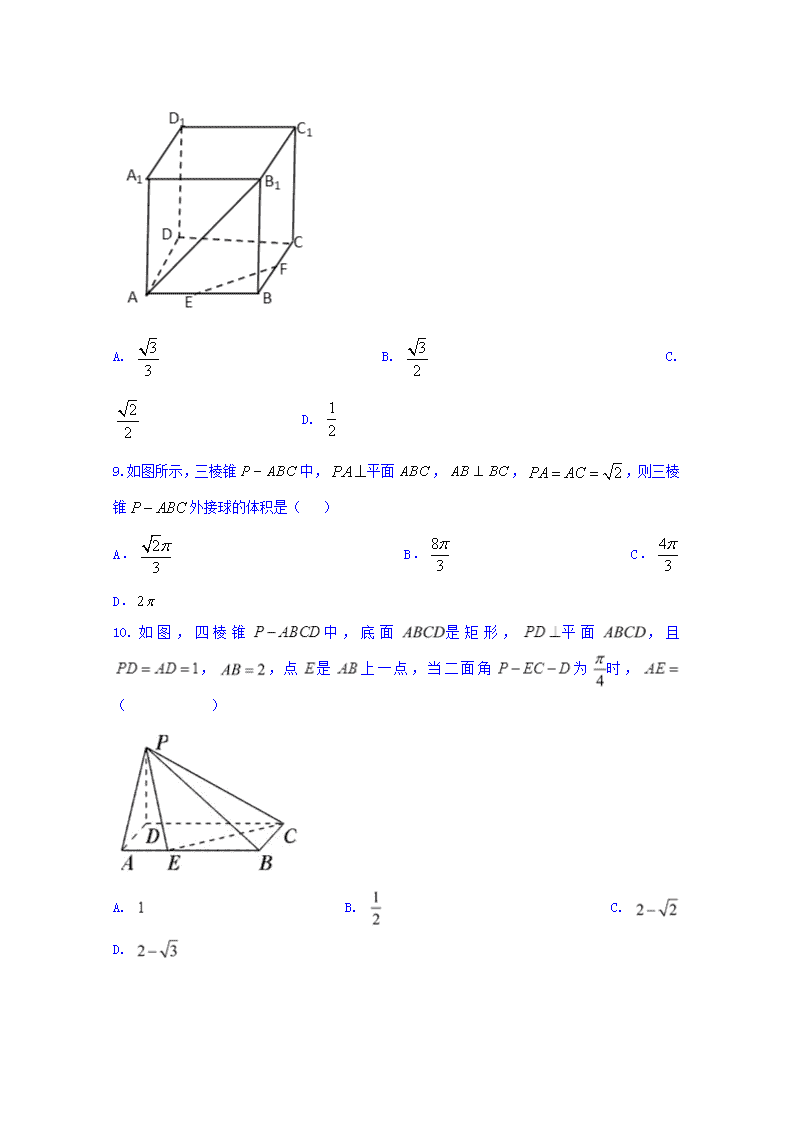‎ ‎8.在正方体中， 分别为的中点，则异面直线所成角的余弦值为 （ ）‎ A. B. C. D. ‎ ‎9.如图所示，三棱锥中，平面，，，则三棱锥外接球的体积是（ ）‎ A． B． C． D．‎ ‎10.如图，四棱锥中，底面是矩形，平面，且，，点是上一点，当二面角为时，（ ）‎ A. B. C. D. ‎ ‎11.某几何体的三视图如图所示，则该几何体的体积为（   ） ‎ A.5 B. C.7 D.‎ ‎12.在正三棱柱中，点为的中点，点是线段上的动点，则关于点到平面的距离说法正确的是（ ）‎ A. 点运动到点时距离最小 B. 点运动到线段的中点时距离最大 C. 点运动到点时距离最大 D. 点到平面的距离为定值 二、填空题(共4小题,共20分) ‎ ‎13.直线：与：互相垂直，则实数 ．‎ ‎14.如图：在边长为的等边三角形中， 与，沿折成二面角后， ，这时二面角的大小为__________．‎ ‎15.在棱长为1的正方体中， 为的中点， 为的中点， 为平面的中心，过作一直线与交于，与交于，则的长为__________．‎ ‎16.点E、F、G分别是正方体ABCD－A1B‎1C1D1的棱AB、BC、B‎1C1的中点，如图所示，则下列命题中的真命题是________(写出所有真命题的编号)．‎ ‎①以正方体的顶点为顶点的三棱锥的四个面中最多只有三个面是直角三角形；‎ ‎②过点F、D1、G的截面是正方形；‎ ‎③点P在直线FG上运动时，总有AP⊥DE；‎ ‎④点Q在直线BC1上运动时，三棱锥A－D1QC的体积是定值；‎ ‎⑤点M是正方体的平面A1B‎1C1D1内的到点D和C1距离相等的点，则点M的轨迹是一条线段．‎ 三、解答题(共6小题,共70分) ‎ ‎17.（12分）点为两直线和的交点．‎ ‎（Ⅰ）求点坐标．‎ ‎（Ⅱ）求过点且与直线平行的直线方程．‎ ‎（Ⅲ）求过原点且与直线和围成的三角形为直角三角形的直线方程．‎ ‎18. （10分）四面体及其三视图如图所示.‎ ‎（1）求四面体的体积； ‎ ‎（2）若点为棱的中点，求异面直线和所成角的余弦值. ‎ ‎19. （12分）已知直线， .‎ ‎（1）当时，直线过与的交点，且它在两坐标轴上的截距相反，求直线的方程；‎ ‎（2）若坐标原点到直线的距离为，判断与的位置关系.‎ ‎20. （12分）在正方体ABCD-A1B‎1C1D中，M为DD1的中点，O为AC的中点，AB=2．‎ ‎（I）求证：BD1∥平面ACM； ‎ ‎（Ⅱ）求证：B1O⊥平面ACM； ‎ ‎（Ⅲ）求三棱锥O-AB‎1M的体积． ‎ ‎21. （12分）如图，在直三棱柱中，是的中点.‎ ‎（1）求证：平面；‎ ‎（2）若，，，求几何体的体积 ‎22. （12分）如图，在四棱锥中，，侧棱，底面为直角梯形，其，为中点.‎ ‎（1）求证：；‎ ‎（2）求异面直线与所成角的余弦值；‎ ‎（3）线段上是否存在，使得它到平面的距离为？若存在，求出的值；若不存在，请说明理由.‎ 参考答案 ‎1.A 2.C 3.B 4.A 5.D 6.B 7.C 8.D 9.C 10.D 11.C 12.D ‎13. 14. 15. 16.③④⑤‎ ‎17.（1）（2）（3）或．‎ 解：（1）解方程组，‎ 可得，‎ ‎∴点坐标为．‎ ‎（Ⅱ）∵直线的斜率为，‎ ‎∴过点的直线为，‎ 即．‎ ‎（或直接设直线为，代入点坐标即可）‎ ‎（Ⅲ）∵的斜率， 的斜率为，‎ 显然， 不是垂直的关系，‎ ‎∴符合条件的直线可以与， 任一直线垂直，‎ ‎∴斜率为或，‎ ‎∴直线方程为或．‎ ‎18.（1）；（2）.‎ 解：（1）根据直角三角形，‎ ‎. ‎ ‎（2）取中点,连，则为与所成角或补角.‎ 则 ‎.‎ 所以异面直线和所成角的余弦值.‎ ‎19.（1）或；（2）或 解：‎ ‎（1）联立解得即与的交点为（021，-9）.‎ 当直线过原点时，直线的方程为；‎ 当直线不过原点时，设的方程为，将（-21，-9）代入得，‎ 所以直线的方程为，故满足条件的直线方程为或.‎ ‎（2）设原点到直线的距离为，‎ 则，解得： 或，‎ 当时，直线的方程为，此时；‎ 当时，直线的方程为，此时.‎ ‎20.（I）证明： ‎ 连结BD，设BD与AC的交点为O， ‎ ‎∵AC，BD为正方形的对角线，故O为BD中点； ‎ 连结MO， ‎ ‎∵O，M分别为DB，DD1的中点， ‎ ‎∴OM∥BD1，…（2分） ‎ ‎∵OM⊂平面ACM，BD1⊄平面ACM…（3分） ‎ ‎∴BD1∥平面ACM． …（4分） ‎ ‎（II）∵AC⊥BD，DD1⊥平面ABCD，且AC⊂平面ABCD， ‎ ‎∴AC⊥DD1；且BD∩DD1=D，∴AC⊥平面BDD1B1…（6分） ‎ OB1⊂平面BDD1B1，∴B1O⊥AC，…（7分） ‎ 连结B‎1M，在△B1MO中 ‎ ‎∴‎ ∴B1O⊥OM…（10分） ‎ 又OM∩AC=O，∴B1O⊥平面AMC； …（11分） ‎ ‎．（II） V=‎ ‎21.‎ ‎（1）证明：连接，与交于点O，连接DO 由直三棱柱性质可知，侧棱垂直于底面，侧面为矩形，‎ 所以O为中点，‎ 则 又因为平面，平面，‎ 所以：平面；‎ ‎（2）.‎ ‎22. （1）证明：在中，为中点，所以.‎ 又，‎ 所以.‎ ‎（2）解：连接，在直角梯形中，，‎ 有且，所以四边形是平行四边形，‎ 所以.‎ 由（1）知，为锐角，‎ 所以是异面直线与所成的角.‎ 因为，在中，，所以，‎ 在中，因为，所以，‎ 在中，，所以，‎ 所以异面直线与所成的角的余弦值为.‎ ‎（3）解：假设存在点，使得它到平面的距离为.‎ 设，则，由（2）得，‎ 在中，，‎ 所以，‎ 由得，所以存在点满足题意，此时.‎