2017-2018学年江苏省泰州中学高二下学期4月月考数学理试题（Word版） 10页

‎2017-2018学年江苏省泰州中学高二下学期4月月考数学理试题 第Ⅰ卷 一、填空题（将答案填在答题纸上）‎ ‎1. 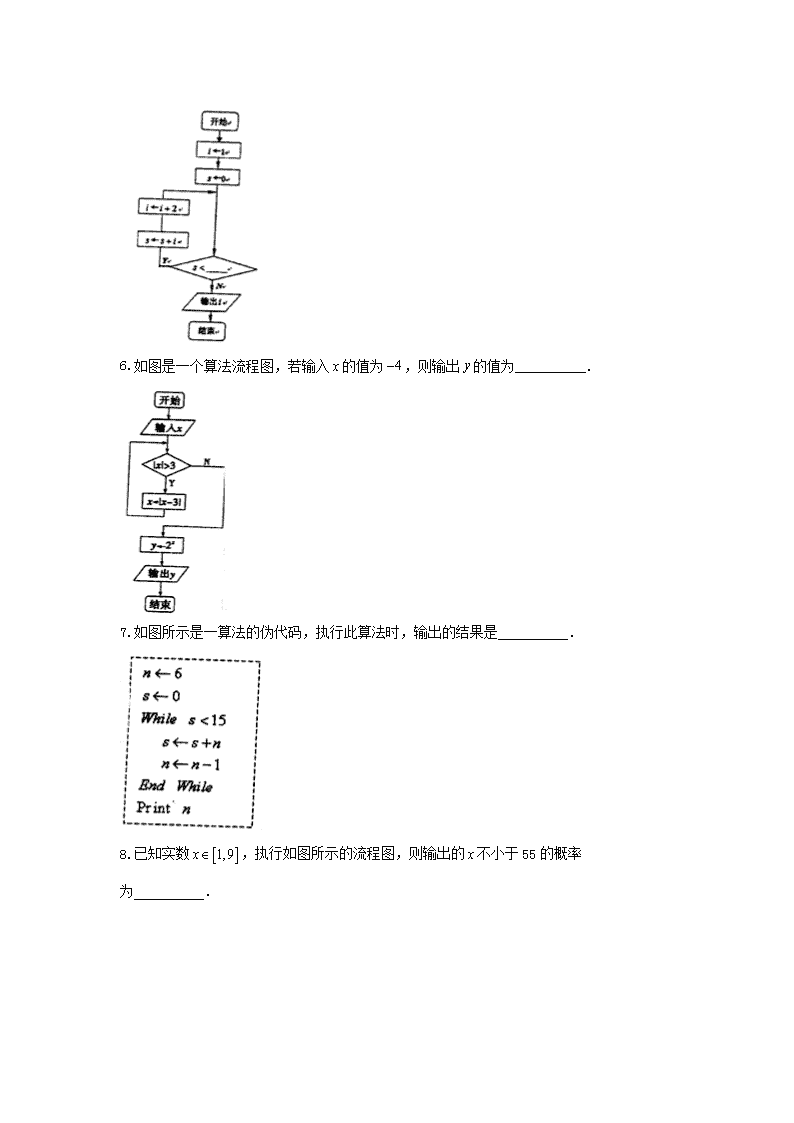总体由编号为的50各个体组成，利用随机数表（以下摘取了随机数表中第1行和第2行）选取5个个体，选取方法是从随机数表第1行的第9列和第10列数字开始由左向右读取，则选出来的第4个个体的编号为 ．‎ ‎66 67 40 67 14 64 05 71 95 86 11 05 65 09 68 76 83 20 37 90‎ ‎57 16 00 11 66 14 90 84 45 11 75 73 88 05 90 52 27 41 14 86‎ ‎2.已知某人连续5次投掷飞镖的环数分别是8,9,10,10,8，则该组数据的方差为 ．‎ ‎3.已知为坐标原点，，若，则的坐标是 ．‎ ‎4.一个社会调查机构就某地居民的月收入调査了10000人，并根据所得数据画出了如图所示的频率分布直方图，现要从这10000人中再用分层抽样的方法抽出100人作进一步调査，则月收入在 (元）内应抽出 人.‎ ‎5.如图所示的流程图，若输出的结果是15，则判断框中的横线上可以填入的最大整数为 ．‎ ‎6.如图是一个算法流程图，若输入的值为，则输出的值为 ．‎ ‎7.如图所示是一算法的伪代码，执行此算法时，输出的结果是 ．‎ ‎8.已知实数，执行如图所示的流程图，则输出的不小于55的概率为 ．‎ ‎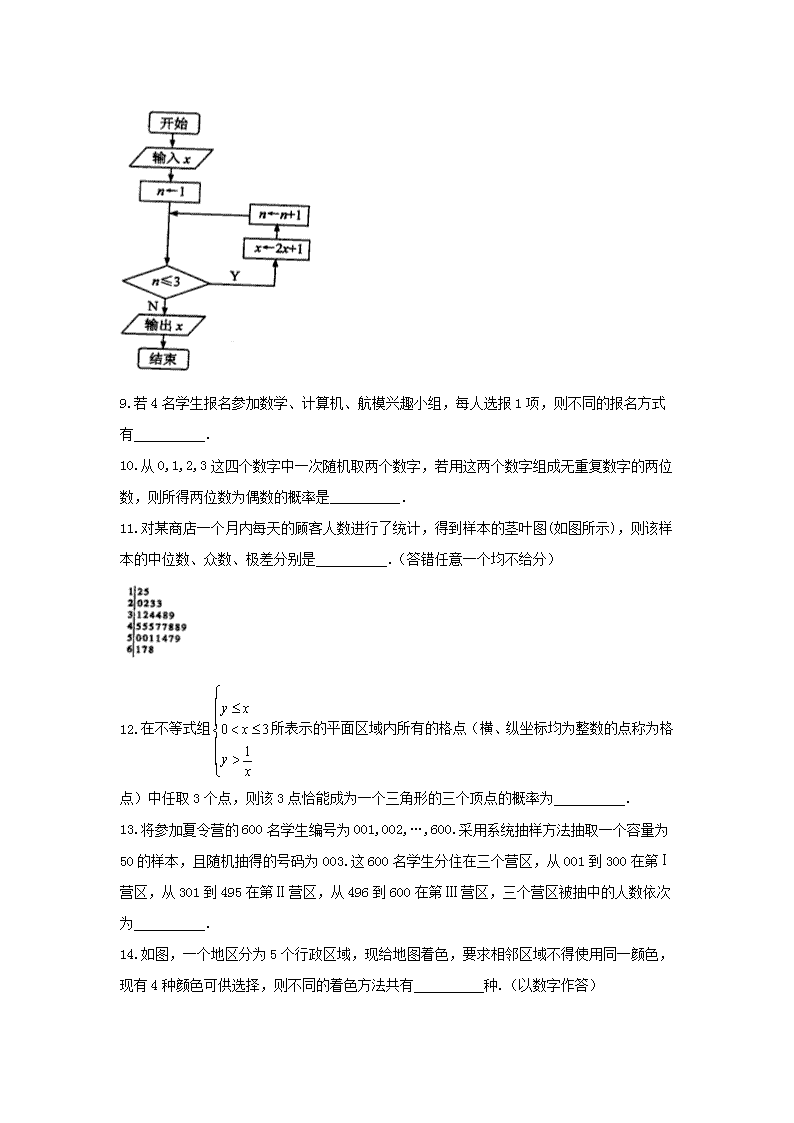9.若4名学生报名参加数学、计算机、航模兴趣小组，每人选报1项，则不同的报名方式有 ．‎ ‎10.从0,1,2,3这四个数字中一次随机取两个数字，若用这两个数字组成无重复数字的两位数，则所得两位数为偶数的概率是 ．‎ ‎11.对某商店一个月内每天的顾客人数进行了统计，得到样本的茎叶图(如图所示)，则该样本的中位数、众数、极差分别是 ．（答错任意一个均不给分）‎ ‎12. 在不等式组所表示的平面区域内所有的格点（横、纵坐标均为整数的点称为格点）中任取3个点，则该3点恰能成为一个三角形的三个顶点的概率为 ．‎ ‎13.将参加夏令营的600名学生编号为001,002,…,600.采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003.这600名学生分住在三个营区，从001到300在第营区，从301到495在第营区，从496到600在第营区，三个营区被抽中的人数依次为 ．‎ ‎14.如图，一个地区分为5个行政区域，现给地图着色，要求相邻区域不得使用同一颜色，现有4种颜色可供选择，则不同的着色方法共有 种.（以数字作答）‎ 第Ⅱ卷 二、解答题 （解答应写出文字说明、证明过程或演算步骤.） ‎ ‎15.某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是.‎ ‎（1）求图中的值；‎ ‎（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；‎ ‎（3）若这100名学生语文成绩某些分数段的人数与数学成绩相应分数段的人数之比如下表所示，求数学成绩在之外的人数.‎ ‎16.某超市为了了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示.‎ 已知这100位顾客中一次购物量超过8件的顾客占.‎ ‎（1）确定的值，并估计顾客一次购物的结算时间的平均值；‎ ‎（2）求一位顾客一次购物的结算时间不超过2.5分钟的概率.（将频率视为概率)‎ ‎17．如图，在四棱锥中，底面是矩形，垂直于底面，，点为线段(不含端点）上一点.‎ ‎（1）当是线段的中点时，求与平面所成角的正弦值；‎ ‎（2）已知二面角的正弦值为，求的值.‎ ‎18.已知关于的一次函数.‎ ‎（1）设集合和，分别从集合和中随机取一个数作为和，求函数是增函数的概率；‎ ‎（2）实数满足条件，求函数的图象经过第一、二、三象限的概率.‎ ‎19.如图，圆锥的高，底面半径，为的中点，为母线的中点，为底面圆周上一点，满足.‎ ‎（1）求异面直线与所成角的余弦值；‎ ‎（2）求二面角的正弦值.‎ ‎20.如图，在三棱柱中，平面，，且.‎ ‎（1）求棱与所成的角的大小；‎ ‎（2）在棱上确定一点，使二面角的平面角的余弦值为.‎ 试卷答案 一、填空题 ‎1. 09 2. 3. 4. 25‎ ‎5. 49 6. 2 7. 3 8. ‎ ‎9. 81 10. 11. 46,45,56 12. ‎ ‎13. 25,17,8 14. 72 ‎ 二、解答题 ‎15. 解（1）由频率分布直方图知，解得.‎ ‎（2）由频率分布直方图知这100名学生语文成绩的平均分为（分）‎ ‎（3）由频率分布直方图知语文成绩在各分数段的人数依次为，，，.‎ 由题中给出的比例关系知数学成绩在上述各分数段的人数依次为5，，，.‎ 故数学成绩在之外的人数为.‎ ‎16.（1） 由已知得，，∴， 该超市所有顾客一次购物的结算时间组成一个总体， 所收集的100位顾客一次购物的结算时间可视为一个容量为100的简单随机样本， 顾客一次购物的结算时间的平均值可用样本平均数估计， 其估计值为：（分钟）.‎ ‎（2）记为“一位顾客一次购物的结算时间不超过2.5分钟”，分别表示事件1分钟”， 1.5分钟”， 2分钟，2.5分钟”，将频率视为概率，得，，，，‎ ‎∵，且是互斥事件，‎ ‎∴， 故一位顾客一次购物的结算时间不超过2.5分钟的概率为.‎ ‎17.（1）以为原点,为坐标轴,建立如图所示空间直角坐标系：设, ‎ 则；‎ 所以，‎ 设平面的法向量，则，‎ 即，解得，所以平面的一个法向量，‎ ‎，‎ 则与平面所成角的正弦值为.‎ ‎（2）由（1）知平面的一个法向量为，设，则，，，设平面的法向量，则，即，解得，所以平面的一个法向量，‎ 由题意得，‎ 所以，即，‎ 因为，所以，则.‎ ‎18.解（1）抽取的全部结果的基本事件有，共10个基本事件，设使函数为增函数的事件为，则包含的基本事件有，共 6 个基本事件，所以，‎ ‎.‎ ‎（2）满足条件的区域如图所示.‎ 要使函数的图象过第一、二、三象限，则，故使函数图象过第一、二、三象限的的区域为第一象限的阴影部分，∴所求事件的概率为.‎ ‎19.（1）以为原点，底面上过点且垂直于的直线为轴，所在的线为轴，所在的线为轴，建立空间直角坐标系，则 ‎，‎ 设，且，‎ 则，，‎ ‎∵，即，则，故.‎ ‎∴.‎ 设异面直线与所成角为，则.‎ ‎（2）设平面的法向量为，则即，‎ 令，得，平面的一个法向量为.‎ 设平面的法向量为，‎ 同理可得平面的法向量为.‎ 设二面角的平面角为，则.‎ ‎∴.‎ ‎20.解（1）如图，以为原点建立空间直角坐标系，‎ 则，‎ ‎.‎ ‎，‎ 故与棱所成的角是.‎ ‎（2）为棱中点，‎ 设，则.‎ 设平面的法向量为，，‎ 则，‎ 故 而平面的法向量是，则，‎ 解得，即为棱中点，其坐标为. ‎