四川省泸州市2020届高三第三次教学质量诊断性考试数学（理）试题 18页

泸州市高2017级第三次教学质量诊断性考试 数学（理科）‎ 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至2页，第Ⅱ卷3至4页．共150分．考试时间120分钟．‎ 注意事项：‎ ‎1．答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置．‎ ‎2．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题的答案标号涂黑．‎ ‎3．填空题和解答题的作答：用签字笔直接答在答题卡上对应的答题区域内，作图题可先用铅笔绘出，确认后再用0.5毫米黑色签字笔描清楚，写在试题卷、草稿纸和答题卡上的非答题区域均无效．‎ ‎4．考试结束后，请将本试题卷和答题卡一并上交．‎ 第Ⅰ卷（选择题 共60分）‎ 一、选择题：本大题共有12个小题，每小题5分，共60分．每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．设集合，，则（ ）．‎ A． B． C． D．‎ ‎2．若，则（ ）．‎ A． B． C． D．‎ ‎3．展开式中项的系数为（ ）．‎ A．10 B．5 C． D．‎ ‎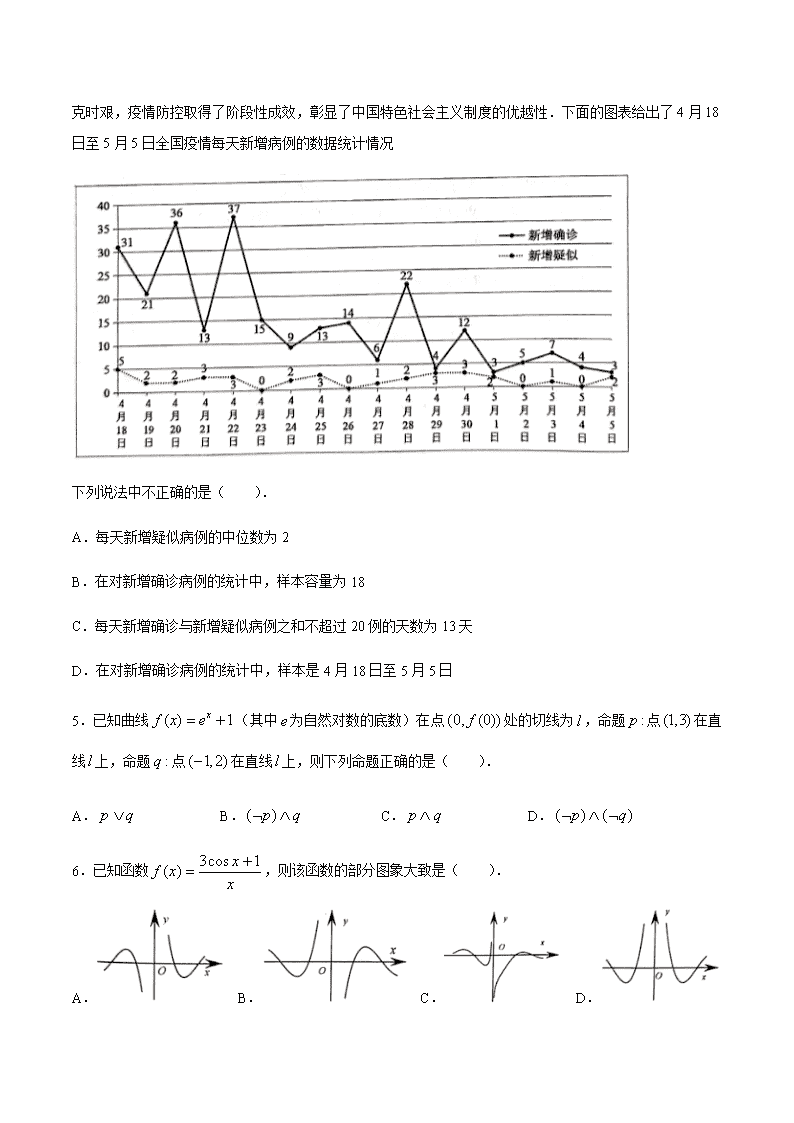4．新冠肺炎疫情暴发以来，在以习近平同志为核心的党中央领导下，全党全军全国各族人民众志成城，共克时艰，疫情防控取得了阶段性成效，彰显了中国特色社会主义制度的优越性．下面的图表给出了4月18日至5月5日全国疫情每天新增病例的数据统计情况 下列说法中不正确的是（ ）．‎ A．每天新增疑似病例的中位数为2‎ B．在对新增确诊病例的统计中，样本容量为18‎ C．每天新增确诊与新增疑似病例之和不超过20例的天数为13天 D．在对新增确诊病例的统计中，样本是4月18日至5月5日 ‎5．已知曲线（其中为自然对数的底数）在点处的切线为，命题点在直线上，命题点在直线上，则下列命题正确的是（ ）．‎ A． B． C． D．‎ ‎6．已知函数，则该函数的部分图象大致是（ ）．‎ A． B． C． D．‎ ‎7．等差数列的公差不为零，其前项和为，若，则的值为（ ）．‎ A．15 B．20 C．25 D．40‎ ‎8．某中学高二学生会体育部共有5人，现需从体育部选派4人，分别担任拔河比赛的裁判、记录结果、核查人数、维持纪律四项工作，每人只担任其中一项工作，其中甲没有担任裁判工作，则不同的工作安排方式共有（ ）．‎ A．120种 B．48种 C．96种 D．60种 ‎9．正方体中，下列命题中正确的是（ ）．‎ A．与是相交直线且垂直 B．与是异面直线且垂直 C．与是相交直线且垂直 D．与是异面直线且垂直 ‎10．定义在实数集上的函数满足，且当时，是增函数，则，，的大小关系正确的是（ ）．‎ A． B． C． D．‎ ‎11．已知点为抛物线的焦点，过点的直线交于，两点，与的准线交于点，若，则的值等于（ ）．‎ A． B． C． D．‎ ‎12．已知曲线，把上各点横坐标伸长为原来的2倍，纵坐标不变，得到函数 的图象，关于有下述四个结论：‎ ‎（1）函数在上是减函数；‎ ‎（2）方程在内有2个根；‎ ‎（3）函数（其中）的最小值为；‎ ‎（4）当，且时，，则．‎ 其中正确结论的个数为（ ）．‎ A．1 B．2 C．3 D．4‎ 第Ⅱ卷（非选择题 共90分）‎ 注意事项：‎ ‎（1）非选择题的答案必须用0.5毫米黑色签字笔直接答在答题卡上，作图题可先用铅笔绘出，确认后再用0.5毫米黑色签字笔描清楚，答在试题卷和草稿纸上无效．‎ ‎（2）本部分共10个小题，共90分．‎ 二、填空题（本大题共4小题，每小题5分，共20分．把答案填在答题纸上）‎ ‎13．已知平面向量与满足，且，则________．‎ ‎14．已知正项等比数列的前项和为，若，，则该数列的公比为________．‎ ‎15．已知双曲线的焦距为，且它的渐近线与圆有交点，连接所有交点的线段围成了几何图形，则该几何图形的面积为________．‎ ‎16．已知一块边长为4的正方形铝板（如图）‎ ‎，请设计一种裁剪方法，用虚线标示在答题卡本题图中，通过该方案裁剪，可焊接做成一个密封的正四棱柱（底面是正方形且侧棱垂于底面的四棱柱），且该四棱柱的全面积等于正方形铝板的面积（要求裁剪的块数尽可能少，不计焊接缝的面积），则该四棱柱外接球的体积为________（画虚线2分，外接球的体积3分）．‎ 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．‎ ‎（一）必考题：共60分．‎ ‎17．（本题满分12分）‎ 某省从2021年开始，高考采用取消文理分科，实行“”的模式，其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目．某校高一年级有2000名学生（其中女生900人）．该校为了解高一年级学生对“1”的选课情况，采用分层抽样的方法抽取了200名学生进行问卷调查，下表是根据调查结果得到的列联表．‎ 性别 选择物理 选择历史 总计 男生 ‎________‎ ‎50‎ 女生 ‎30‎ ‎________‎ 总计 ‎________‎ ‎________‎ ‎200‎ ‎（Ⅰ）求，的值；‎ ‎（Ⅱ）请你依据该列联表判断是否有99.5%的把握认为选择科目与性别有关？说明你的理由．‎ ‎0.100‎ ‎0.050‎ ‎0.025‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 附：，其中．‎ ‎18．（本题满分12分）‎ 在中，角，，所对的边分别为，，，且．‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）若，边上的中线的长为1，求的面积．‎ ‎19．（本题满分12分）‎ 如图，四棱锥的侧面是正三角形，，且，，是中点．‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）若平面平面，且，求二面角的余弦值．‎ ‎20．（本题满分12分）‎ 在平面直角坐标系中，直线交椭圆于两点，．‎ ‎（Ⅰ）若，且点满足，证明：点不在椭圆上；‎ ‎（Ⅱ）若椭圆的左，右焦点分别为，，直线与线段和椭圆的短轴分别交于两个不同点，‎ ‎，且，求四边形面积的最小值．‎ ‎21．（本题满分12分）‎ 已知函数．‎ ‎（Ⅰ）求函数的单调增区间；‎ ‎（Ⅱ）函数，当时，恒成立，求整数的最小值．‎ ‎（二）选考题：共10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分．‎ ‎22．（本题满分10分）选修4-4：坐标系与参数方程 数学中有许多形状优美、寓意美好的曲线，如下图就是在平面直角坐标系的“茹茹心形曲线”，又名RC心形线．如果以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，其RC心形线的极坐标方程为．‎ ‎（Ⅰ）求RC心形线的直角坐标方程；‎ ‎（Ⅱ）已知与直线（为参数），若直线与RC心形线交于两点，，求的值．‎ ‎23．（本题满分10分）选修4-5：不等式选讲 已知的最小值为．‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）当时，证明：．‎ 泸州市高2017级第三次教学质量诊断性考试 数学（理科）参考答案 评分说明：‎ ‎1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分参考制订相应的评分细则．‎ ‎2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度．可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．‎ ‎3．解答右侧所注分数，表示考生正确做到这一步应得的累加分数．‎ ‎4．只给整数分数．选择题和填空题不给中间分．‎ 一、选择题：‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B D C D A A B C D C D C 二、填空题：‎ ‎13．3 14． 15．16‎ ‎16．；．或；．或；；等．‎ 三、解答题：‎ ‎17．解：（Ⅰ）根据题意得，‎ ‎ 3分 解得， 4分 所以女生人数为； 6分 ‎（Ⅱ）列联表如下：‎ 性别 选择物理 选择历史 总计 男生 ‎60‎ ‎50‎ ‎110‎ 女生 ‎30‎ ‎60‎ ‎90‎ 总计 ‎90‎ ‎110‎ ‎200‎ 计算 ‎， 9分 所以有99.5%的把握认为选择科目与性别有关． 12分 ‎18．解：（Ⅰ）由正弦定理得， 1分 所以， 2分 则， 3分 又因为， 4分 所以，， 5分 所以； 6分 ‎（Ⅱ）方法一：由题意知，在中，有，‎ 则， 7分 平方得， 9分 所以， 10分 即， 11分 所以的面积为． 12分 ‎（Ⅱ）方法二：由题得，① 7分 ‎，即，② 8分 ‎，即，③ 9分 由②③得，④ 10分 由①④得， 11分 所以的面积为． 12分 ‎19．解：（Ⅰ）取的中点，连接，‎ 因为是中点，‎ 所以，且， 1分 又因为，，‎ 所以，， 2分 即四边形是平行四边形， 3分 所以， 4分 又因为平面，平面，‎ 所以平面； 5分 ‎（Ⅱ）方法一：取中点，连接，，‎ 因为是正三角形，所以，‎ 因为平面平面，‎ 所以平面，平面， 7分 所以，‎ 故， 8分 以为原点，建立如图所示的空间直角坐标系，则，‎ ‎，，，，，， 9分 所以，，‎ 设平面的法向量为，则，，‎ 令得， 10分 易知平面的法向量为， 11分 则，‎ 所以二面角的余弦值为． 12分 方法二：过作交于，‎ 所以，且平面， 7分 过作交于，连接，‎ 所以， 8分 所以为二面角的平面角， 9分 因为，，‎ 因为平面，‎ 所以，且， 10分 又因为，所以，， 11分 故，所以二面角的余弦值为． 12分 ‎20．解：设直线交椭圆于两点，，‎ ‎（Ⅰ）把代入得，‎ 所以，， 1分 因为，‎ 所以 ‎， 2分 因为， 3分 所以点不在椭圆上； 4分 ‎（Ⅱ）由代入得，‎ 则，，‎ 又，， 5分 因为，所以，即，‎ 所以， 6分 因为直线与线段及椭圆的短轴分别交于不同两点，‎ 所以，‎ 又，则，‎ 故，， 7分 ‎，即， 8分 因为，，‎ 所以 ‎， 9分 因为 ‎， 10分 所以， 11分 故当或时，四边形面积的最小值为． 12分 ‎21．解：（Ⅰ）因为， 1分 当时，，所以函数的单调递增区间是； 2分 当时，由得，‎ 所以函数的单调增区间是； 3分 当时，由得，‎ 所以函数的单调递增区间是； 4分 方法一：（Ⅱ）因为，即，因为，‎ 所以，令，‎ 所以， 5分 设，‎ 则， 6分 所以且时，，‎ 故在上是增函数， 7分 因为，‎ 当时，‎ ‎．‎ 所以存在使， 8分 所以当时，即，‎ 当时，即，‎ 所以在上增函数，上是减函数， 9分 故有最大值为 ‎ 10分 ‎， 11分 因为，，所以，‎ 故，即整数的最小值为2． 12分 方法二：（Ⅱ）因为，即，因为，‎ 所以，令， 5分 ‎（1）当时，因为，所以，‎ 因此，所以只需； 6分 ‎（2）当时，因为，则，‎ 所以，‎ 因此只需，即，‎ 构造函数， 7分 ‎， 8分 当时，在上单调递减，； 9分 当时，，‎ 则，不满足题意； 10分 当时，，‎ 则，故不满足题意； 11分 综上可知，整数的最小值为2． 12分 ‎22．解：（Ⅰ）因为，所以， 1分 即， 3分 故； 4分 ‎（Ⅱ）因为在直线（为参数）上， 5分 设直线的参数方程为（为参数） 6分 若直线与RC心形线交于两点，，‎ 则只能交于轴右侧部分， 7分 将其代入方程得， 8分 所以． 10分 ‎23．解：（Ⅰ）因为，‎ 所以， 2分 所以． 4分 ‎（Ⅱ）方法一：因为，‎ 所以 ‎， 5分 所以要证明，即证明． 6分 因为 7分 ‎，证 8分 所以． 9分 因为，所以，‎ 所以． 10分 方法二：由柯西不等式有 ‎ 7分 所以， 8分 故． 10分