- 1.79 MB
- 2021-04-28 发布
广东省中山市2020届高三上学期期末考试数学试题(文)
一、选择题:本大题共12题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.集合,,则( )
A. B.
C. D.
【答案】D
【解析】由题意得,
∴.选D.
2.已知是虚数单位,复数满足,则( )
A. B. C. D. 5
【答案】A
【解析】依题意,
所以.
故选:A.
3.计算的结果为( )
A. B. C. D.
【答案】B
【解析】
所以选B.
4.“”是直线与圆相切的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
【答案】C
【解析】由圆,可得圆心为,半径.
∵直线与圆相切,∴,∴,∴“”是直线与圆相切的充要条件,故选C.
5.下列四个正方体图形中,,为正方体的两个顶点,,,分别为其所在棱的中点,能得出平面的图形的序号是( )
A. ①③ B. ②③ C. ①④ D. ②④
【答案】C
【解析】对于①,连接如图所示,由于,根据面面平行的性质定理可知平面平面,所以平面.
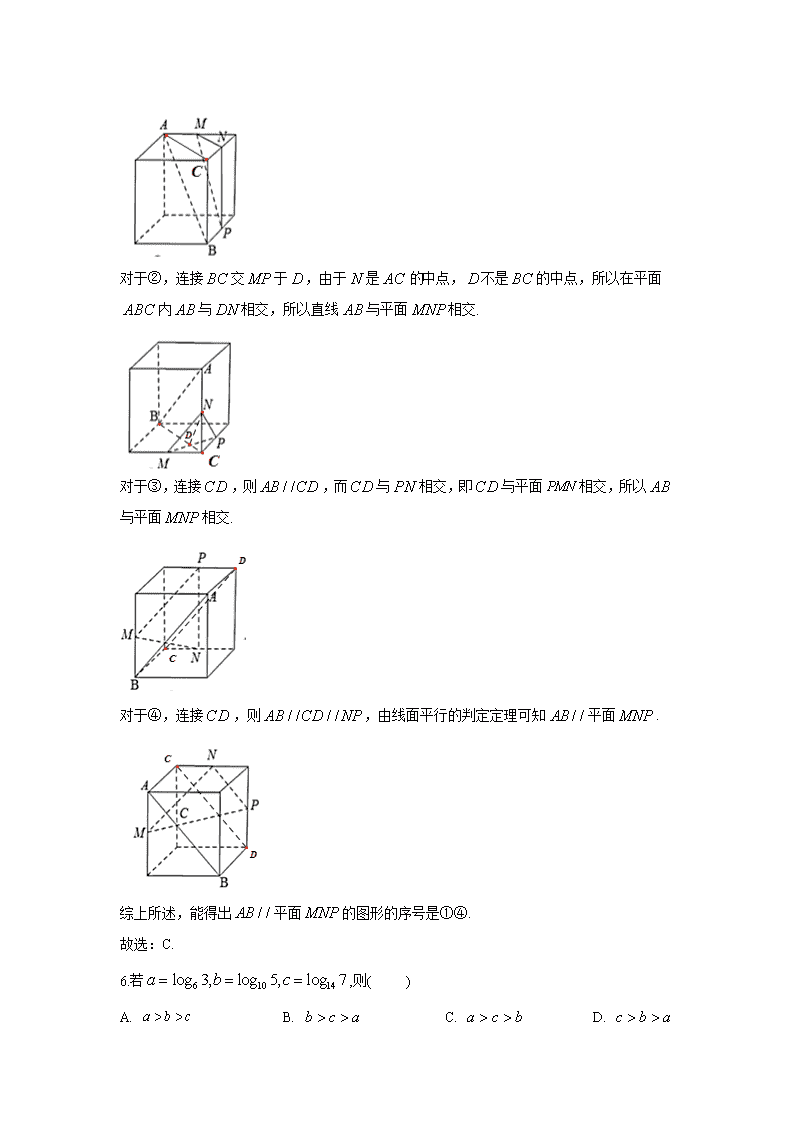
对于②,连接交于,由于是中点,不是的中点,所以在平面内与相交,所以直线与平面相交.
对于③,连接,则,而与相交,即与平面相交,所以与平面相交.
对于④,连接,则,由线面平行的判定定理可知平面.
综上所述,能得出平面的图形的序号是①④.
故选:C.
6.若,则( )
A. B. C. D.
【答案】D
【解析】,,,
令,则在上是单调增函数.
又,所以
即.故选D.
7.下图是某公司2018年1月至12月空调销售任务及完成情况的气泡图,气泡的大小表示完成率的高低,如10月份销售任务是400台,完成率为90%,则下列叙述不正确的是( )
A. 2018年3月的销售任务是400台
B. 2018年月销售任务的平均值不超过600台
C. 2018年第一季度总销售量为830台
D. 2018年月销售量最大的是6月份
【答案】D
【解析】对于选项A,由图可得3月份的销售任务是400台,所以A正确.
对于选项B,由图形得2018年月销售任务的平均值为
,所以B正确.
对于选项C,由图形得第一季度的总销售量为台,所以C正确.
对于选项D,由图形得销售量最大的月份是5月份,为800台,所以D不正确.
故选D.
8.已知满足不等式组则的最小值为( )
A. 2 B. C. D. 1
【答案】D
【解析】不等式组对应的可行域如图所示,
因为所以z表示可行域内一点到直线x+y-1=0距离的倍,由可行域可知点A(2,0)到直线x+y-1=0的距离最短,故故选D.
点睛:本题的关键是找到的几何意义,要找到的几何意义,必须变形,所以z表示可行域内一点到直线x+y-1=0距离的倍.突破了这一点,后面的解答就迎刃而解了.
9.已知函数的最小正周期是,若,则( )
A. B. C. 1 D. -1
【答案】D
【解析】由于的最小正周期为,所以,所以.所以.由得.所以
.
故选:D.
10.我国古代数学名著《九章算术》中有这样一些数学用语,“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,而“阳马”指底面为矩形,且有一侧棱垂直于底面的四棱锥.现有一如图所示的堑堵,,若,当阳马体积最大时,则堑堵的外接球体积为( )
A. B. C. D.
【答案】B
【解析】依题意可知平面.设,则.,当且仅当时取得最大值.依题意可知是以为斜边的直角三角形,所以堑堵外接球的直径为,故半径.所以外接球的体积为.
特别说明:由于平面,是以为斜边的直角三角形,所以堑堵外接球的直径为为定值,即无论阳马体积是否取得最大值,堑堵外接球保持不变,所以可以直接由直径的长,计算出外接球的半径,进而求得外接球的体积.
故选:B.
11.已知数列是各项均为正数的等比数列,为数列的前项和,若,则的最小值为( )
A. 9 B. 12 C. 16 D. 18
【答案】D
【解析】由得,所以.所以.当且仅当时取得最小值.
故选:D.
12.已知函数(其中无理数),关于的方程有四个不等的实根,则实数的取值范围是( )
A. B.
C. D.
【答案】C
【解析】依题意可知函数的定义域为.且
.所以在上递增,在上递减,且,由此画出的图像如下图所示.
令,则的单调性与相同,且.
关于的方程有四个不等的实根,所以,即在上各有一实根.令,所以,即,所以.所以实数的取值范围是.
故选:C
二、填空题:本大题共4题,每小题5分,共20分,请将答案填在答题卡对应题号的位置上,答错位置,书写不清,模棱两可均不得分.
13.等差数列的前项和为,若,是方程的两根,则:__________.
【答案】52
【解析】由于,是方程的两根,所以,所以.
故答案为:.
14.如图所示,已知正方形,以对角线为一边作正,现向四边形区域内投一点,则点落在阴影部分的概率为__________.
【答案】
【解析】设正方形的边长为2,则.
∵为正三角形
∴
∴阴影部分面积为
∴向四边形区域内投一点,则点落在阴影部分的概率为
故答案为.
15.已知向量与的夹角是,且,则向量与的夹角是_____.
【答案】
【解析】由两边平方并化简得,即,即.所以,由于,所以.
故答案为:.
16.已知函数,若有,则实数取值范围是__________.
【答案】
【解析】∵,
∴函数在R上为增函数,
由题意得,
∴,
∵,
∴.
∴,解得.
∴实数的取值范围是.
三、解答题:本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤.
17.设为数列的前项和,已知,.
(1)证明为等比数列;
(2)判断,,是否成等差数列?并说明理由.
(1)证明:∵,,∴,
由题意得,,
∴是首项为2,公比为2的等比数列.
(2)解:由(1),∴.
∴,
∴,
∴,即,,成等差数列.
18.为检查某工厂所生产的8万台电风扇的质量,抽查了其中20台的无故障连续使用时限(单位:小时) 如下:
248 256 232 243 188 268 278 266 289 312
274 296 288 302 295 228 287 217 329 283
分组
频数
频率
频率/组距
总计
0.05
(1)完成频率分布表,并作出频率分布直方图;
(2)估计8万台电风扇中有多少台无故障连续使用时限不低于280小时;
(3)用组中值(同一组中的数据在该组区间的中点值)估计样本的平均无故障连续使用时限.
解:(1)频率分布表及频率分布直方图如下所示:
分组
频数
频率
频率/组距
1
0.05
0.0025
1
0.05
0.0025
2
0.10
0.0050
3
0.15
0.0075
4
0.20
0.0100
6
0.30
0.0150
2
0.10
0.0050
1
0.05
0.0025
总计
20
1.00
0.05
(2)(万).
答:估计8万台电扇中有3.6万台无故障连续使用时限不低于280小时.
(3)(小时).
答:样本的平均无故障连续使用时限为269小时.
19.已知的三个内角,,所对的边分别为,,.
(1)若,求;
(2)若,试判断的形状.
解:(1)∵,
∴,,
∴,
∴,
∴,
∴或(舍去),
∴,
∴.
(2)∵,
∴,,
∴或,,为锐角.
∴(舍去),
∴,
∴为直角三角形.
20.如图1,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图2所示的四棱锥D1—ABCE,其中平面D1AE⊥平面ABCE.
(1)证明:BE⊥平面D1AE;
(2)设F为CD1的中点,在线段AB上是否存在一点M,使得MF∥平面D1AE,若存在,求出的值;若不存在,请说明理由.
解:(1)证明连接BE,
∵ABCD为矩形且AD=DE=EC=BC=2,
∴∠AEB=90°,即BE⊥AE,
又平面D1AE⊥平面ABCE,
平面D1AE∩平面ABCE=AE,BE⊂平面ABCE,
∴BE⊥平面D1AE.
(2)解AM=AB,取D1E的中点L,连接AL,FL,
∵FL∥EC,EC∥AB,∴FL∥AB且FL=AB,
∴FL∥AM,FL=AM
∴AMFL为平行四边形,∴MF∥AL,
因为MF不在平面AD1E上, AL⊂平面AD1E,所以MF∥平面AD1E.
故线段AB上存在满足题意的点M,且=.
21.已知函数,其中为自然对数的底数.
(1)求函数的最小值;
(2)若都有,求证:.
解:(1)∵,∴,
∴当时,,函数单调递减,
当时,,函数单调递增,
∴.
(2)证明:∵,都有,
∴即,
设,,
∴,
令,,∴,∴在上单调递增,
∵,,∴存在唯一使得,
∴当时,,函数单调递增,
当时,,函数单调递减,
∴,
∵,,
∴即,
∴,
令,,
∵,
∴上单调递增,∴,
∵,,
∴.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
选修4-4:坐标系与参数方程
22.在直角坐标系中,曲线经过伸缩变换后得到曲线.以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(1)求曲线的参数方程;
(2)若分别是曲线上的动点,求的最大值.
解:(1)曲线经过伸缩变换,可得曲线的方程为,
∴其参数方程为为参数);
曲线的极坐标方程为,即,
∴曲线的直角坐标方程为,即,
∴其参数方程为为参数).
(2)设,则到曲线的圆心的距离
,
∵,∴当时,.
∴.
选修4-5:不等式选讲
23.已知函数.
(1)若不等式的解集,求实数的值.
(2)在(1)的条件下,若存在实数使成立,求实数的取值范围.
解:(1)∵函数,
故不等式,即,
即,
求得.
再根据不等式的解集为.
可得,
∴实数.
(2)在(1)的条件下,,
∴存在实数使成立,即,
由于,
∴的最小值为2,
∴,
故实数的取值范围是.