2019届二轮复习（理）专题五立体几何5-2空间中的平行与垂直课件（34张）（全国通用） 34页

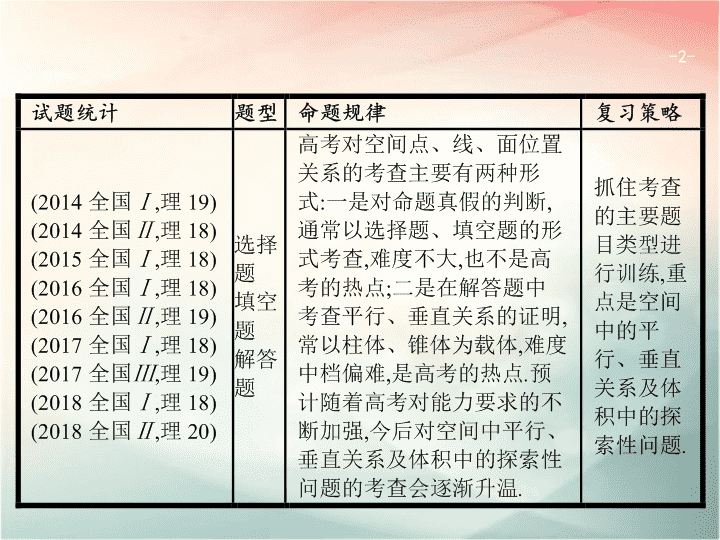
5.2 　空间中的平行与垂直 - 2 - - 3 - 命题热点一 命题热点二 命题热点三 线线、线面平行或垂直的判定与性质 【思考】 判断或证明线面、线线平行或垂直的常用方法有哪些? 例 1 (2018 全国 Ⅱ , 理 20)如图,在三棱锥 P-ABC 中, AB=BC= , PA=PB=PC=AC= 4, O 为 AC 的中点 . (1)证明: PO ⊥ 平面 ABC ; (2)若点 M 在棱 BC 上,且二面角 M-PA-C 为30 ° ,求 PC 与平面 PAM 所成角的正弦值 . - 4 - 命题热点一 命题热点二 命题热点三 - 5 - 命题热点一 命题热点二 命题热点三 - 6 - 命题热点一 命题热点二 命题热点三 - 7 - 命题热点一 命题热点二 命题热点三 题后反思 1 . 解决此类问题要注意线线平行 ( 垂直 ) 、线面平行 ( 垂直 ) 与面面平行 ( 垂直 ) 的相互转化 . 在解决线线平行、线面平行问题时 , 若题目中已出现了中点 , 可考虑在图形中再取中点 , 构成中位线进行证明 . 2 . 要证明线面平行 , 先在平面内找一条直线与已知直线平行 , 或找一个经过已知直线与已知平面相交的平面 , 找出交线 , 证明两线平行 . 3 . 要证明线线平行 , 可考虑公理 4 或转化为证明线面平行 . 4 . 要证明线面垂直可转化为证明线线垂直 , 应用线面垂直的判定定理与性质定理进行转化 . - 8 - 命题热点一 命题热点二 命题热点三 对点训练 1 如图 , 四棱锥 P-ABCD 中 , PA ⊥ 底面 ABCD , AD ∥ BC , AB=AD=AC= 3, PA=BC= 4, M 为线段 AD 上一点 , AM= 2 MD , N 为 PC 的中点 . (1) 证明 MN ∥ 平面 PAB ; (2) 求直线 AN 与平面 PMN 所成角的正弦值 . - 9 - 命题热点一 命题热点二 命题热点三 又 AD ∥ BC , 故 TN