2018-2019学年四川省遂宁市高一下学期期末考试 数学 10页

‎ 2018-2019学年四川省遂宁市高一下学期期末考试 数学 本试卷分第I卷（选择题）和第II卷（非选择题）两部分。总分150分。考试时间120分钟。‎ 第Ⅰ卷（选择题，满分60分）‎ 注意事项：‎ ‎1．答题前，考生务必将自己的姓名、班级、考号用0.5毫米的黑色墨水签字笔填写在答题卡上。并检查条形码粘贴是否正确。‎ ‎2．选择题使用2B铅笔填涂在答题卡对应题目标号的位置上，非选择题用0.5毫米黑色墨水签字笔书写在答题卡对应框内，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。‎ ‎3．考试结束后，将答题卡收回。‎ 一、选择题（本大题共12小题，每题5分，共60分。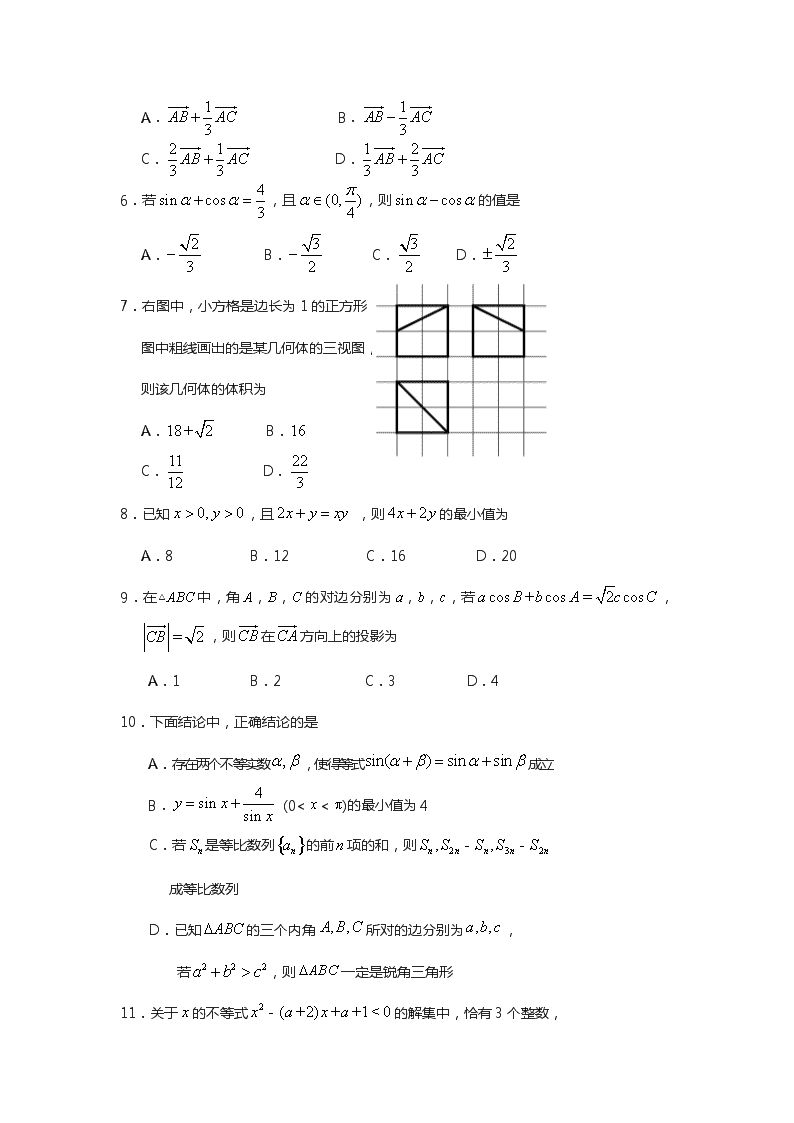在每小题给出的四个选项中，只有一项是符合题目要求）‎ ‎1．设，且，则下列各不等式中恒成立的是 A． B． C． D．‎ ‎2．已知各项均为正数的等比数列，若，则的值为 A．-4 B．4 C． D．0‎ ‎3．已知，，则 ‎ A． B． C． D．‎ ‎4．已知内角的对边分别为，满足 且，则△ABC ‎ A．一定是等腰非等边三角形 ‎ B．一定是等边三角形 ‎ C．一定是直角三角形 ‎ D．可能是锐角三角形，也可能是钝角三角形 ‎5．在中，是上一点，且，则 ‎ A． B． ‎ C． D．‎ ‎6．若，且，则的值是 A． B． C． D．‎ ‎7．右图中，小方格是边长为1的正方形，‎ 图中粗线画出的是某几何体的三视图，‎ 则该几何体的体积为 A． B． ‎ C． D．‎ ‎8．已知，且 ，则的最小值为 ‎ A．8 B．12 C．16 D．20‎ ‎9．在△ABC中，角A，B，C的对边分别为a，b，c，若，，则在方向上的投影为 ‎ A．1 B．2 C．3 D．4‎ ‎10．下面结论中，正确结论的是 A．存在两个不等实数，使得等式成立 B． (0< x < π)的最小值为4‎ C．若是等比数列的前项的和，则 ‎ 成等比数列 D．已知的三个内角所对的边分别为，‎ 若，则一定是锐角三角形 ‎11．关于的不等式的解集中，恰有3个整数，‎ 则的取值范围是 A． B． ‎ C． D． ‎ ‎12．已知数列的前项和为，‎ 令，记数列的前项为 ，则 ‎ A． B． C． D．‎ 第Ⅱ卷（非选择题，满分90分）‎ 注意事项：‎ ‎1．请用蓝黑钢笔或圆珠笔在第Ⅱ卷答题卡上作答，不能答在此试卷上。‎ ‎2．试卷中横线及框内注有“▲”的地方，是需要你在第Ⅱ卷答题卡上作答。‎ 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13．已知向量，若，则 ▲ ‎ ‎14．计算：= ▲ ‎ ‎15．已知等差数列的前项和为，若，则=‎ ‎ ▲ ‎ ‎16．一湖中有不在同一直线的三个小岛A、B、C，前期为开发旅游资源在A、B、C三岛之间已经建有索道供游客观赏，经测量可知AB两岛之间距离为3公里，BC两岛之间距离为5公里，AC两岛之间距离为7公里,现调查后发现，游客对在同一圆周上三岛A、B、C且位于（优弧）一片的风景更加喜欢，但由于环保、安全等其他原因，没办法尽可能一次游览更大面积的湖面风光，现决定在上选择一个点D建立索道供游客游览，经研究论证为使得游览面积最大，只需使得△ADC面积最大即可.则当△ADC 面积最大时建立索道AD的长为 ▲ 公里.（注：索道两端之间的长度视为线段）‎ 三、解答题：解答应写出必要的文字说明、证明过程或演算步骤.‎ ‎17．（本小题满分10分）‎ 已知向量且，‎ ‎（Ⅰ）求向量与的夹角；‎ ‎（Ⅱ）求的值. ‎ ‎▲‎ ‎18．（本小题满分12分）‎ 已知等比数列的公比，且的等差中项为10， ．‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）设， 求数列的前项和.‎ ‎▲‎ ‎19．（本小题满分12分）‎ 已知 ‎（Ⅰ）求的值；‎ ‎（Ⅱ）若，求的值。‎ ‎▲‎ ‎20.（本小题满分12分）‎ 已知在直角三角形ABC中,，（如右图所示）‎ ‎（Ⅰ）若以AC为轴，直角三角形ABC旋转一周，试说明所得几何体的结构特征并求所得几何体的表面积。‎ ‎（Ⅱ）一只蚂蚁在问题（Ⅰ）形成的几何体上从点B绕着几何体的侧面爬行一周回到点B，求蚂蚁爬行的最短距离。‎ ‎▲‎ ‎21.（本小题满分12分）‎ 已知△ABC内角A，B，C的对边分别是a，b，c，且．‎ ‎（Ⅰ）求A；‎ ‎（Ⅱ）若，求△ABC面积的最大值．‎ ‎▲‎ ‎22.（本小题满分12分）‎ 已知数列的前项和为，满足且，数列的前项为，满足 ‎（Ⅰ）设，求证：数列为等比数列；‎ ‎（Ⅱ）求的通项公式；‎ ‎（Ⅲ）若对任意的恒成立，求实数的最大值.‎ ‎▲‎ 遂宁市高中2021届第二学期期末教学水平监测 数学试题参考答案及评分意见 一、选择题（5′×12=60′）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 D B A B C A D C A A C B 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13． 14． 15． 16． 7 ‎ 三、解答题 ‎17．（本小题满分10分）‎ 解：（Ⅰ）由得 …………2分 因 ‎…………4分 向量与的夹角为 …………6分 ‎（Ⅱ）‎ ‎…………10分 ‎18．（本小题满分12分）‎ 解析：（Ⅰ）由题意可得：， ‎ ‎ ∴ …………4分 ‎∵，∴，∴数列的通项公式为．…………6分 ‎（Ⅱ） ， ∴‎ ‎ …………8分 上述两式相减 可得 ‎ ‎∴= …………12分 ‎19．（本小题满分12分）‎ 解：（I） ①‎ ‎ ② …………2分 由①+②得 ③‎ 由①-②得 ④ …………4分 ‎ 由③÷④得 …………6分 ‎（II）∵，‎ ‎，‎ ‎ …………8分 ‎…………10分 ‎ ‎ ‎…………12分 ‎ ‎20．（本小题满分12分）‎ 解：（Ⅰ）在直角三角形ABC中，由 即，得,若以AC为轴旋转一周，‎ 形成的几何体为以为半径，高的圆锥， …………3分 则,其表面积为 ‎ …………6分 ‎（Ⅱ）由问题（Ⅰ）的圆锥，要使蚂蚁爬行的最短 距离，则沿点B的母线把圆锥侧面展开为平面图形（如 右图）最短距离就是点B到点的距离, ……8分 ‎, …………10分 在中，由余弦定理得： ……12分 ‎21．（本小题满分12分）‎ 解：（I）因为，‎ 由正弦定理可得：， …………1分 所以 所以，‎ 即 ， …………3分 ‎，所以，‎ 可得： …………4分 ‎，所以，‎ 所以，可得：． …………6分 ‎（II）方法1：由余弦定理得：，……8分 得， 所以 …………9分 当且仅当时取等号， …………11分 ‎ ‎ 所以△ABC面积的最大值为 …………12分 方法2：因为，‎ 所以，， …………7分 所以，‎ ‎…………9分 所以， …………11分 当且仅当，即，当时取等号. ‎ 所以△ABC面积的最大值为 …………12分 ‎22．（本小题满分12分）‎ 解：（Ⅰ）由得，变形为：，‎ ‎…………2分 ‎ ‎，且 ‎ ‎∴数列是以首项为2，公比为的等比数列 …………4分 ‎（Ⅱ）由 …………5分 ‎ ； …………7分 ‎（Ⅲ）由（Ⅰ）知数列是以首项为2，公比为的等比数列 ‎∴，于是 ‎∴=,由得 从而 ， ∴ …………9分 当n为偶数时，恒成立，而，∴1 ………10分 当n为奇数时，恒成立，而，∴ ……11分 综上所述，，即的最大值为 …………12分