- 120.50 KB
- 2021-04-25 发布
专题一 第5讲 导数及其应用
课时训练提能
[限时45分钟,满分75分]
一、选择题(每小题4分,共24分)
1.已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(1)+ln x,则f′(1)=
A.-e B.-1
C.1 D.e
解析 f′(x)=2f′(1)+,令x=1,得f′(1)=2f′(1)+1,
∴f′(1)=-1.故选B.
答案 B
2.(2012·泉州模拟)已知曲线y=-3ln x的一条切线的斜率为,则切点的横坐标为
A.3 B.2
C.1 D.
解析 设切点为(x0,y0).
∵y′=x-,
∴x0-=,
解得x0=3(x0=-2舍去).
答案 A
3.(2012·聊城模拟)求曲线y=x2与y=x所围成图形的面积,其中正确的是
A.S=(x2-x)dx B.S=(x-x2)dx
C.S=(y2-y)dy D.S=(y-)dy
解析 两函数图象的交点坐标是(0,1),(1,1),
故积分上限是1,下限是0,
由于在[0,1]上,x≥x2,故求曲线y=x2与y=x所围成图形的面S=(x-x2)dx.
答案 B
4.函数f(x)=在[-2,2]上的最大值为2,则a的取值范围是
A. B.
C.(-∞,0] D.
解析 当x≤0时,f′(x)=6x2+6x,函数的极大值点是x=-1,极小值点是x=0,当x=-1时,f(x)=2,故只要在(0,2]上eax≤2即可,即ax≤ln 2在(0,2]上恒成立,即a≤在(0,2]上恒成立,故a≤ln 2.
答案 D
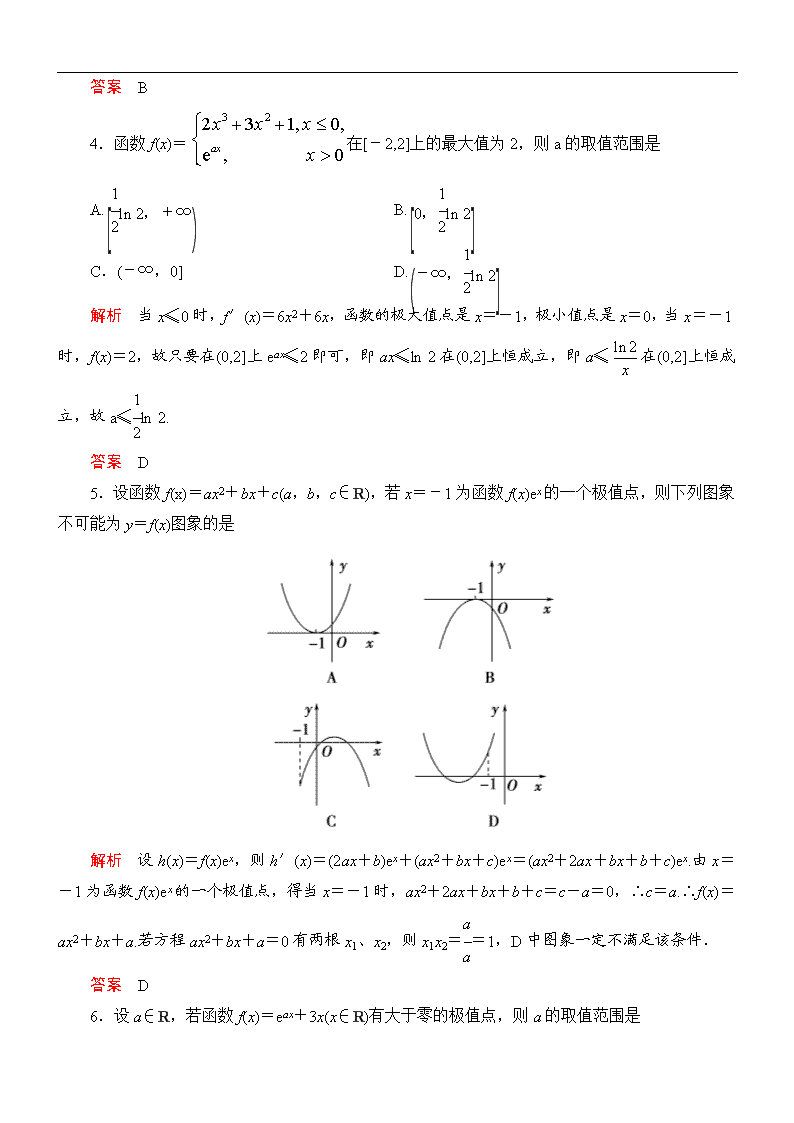
5.设函数f(x)=ax2+bx+c(a,b,c∈R),若x=-1为函数f(x)ex的一个极值点,则下列图象不可能为y=f(x)图象的是
解析 设h(x)=f(x)ex,则h′(x)=(2ax+b)ex+(ax2+bx+c)ex=(ax2+2ax+bx+b+c)ex.由x=-1为函数f(x)ex的一个极值点,得当x=-1时,ax2+2ax+bx+b+c=c-a=0,∴c=a.∴f(x)=ax2+bx+a.若方程ax2+bx+a=0有两根x1、x2,则x1x2==1,D中图象一定不满足该条件.
答案 D
6.设a∈R,若函数f(x)=eax+3x(x∈R)有大于零的极值点,则a的取值范围是
A.(-3,2) B.(3,+∞)
C.(-∞,-3) D.(-3,4)
解析 由已知得f′(x)=3+aeax,若函数f(x)在x∈R上有大于零的极值点,则f′(x)=3+aeax=0有正根.当3+aeax=0成立时,显然有a<0,此时x=ln,由x>0得到参数a的取值范围为a<-3.
答案 C
二、填空题(每小题5分,共15分)
7.(2012·济南三模)曲线y=ex+x2在点(0,1)处的切线方程为________.
解析 y′=ex+2x,∴所求切线的斜率为e0+2×0=1,
∴切线方程为y-1=1×(x-0),即x-y+1=0.
答案 x-y+1=0
8.(2012·枣庄市高三一模)dx=________.
解析 dx表示圆x2+y2=4中阴影部分的面积的大小,易知∠AOB=,OC=1,
∴dx=S△OBC+S扇形AOB
=×1×+××22=+.
答案 +
9.(2012·泉州模拟)若函数f(x)=x-a+ln x(a为常数)在定义域上是增函数,则实数a的取值范围是________.
解析 ∵f(x)=x-a+ln x在(0,+∞)上是增函数,
∴f′(x)=1-≥0在(0,+∞)上恒成立,即a≤2+.
而2+≥2=4,
当且仅当=,
即x=1时等号成立,∴a≤4.
答案 (-∞,4]
三、解答题(每小题12分,共36分)
10.(2012·泉州模拟)已知函数f(x)=x3+ax2+bx+a2(a,b∈R).
(1)若函数f(x)在x=1处有极值为10,求b的值;
(2)若对任意a∈[-4,+∞),f(x)在x∈[0,2]上单调递增,求b的最小值.
解析 (1)f′(x)=3x2+2ax+b,
则⇒或.
当时,f′(x)=3x2+8x-11,
Δ=64+132>0,所以函数有极值点;
当时,f′(x)=3(x-1)2≥0,所以函数无极值点.
则b的值为-11.
(2)解法一 f′(x)=3x2+2ax+b≥0对任意的a∈[-4,+∞),x∈[0,2]都成立,
则F(a)=2xa+3x2+b≥0对任意的a∈[-4,+∞),x∈[0,2]都成立.
∵x≥0,F(a)在a∈[-4,+∞)单调递增或为常数函数,
所以得F(a)min=F(-4)=-8x+3x2+b≥0对任意的x∈[0,2]恒成立,即b≥(-3x2+8x)max,
又-3x2+8x=-32+≤,
当x=时,(-3x2+8x)max=,得b≥,
所以b的最小值为.
解法二 f′(x)=3x2+2ax+b≥0对任意的a∈[-4,+∞),x∈[0,2]都成立,
即b≥-3x2-2ax对任意的a∈[-4,+∞),x∈[0,2]都成立,即b≥(-3x2-2ax)max,
令F(x)=-3x2-2ax=-32+.
①当a≥0时,F(x)max=0,∴b≥0;
②当-4≤a<0时,F(x)max=,∴b≥.
又∵max=,∴b≥.
综上,b的最小值为.
11.已知函数f(x)=exln x.
(1)求函数f(x)的单调区间;
(2)设x>0,求证:f(x+1)>e2x-1;
(3)设n∈N+,求证:ln(1×2+1)+ln(2×3+1)+…+ln[n(n+1)+1]>2n-3.
解析 (1)由题知,函数f(x)的定义域为(0,+∞),
由f′(x)=exln x(ln x+1).
令f′(x)>0,解得x>;
令f′(x)<0,解得0<x<.
故f(x)的增区间为,减区间为.
(2)证明 要证f(x+1)>e2x-1,即证(x+1)ln(x+1)>2x-1⇔ln(x+1)>⇔ln(x+1)->0.
令g(x)=ln(x+1)-,
则g′(x)=-=,
令g′(x)=0,得x=2,
且g(x)在(0,2)上单调递减,
在(2,+∞)上单调递增,
所以g(x)min=g(2)=ln 3-1,
故当x>0时,有g(x)≥g(2)=ln 3-1>0,
即f(x+1)>e2x-1得证.
(3)证明 由(2)得ln(x+1)>,
即ln(x+1)>2-,
所以ln[k(k+1)+1]>2->2-,
所以ln(1×2+1)+ln(2×3+1)+…+ln[n(n+1)+1]
>++…+=2n-3+>2n-3.
12.设函数f(x)=-a+x+a,x∈(0,1],a∈R*
(1)若f(x)在(0,1]上是增函数,求a的取值范围;
(2)求f(x)在(0,1]上的最大值.
解析 (1)当x∈(0,1]时,f′(x)=-a·+1.
要使f(x)在x∈(0,1]上是增函数,
需使f′(x)=-+1≥0在(0,1]上恒成立.
即a≤= 在(0,1]上恒成立.
而 在(0,1]上的最小值为,
又a∈R*,∴0<a≤为所求.
(2)由(1)知:
①当0<a≤时,f(x)在(0,1]上是增函数.
∴[f(x)]max=f(1)=(1-)a+1;
②当a>时,令f′(x)=0,得x= ∈(0,1].
∵0<x< 时,f′(x)>0;
∵ <x≤1时,f′(x)<0.
∴[f(x)]max=f=a-.
综上,当0<a≤时,[f(x)]max=(1-)a+1;
当a>时,[f(x)]max=a-.