福建省宁德市2020届高三上学期第一次质量检查（期末考试）数学理试题 24页

‎2020届宁德市普通高中毕业班第一次质量检查试卷 理 科 数 学 本试卷分第I卷和第II卷两部分．第I卷1至3页，第II卷3至5页，满分150．‎ 考生注意：‎ ‎1．答题前，考生务必将自己的准考号、姓名填写在答题卡上．考生要认真核对答题卡上粘贴的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致．‎ ‎2．第I卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．第II卷用0．5毫米的黑色墨水签字笔在答题卡上书写作答．若在试题卷上作答，答案无效．‎ ‎3．考试结束，监考员将试题卷和答题卡一并交回 ．‎ 第I卷 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1.若复数，其中是虚数单位，则复数的模为（ ）‎ A. B. C. D. 2‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 利用复数的四则运算将复数化简为a+bi的形式，然后利用复数模的公式计算即可．‎ ‎【详解】复数＝2i+＝2i+1﹣i＝1+i,‎ 则|z|＝．‎ 故选C．‎ ‎【点睛】本题考查复数的乘除运算，复数的模的求法，属于基础题．‎ ‎2.设集合，，则=( )‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 对集合分别进行不等式求解，并进行化简，再求交集，即可得答案.‎ ‎【详解】因为，‎ 集合或，‎ 所以.‎ 故选：A.‎ ‎【点睛】本题考查不等式的求解及集合的交运算，考查基本运算求解能力.‎ ‎3.已知等比数列满足，，则( )‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 利用等比数列的通项公式，将等式化成关于的方程，进而求得的值.‎ ‎【详解】因为，所以，‎ 解得：，所以.‎ 故选：A.‎ ‎【点睛】本题考查等比数列的通项公式应用，考查基本运算求解能力.‎ ‎4.若满足，则的最大值为（）‎ A. 2 B. 5 C. 6 D. 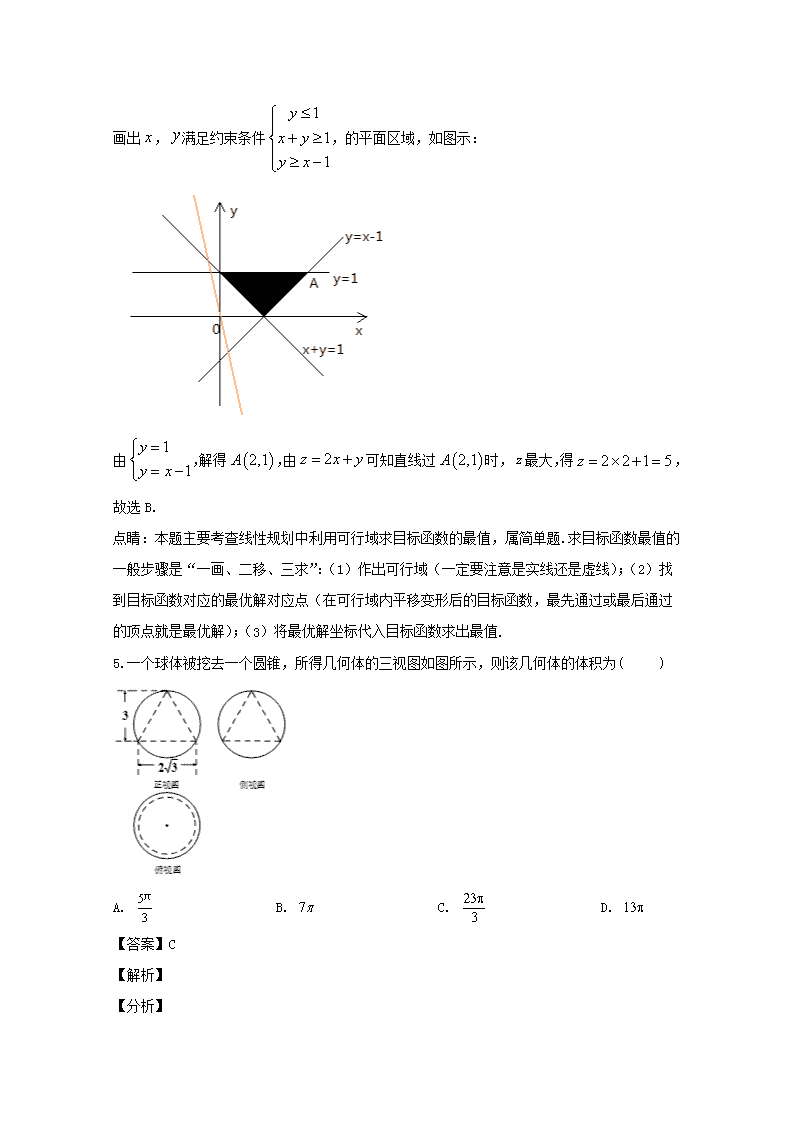7‎ ‎【答案】B ‎【解析】‎ 画出，满足约束条件，的平面区域，如图示：‎ 由，解得，由可知直线过时，最大，得，故选B.‎ 点睛：本题主要考查线性规划中利用可行域求目标函数的最值，属简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.‎ ‎5.一个球体被挖去一个圆锥，所得几何体的三视图如图所示，则该几何体的体积为( ) ‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据三视图的数据，求出球的体积后再减去圆锥的体积，即可得答案.‎ ‎【详解】如图所示，连接交于，设球的半径为，‎ 因为，所以，‎ 所以，‎ 所以.‎ 故选：C.‎ ‎【点睛】本题考查三视图还原几何体的直观图、组合体体积计算，考查空间想象能力和运算求解能力.‎ ‎6.明朝数学家程大位著的《算法统宗》里有一道著名的题目： “一百馒头一百僧，大僧三个更无争，小僧三人分一个，大、小和尚各几丁？”下图所示的程序框图反映了此题的一个算法．执行下图的程序框图，则输出的 ( )‎ A. 25 B. 45 C. 60 D. 75‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据程序框图，解方程得，即可得到答案.‎ ‎【详解】根据程序框图，当时，解得，‎ 此时，终止循环.‎ 故选：D.‎ ‎【点睛】本题考查程序框图语言和数学文化的交会，考查阅读理解能力，求解时注意将问题转化为解方程问题.‎ ‎7.若、为空间两条不同的直线，、为空间两个不同的平面，则的一个充分条件是（　　）‎ A. 且 B. 且 C. 且 D. 且 ‎【答案】D ‎【解析】‎ 考点：平面的基本性质及推论；必要条件、充分条件与充要条件的判断．‎ 专题：计算题．‎ 分析：若a⊥β且α∥β，则有a⊥α，反之不成立，于是，“a⊥β且α∥β”是“a⊥α”成立的充分不必要条件．‎ 解答：解：若a⊥β且α∥β，则有a⊥α，‎ 反之不成立，‎ 于是，“a⊥β且α∥β”是“a⊥α”成立的充分不必要条件，‎ 故选D．‎ 点评：本题考查平面的基本性质和推论，是基础题．解题时要认真审题，仔细解答．‎ ‎8.若实数，，满足，则，，的大小关系是( )‎ A. << B. <<‎ C. << D. <<‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 令，再利用对数函数与指数函数的图象，可得答案.‎ ‎【详解】令，则，‎ 因为，由的图象可得：，所以；‎ 因为与互为反函数，图象关于对称，‎ 因为，所以，‎ 综上所述：.‎ 故选：C.‎ ‎【点睛】本题考查利用函数的图象研究数的大小，考查数形结合思想、转化与化归思想，考查运算求解能力，求解时注意借助函数的图象进行研究.‎ ‎9.已知点和点关于直线对称，斜率为的直线过点交于点，若的面积为2，则的值为( )‎ A. 或 B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 先求出点的坐标，再利用的面积为2，得到关于的方程，从而求得答案.‎ ‎【详解】设点，则解得：，则，‎ 设直线的方程为：与方程联立，‎ 解得：，则，‎ 因为直线的方程为：，且，‎ 点到直线的距离，‎ 所以.‎ 故选：B.‎ ‎【点睛】本题考查点关于直线对称、点到直线距离、三角形面积公式，考查数形结合思想运用，考查运算求解能力.‎ ‎10.已知斜率为的直线过抛物线的焦点，与抛物线交于，两点，又直线与圆交于，两点．若，则的值为( )‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 利用弦长公式分别计算、关于的表达式，再利用求得的值.‎ ‎【详解】设直线的方程为代入抛物线消去，‎ 整理得：，则，‎ 所以，‎ 圆，‎ 圆心为，半径为，‎ 因为直线过圆心，所以，‎ 因为，所以.‎ 故选：A.‎ ‎【点睛】本题考查直线与圆、直线与抛物线的位置关系、弦长计算，考查转化与化归思想的应用，考查运算求解能力，求解时注意弦的特殊性，即可简化运算.‎ ‎11.已知函数的周期为，,分别是函数的图像与轴相邻的两个交点，点在函数的图像上，且满足，则的值为( )‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据题意，可令，点为坐标原点，再利用得到点的坐标，代入函数解析式，并求得的值.‎ ‎【详解】因为函数的周期为，‎ 所以，令得，‎ 令，则，‎ 因为，所以在方向的投影为，‎ 所以，所以，‎ 所以.‎ 故选：C.‎ ‎【点睛】本题考查平面向量数量积与三角函数图象的交会、三角函数的周期及对称性，考查数形结合思想，考查运算求解能力，求解过程利用特值法，令，，能使运算过程更简便.‎ ‎12.已知函数，以下四个命题：‎ ‎①当时，函数存在零点； ‎ ‎②当时，函数没有极值点；‎ ‎③当时，函数在上单调递增； ‎ ‎④当时，在上恒成立．‎ 其中的真命题为( )‎ A. ②③ B. ①④ C. ①② D. ③④‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 对函数求导得导数大于0在恒成立，可得③正确，从而排除B，C，再根据导数方程，可得当时，方程有解，故排除A，从而得到正确选项.‎ ‎【详解】因为，‎ 对③，当时，，因为时，恒成立，所以函数在上单调递增，故③正确，故排除B，C；‎ 对②，因为，令，因为，所以函数在单调递减，且时，；时，；又因为在存在是连续的函数，且，所以两个函数一定有交点，所以存在，使得，即有解，且在的两侧导数值异号，所以时，函数没有极值点是错误，故排除A.‎ 故选：D ‎【点睛】本题查利用导数研究函数的性质，考查数形结合思想、函数与方程思想，求解时要注意利用排除法进行求解，可使问题的求解更高效.‎ 第II卷 注意事项：‎ 用0.5毫米黑色签字笔在答题卡上书写作答．在试题卷上作答，答案无效．‎ 本卷包括必考题和选考题两部分．第13～21题为必考题，每个试题考生都必须做答．‎ 第22、23题为选考题，考生根据要求做答．‎ 二、填空题：本大题共4小题，每小题5分．‎ ‎13.已知向量，，若，则=_______．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 利用向量平行的坐标运算求得的值，再利用向量的坐标求数量积.‎ ‎【详解】因为，所以，‎ 所以，，所以.‎ 故答案为：.‎ ‎【点睛】本题考查向量平行与数量积坐标运算，考查基本概念的理解，属于基础题.‎ ‎14.已知定义在R上的奇函数满足，且则=_______．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 利用定义在R上的奇函数，得的值，再由得到函数的周期，从而利用函数解析式求，的值，即可得到答案.‎ ‎【详解】因为定义在R上的奇函数，所以，‎ 所以，‎ 因为，所以，‎ 所以，，‎ 所以.‎ 故答案为：.‎ ‎【点睛】本题考查奇函数的性质、函数的周期性及函数值的计算，考查函数与方程思想和运算求解能力，求解时注意的运用.‎ ‎15.若，则_______．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 由两角和的正弦展开并对等式进行化简得的值，再根据同角三角函数的基本关系，求得的值，进而利用倍角公式求得的值.‎ ‎【详解】因为，‎ 所以，整理得：，‎ 所以或 所以.‎ 故答案为：‎ ‎【点睛】本题考查两角和正弦公式、同角三角函数基本关系、倍角公式，考查三角恒等变形能力和运算求解能力.‎ ‎16.在棱长为4的正方体中，正方形所在平面内的动点到直线 ‎，的距离之差为2．设的中点为，则的最小值为_______．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 取的中点，连接，建立平面直角坐标系，求出点在正方形所在平面内的轨迹方程，再将问题转化成求的最小值.‎ ‎【详解】因为正方形所在平面内的动点到直线，的距离之差为2，‎ 则点在平面内的轨迹为双曲线，其方程为，则，‎ 取的中点，连接，则，‎ 当最小时，则最小.‎ 设，，则，，‎ 对称轴，所以函数在单调递减，‎ 所以当时，，‎ 所以的最小值为.‎ 故答案为：‎ ‎【点睛】本题以立体几何为问题背景与解析几何中的双曲线进行知识交会，考查距离的最值问题，二次函数的性质，求解时注意利用坐标法思想进行求解，考查函数与方程思想、数形结合思想，考查运算求解能力.‎ 三、解答题：本大题共6小题，满分70分．解答须写出文字说明、证明过程和演算步骤．‎ ‎17.已知各项均为正数的数列的首项，前项和为，且．‎ ‎（1）求数列的通项公式； ‎ ‎（2）设，求数列的前项和．‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）利用临差法得到，从而证明数列为等差数列，进而求得通项公式；‎ ‎（2）将通项进行改写，再利用裂项相消法进行求和.‎ 详解】（1）由两式相减，得：‎ ‎，‎ 又，，‎ 当时，且，‎ 故，得（舍去），‎ ‎，‎ 数列为等差数列，公差为，‎ 所以 ．‎ ‎（2）由（1）及题意可得，‎ 所以 ‎]‎ ‎．‎ ‎【点睛】本题考查等差数列的定义及通项公式、裂项相消法求和，考查数列中的基本量法，考查运算求解能力.‎ ‎18.如图，矩形平面，，，且，分别为，的中点．‎ ‎（1）证明：平面；‎ ‎（2）若，求二面角的大小．‎ ‎【答案】（1）证明见解析；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）取DE中点F，分别连结AF,FN，证明，再利用线面平行的判定定理证明线面平行；‎ ‎（2）以B为原点建立空间直角坐标系，得则，，，，求出为平面ABCD的一个法向量，为平面AED的法向量，从而求得二面角的大小．‎ ‎【详解】（1）证明：取DE中点F，分别连结AF,FN 又N为BC中点，‎ 所以,‎ 因为矩形ABCD中，M为AB的中点，‎ 所以 所以，‎ 所以四边形AMNF为平行四边形，‎ 所以，‎ 又因为平面,平面，‎ 所以平面．‎ ‎（2）因为矩形平面，‎ 矩形平面， ‎ 所以平面．‎ 如图，以B为原点建立空间直角坐标系，‎ 则，，，，‎ 因为轴平面ABCD，‎ 所以为平面ABCD的一个法向量，‎ 设为平面AED法向量，‎ 因为，，‎ 所以，得，‎ 故可取，‎ 则，‎ 由图可知二面角的平面角为锐角，‎ 所以二面角的大小为．‎ ‎【点睛】本题考查线面平行判定定理的运用、向量法求二面角的大小，考查空间想象能力和运算求解能力，求解时注意找到三条两两互相垂直的直线，才能建立空间直角坐标系.‎ ‎19.的内角，，的对边分别为，，，且，．‎ ‎（1）求；‎ ‎（2）若为锐角三角形，为中点，求的取值范围．‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由正弦定理，将式子中的边化成角得到，从而求得的值；‎ ‎（2）由（1）知，可得的范围，再将表示成关于的函数，从而求得的取值范围.‎ ‎【详解】（1）因为，由正弦定理，得，‎ 又，‎ 所以，‎ 所以，‎ 因为，所以，‎ 所以，又，‎ 所以.‎ ‎（2）由（1）知，‎ 根据题意得 解得. ‎ 在中，由正弦定理得，‎ 所以，‎ 因为，所以，‎ 所以.‎ 因为为中点，所以，‎ 所以，‎ 因为，所以的取值范围为.‎ ‎【点睛】本题考查正弦定理的应用、利用向量解三角形及二次函数知识应用，考查数形结合思想、函数与方程思想、转化与化归思想的综合运用，求解时要有变量思想，即将表示成关于角的函数.‎ ‎20.已知椭圆的左、右焦点分别为，，离心率为，过作直线与椭圆交于，两点，的周长为8．‎ ‎（1）求椭圆的标准方程；‎ ‎（2）问：的内切圆面积是否有最大值？若有，试求出最大值；若没有，说明理由．‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由离心率得，再利用的周长为8得，从而得到 的值，进而得到椭圆的方程；‎ ‎（2）将的内切圆面积的最大值转化为求的值最大，设，，直线，从而将面积表示成关于的函数，再利用换元法研究函数的最值.‎ ‎【详解】（1）离心率为，，‎ 的周长为8，，得，‎ ‎，，‎ 因此，椭圆的标准方程为．‎ ‎（2）设的内切圆半径为，， ‎ 又，，‎ 要使的内切圆面积最大，只需的值最大．‎ 设，，直线，‎ 联立消去得：，‎ 易得，且，，‎ 所以 ‎，‎ 设，则，‎ 设，，所以在上单调递增，‎ 所以当，即时，的最大值为3，‎ 此时，所以的内切圆面积最大为．‎ ‎【点睛】本题考查椭圆的离心率、方程的求解、焦点三角形的性质，考查转化与化归思想、函数与方程思想，考查逻辑推理能力和运算求解能力，求解时注意换元法的灵活运用.‎ ‎21.已知函数．‎ ‎（1）若，曲线在点处的切线与直线平行，求的值；‎ ‎（2）若，且函数的值域为，求的最小值．‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）对函数进行求导得，再利用导数的几何意义得，从而得到关于的方程，解方程即可得到答案；‎ ‎（2）当时，，将函数可化为，则，从而将问题转化为有解，再构造函数，利用导数研究函数的值域，从而得到的取值范围.‎ ‎【详解】（1）当时，，‎ ‎，‎ 由，‎ 得，‎ 即，‎ 解得或，‎ 当时，，此时直线恰为切线，故舍去，‎ 所以.‎ ‎（2）当时，，设，‎ 设，则，‎ 故函数可化为.‎ 由,可得 的单调递减区间为，单调递增区间为，‎ 所以的最小值为，‎ 此时，函数的的值域为 问题转化为当时，有解，‎ 即，得.‎ 设，则，‎ 故的单调递减区间为，单调递增区间为，‎ 所以的最小值为，‎ 故的最小值为．‎ ‎【点睛】本题考查导数的几何意义、利用导数研究函数的单调性、求参数的最值，考查函数与方程思想、转化与化归思想、数形结合思想，考查逻辑推理能力和运算求解能力，求解时注意对问题进行多次转化，同时注意构造函数法的应用.‎ 请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题记分．做答时请写清题号．‎ ‎22.在平面直角坐标系中，圆，以坐标原点为极点，轴正半轴为极轴，直线的极坐标方程为，直线交圆于两点，为中点.‎ ‎（1）求点轨迹的极坐标方程；‎ ‎（2）若，求的值.‎ ‎【答案】(1) ，．(2) 或．‎ ‎【解析】‎ ‎【分析】‎ ‎(1)联立极坐标方程,利用为中点与韦达定理分析求解即可.‎ ‎(2)根据极经的几何意义分别表示,再利用韦达定理求关于的方程求解即可.‎ ‎【详解】解法一：（1）圆的极坐标方程为 将代入得：‎ ‎，‎ 成立，‎ 设点对应的极径分别为，‎ 所以， ‎ 所以，‎ 所以点轨迹的极坐标方程为，．‎ ‎（2）由（1）得，‎ ‎，‎ 所以，，‎ 又，所以或，‎ 即或 解法二：‎ ‎（1）因为为中点，‎ 所以于， ‎ 故的轨迹是以为直径的圆（在的内部），‎ 其所在圆方程为：，‎ 即.‎ 从而点轨迹的极坐标方程为，． ‎ ‎（2）由（1）得，‎ ‎，‎ 令，因为，所以， ‎ 则，‎ 所以，所以，‎ 即，解得（舍去），‎ 所以，‎ 又，，‎ 所以或，‎ 即或．‎ ‎【点睛】本题主要考查了极坐标中极经的几何意义,同时根据联立方程的韦达定理方法表达出题中所给的长度,再化简求解.属于中等题型.‎ ‎23.已知在R上恒成立.‎ ‎（1）求的最大值；‎ ‎（2）若均为正数，且,求的取值范围.‎ ‎【答案】(1)2(2) ．‎ ‎【解析】‎ ‎【分析】‎ ‎(1)分,和三种情况去绝对值,将绝对值函数写成分段函数.再求最小值即可求的最大值.‎ ‎(2)由(1)得,再利用将转换为关于的表达式,再利用基本不等式求解即可.‎ ‎【详解】解：（1）构造，‎ 在上恒成立，‎ ‎，‎ 又，‎ ‎，，‎ 的最大值．‎ ‎（2）由（1）得，故．‎ ‎，‎ ‎，‎ 或．‎ 故． ‎ 当时，，‎ ‎，‎ 当且仅当，即时取“=”； ‎ 当时，，‎ ‎，‎ 当且仅当，即时取“=”． ‎ 所以的取值范围是．‎ ‎【点睛】本题主要考查了绝对值函数求解以及基本不等式的用法,属于中等题型.‎ ‎ ‎