2020九年级数学上册 第4章 相似三角形 4 5页

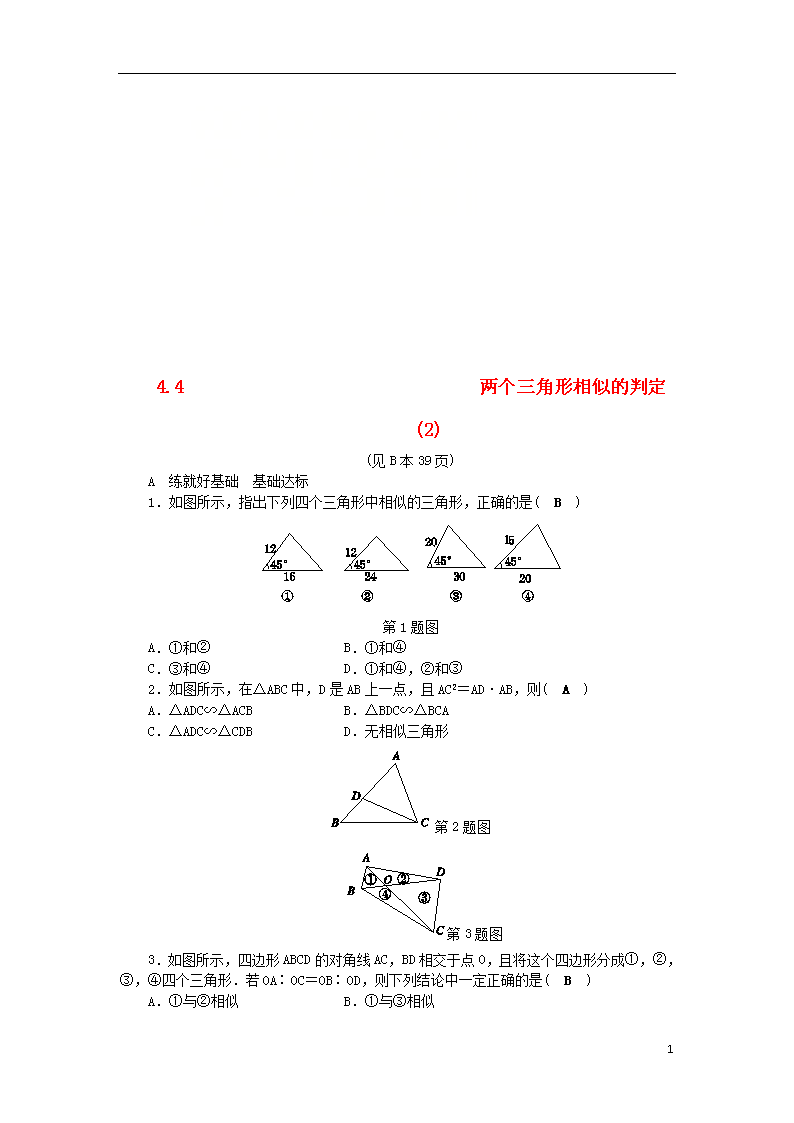
4.4 两个三角形相似的判定(2)‎ ‎(见B本39页)‎ A　练就好基础　基础达标 ‎1．如图所示，指出下列四个三角形中相似的三角形，正确的是(　B　)‎ 第1题图 A．①和② B．①和④‎ C．③和④ D．①和④，②和③‎ ‎2．如图所示，在△ABC中，D是AB上一点，且AC2＝AD·AB，则(　A　)‎ A．△ADC∽△ACB B．△BDC∽△BCA C．△ADC∽△CDB D．无相似三角形 第2题图 ‎　　第3题图 ‎3．如图所示，四边形ABCD的对角线AC，BD相交于点O，且将这个四边形分成①，②，③，④四个三角形．若OA∶OC＝OB∶OD，则下列结论中一定正确的是(　B　)‎ A．①与②相似 B．①与③相似 5‎ C．①与④相似 D．②与④相似 ‎4．如图所示，点M在BC上，点N在AM上， CM＝CN，＝，下列结论中正确的是(　B　)‎ 第4题图 A．△ABM∽△ACB B．△ANC∽△AMB C．△ANC∽△ACM D．△CMN∽△BCA ‎5．如图所示，BC平分∠ABD，AB＝9，BD＝25，当BC＝__15__时，△ABC∽△CBD.‎ 第5题图 ‎　　　　第6题图 ‎6．如图所示，零件的外径为‎25 mm，现用一个交叉卡钳(两条尺长AC和BD相等，OC＝OD)量零件的内孔直径AB.若OC∶OA＝1∶2，量得CD＝‎10 mm，则零件的厚度为__2.5__mm.‎ ‎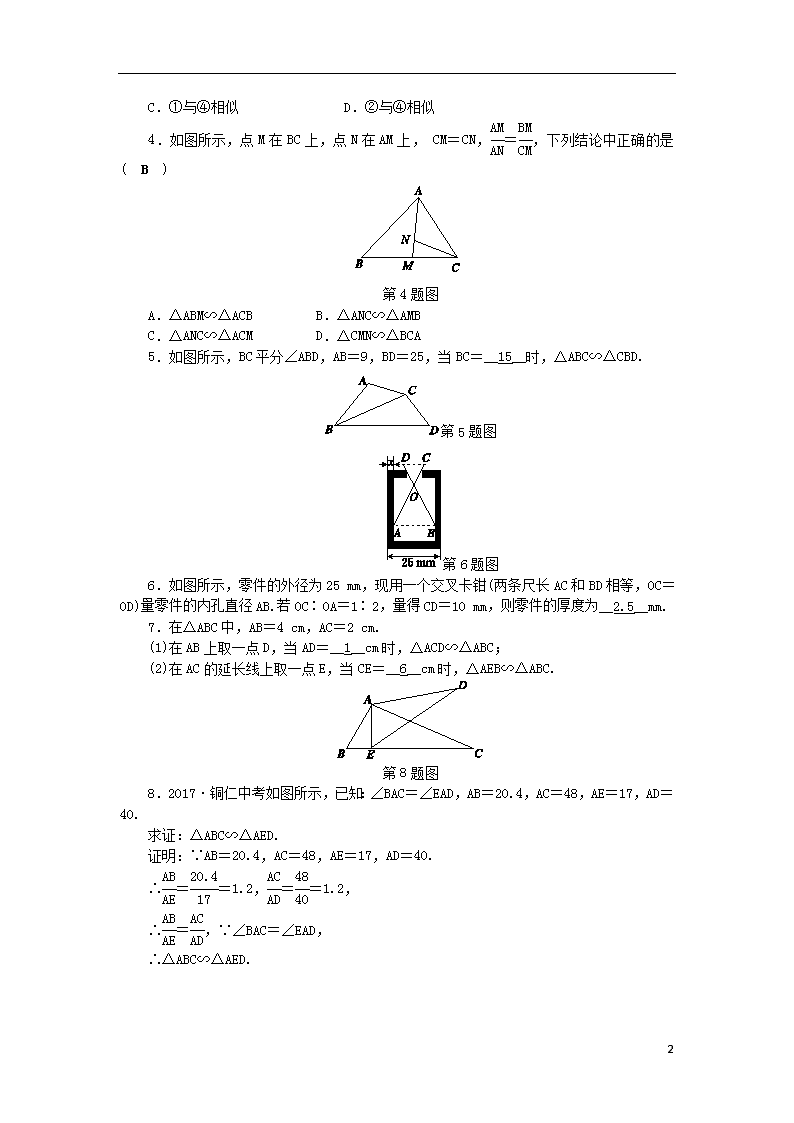7．在△ABC中，AB＝‎4 cm，AC＝‎2 cm.‎ ‎(1)在AB上取一点D，当AD＝__1__cm时，△ACD∽△ABC；‎ ‎(2)在AC的延长线上取一点E，当CE＝__6__cm时，△AEB∽△ABC.‎ 第8题图 ‎8．2017·铜仁中考如图所示，已知：∠BAC＝∠EAD，AB＝20.4，AC＝48，AE＝17，AD＝40.‎ 求证：△ABC∽△AED.‎ 证明：∵AB＝20.4，AC＝48，AE＝17，AD＝40.‎ ‎∴＝＝1.2，＝＝1.2，‎ ‎∴＝，∵∠BAC＝∠EAD，‎ ‎∴△ABC∽△AED.‎ 5‎ 第9题图 ‎9．如图所示，在△ABC中，AB＝AC，D为CB的延长线上的一点，E为BC的延长线上的一点，且满足AB2＝DB·CE.‎ 求证：△ADB∽△EAC.‎ 证明：∵AB＝AC，∴∠ABC＝∠ACB，‎ ‎∴∠ABD＝∠ACE.‎ ‎∵AB2＝DBCE，∴＝，∴＝，‎ ‎∴△ADB∽△EAC.‎ B　更上一层楼　能力提升 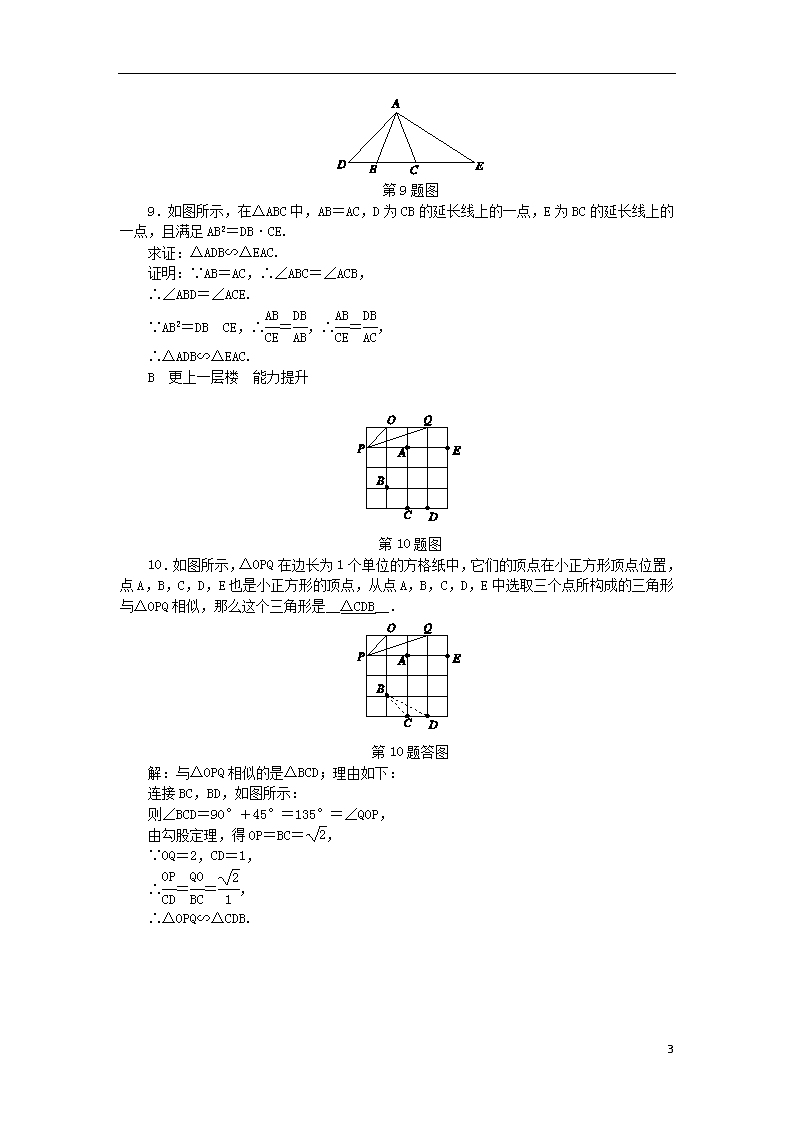第10题图 ‎10．如图所示，△OPQ在边长为1个单位的方格纸中，它们的顶点在小正方形顶点位置，点A，B，C，D，E也是小正方形的顶点，从点A，B，C，D，E中选取三个点所构成的三角形与△OPQ相似，那么这个三角形是__△CDB__．‎ 第10题答图 解：与△OPQ相似的是△BCD；理由如下：‎ 连接BC，BD，如图所示：‎ 则∠BCD＝90°＋45°＝135°＝∠QOP，‎ 由勾股定理，得OP＝BC＝，‎ ‎∵OQ＝2，CD＝1，‎ ‎∴＝＝，‎ ‎∴△OPQ∽△CDB.‎ 5‎ 第11题图 ‎11．如图所示，在△ABC中，AC＝‎8 cm，BC＝‎16 cm，点P从点A出发，沿着AC边向点C以‎1 cm/s的速度运动，点Q从点C出发，沿着CB边向点B以‎2 cm/s的速度运动，如果P与Q同时出发，经过几秒△PQC和△ABC相似？‎ 解：设经过x(s)，两三角形相似，‎ 则CP＝AC－AP＝8－x，CQ＝2x，‎ ‎①当CP与CA是对应边时，＝，即＝， 解得x＝4；‎ ‎②当CP与BC是对应边时，＝，‎ 即＝， 解得x＝.‎ 故经过4 s或 s，△PQC和△ABC相似．‎ 第12题图 ‎12．福州中考如图所示，在△ABC中，AB＝AC＝1，BC＝，在AC边上截取AD＝BC，连结BD.‎ ‎(1)通过计算，说明AD2与AC·CD的大小关系；‎ ‎(2)求∠ABD的度数．‎ 解：(1)∵AD＝BC，BC＝，‎ ‎∴AD＝，DC＝1－＝.‎ ‎∴AD2＝＝，AC·CD＝1×＝.‎ ‎∴AD2＝AC·CD.‎ ‎(2)∵AD＝BC，AD2＝AC·CD，‎ ‎∴BC2＝AC·CD，即＝.‎ 又∵∠C＝∠C，‎ ‎∴△BCD∽△ACB.‎ ‎∴＝＝1，∠DBC＝∠A.‎ 5‎ ‎∴DB＝CB＝AD.‎ ‎∴∠A＝∠ABD，∠C＝∠BDC.‎ 设∠A＝x，则∠ABD＝x，∠DBC＝x，∠C＝2x.‎ ‎∵∠A＋∠ABC＋∠C＝180°，‎ ‎∴x＋2x＋2x＝180°.‎ 解得x＝36°.∴∠ABD＝36°.‎ C　开拓新思路　拓展创新 ‎13．如图所示，在四边形ABCD中，AD∥BC.‎ 爱思考的小聪学了本节课进行了如下的推理：‎ 第13题图 ‎∵AD∥BC，‎ ‎∴△AOD∽△COB，‎ ‎∴＝，又∵∠AOB＝∠DOC，‎ ‎∴△AOB∽△DOC.‎ 你认为小聪的推理正确吗？写出你的观点．‎ 解：不正确．理由是＝与∠AOB＝∠DOC，不能构成△AOB∽△DOC的条件，因为边的对应关系错误．‎ 第14题图 ‎14．如图所示，已知△ABC，△DCE，△FEG是三个全等的等腰三角形，底边BC，CE，EG在同一直线上，且AB＝，BC＝1.连结BF，分别交AC，DC，DE于点P，Q，R.‎ ‎(1)求证：△BFG∽△FEG.‎ ‎(2)求出BF的长．‎ 解：(1)证明：∵△ABC≌△DCE≌△FEG，‎ ‎∴BC＝CE＝EG＝BG＝1，即BG＝3，‎ 又∵FE＝AB＝，∴＝＝＝，‎ 又∵∠BGF＝∠FGE，∴△BFG∽△FEG.‎ ‎(2)∵△FEG是等腰三角形，∴△BFG是等腰三角形，‎ ‎∴BF＝BG＝3.‎ 5‎