- 1.29 MB
- 2021-04-22 发布
2016—2017学年(上)期末考试
高2018级理科数学试题
考试说明:1.考试时间:120分钟
2.试题总分:150分
3.试卷页数:共4页
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个备选项中,只有一项是符合题目要求的,把答案填涂在答题卡相应位置上)
1、、均为实数,则是的( )
A.必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分也不必要条件
2、直线的倾斜角为 ( )
A. B. C. D.
3、已知抛物线过点,则它的准线方程是( )
A. B. C. D.
4、下列判断错误的是 ( )
A.“若,则方程有两个不同的实数根”是真命题.
B.命题“若,则”的逆否命题为:“若, 则”.
C.若命题:,, 则:,.
D.若为假命题,则,均为假命题.
5、已知、为不同的直线,、为不同的平面,且,,则下列命题中假命题是( )
A. 若,则 B. 若,则
C. 若,相交,则,相交 D. 若,相交,则,相交
6、已知椭圆:的左、右焦点为、,离心率为,过的直线交椭圆于、两点.若的周长为,则椭圆的方程为( )
A. B. C. D.
7、已知实数、满足,则的最大值为( )
A. B. C. D.
8、《九章算术》商功章有题:一圆柱形谷仓,高丈尺寸,容纳米斛(丈=尺,尺=寸,斛为容积单位,斛≈立方尺,≈),则圆柱底面圆的周长约为( )
A.丈尺 B.丈尺 C.丈尺 D.丈尺
9、已知椭圆的焦距为,以原点为圆心,
为半径作圆,过点作该圆的两条切线,若这两条切线互相垂直,则椭圆的离心率为( )
A. B. C. D.
10、某三棱锥的三视图如图所示,则该三棱锥的各个侧面中
最大的侧面的面积为( )
A. B.
C. D.
11、已知椭圆的方程为,是其右顶点,是该椭圆在第一象限部分上的一点,且,若点是椭圆上的动点,则的取值范围为( )
A. B. C. D.
12、已知抛物线的焦点为,准线与轴的交点为,过且倾斜角为锐角的直线与抛物线交于、两点,若,则直线的斜率为( )
A. B. C. D.
二.填空题(本大题共小题,每小题分,共分,把答案填写在答题卡相应位置上)
13、已知双曲线的一条渐近线的方程为,则 .
14、若圆:与圆:外切,则 .
15、三棱锥中,平面,,,,则三棱锥的外接球的表面积为 .
16、过曲线:的左焦点作曲线:的切线,设切点为,延长交曲线:于点,其中、有一个共同的焦点,若,则曲线的离心率为 .
三.解答题(本大题共分)
17、(本小题12分,(1)小问6分,(2)小问6分)
已知以点为圆心的圆经过点和,线段的垂直平分线交圆于点和,且.
(1) 求直线的方程; (2)求圆的方程.
18、 (本小题12分,(1)小问6分,(2)小问6分)
如图,平面,四边形为矩形,,
,点是的中点,点在边上移动.
(1)求三棱锥的体积;
(2)证明:.
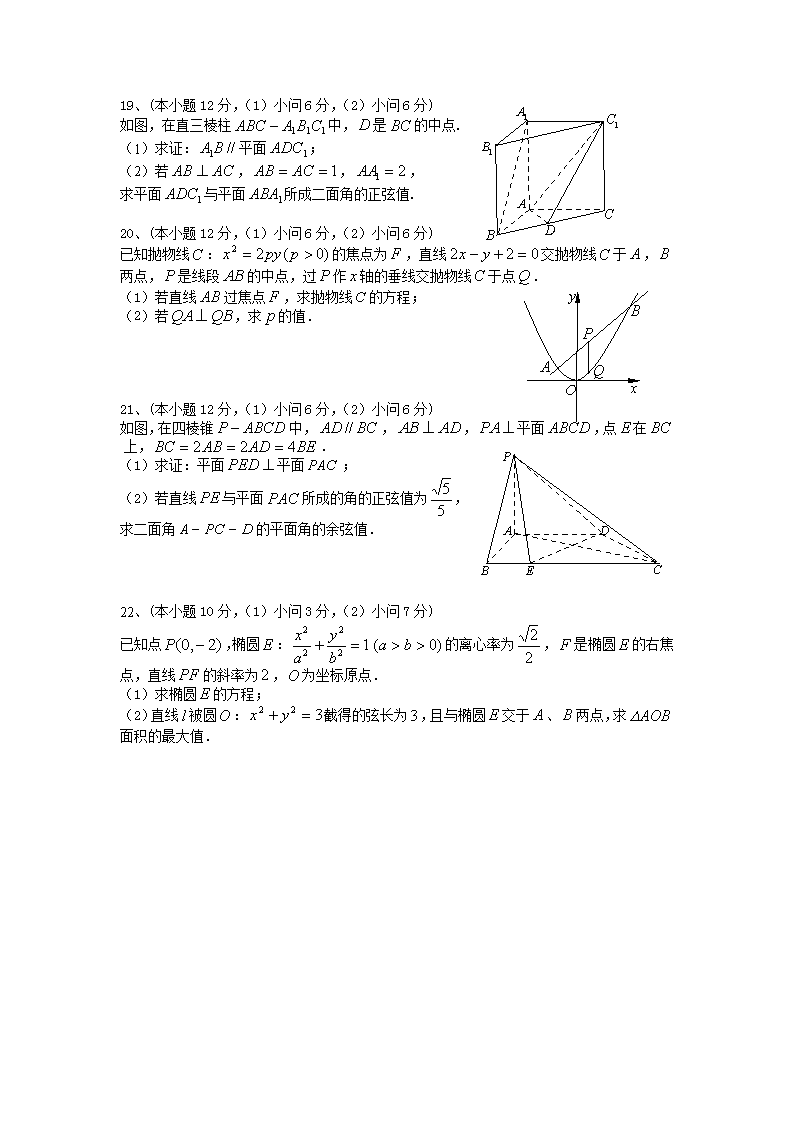
19、(本小题12分,(1)小问6分,(2)小问6分)
如图,在直三棱柱中,是的中点.
(1)求证:平面;
(2)若,,,
求平面与平面所成二面角的正弦值.
20、(本小题12分,(1)小问6分,(2)小问6分)
已知抛物线:的焦点为,直线交抛物线于,两点,是线段的中点,过作轴的垂线交抛物线于点.
(1)若直线过焦点,求抛物线的方程;
(2)若,求的值.
21、(本小题12分,(1)小问6分,(2)小问6分)
如图,在四棱锥中,,,平面,点在上,.
(1)求证:平面平面;
(2)若直线与平面所成的角的正弦值为,
求二面角的平面角的余弦值.
22、(本小题10分,(1)小问3分,(2)小问7分)
已知点,椭圆:的离心率为,是椭圆的右焦点,直线的斜率为,为坐标原点.
(1)求椭圆的方程;
(2)直线被圆:截得的弦长为,且与椭圆交于、两点,求面积的最大值.
2016—2017学年(上)期末考试
高2018级理科数学试题参考答案
一.选择题:BDADD;ACBAC;BC
12、解:易知,作轴于点,
作垂直准线于点,有,
由,可得,
所以。
二.填空题:13、3; 14、 ; 15、; 16、
16、解:设双曲线的右焦点,作抛物线的准线于点,
则易得:,,
由~,得以,∴,
∴,∴,∴。
三.解答题(本大题共分)
17、(本小题12分,(1)小问6分,(2)小问6分)
解:(1)∵直线的斜率,的中点坐标为............4分
∴直线的方程为 ............6分
(2)设圆心,则由点在上,得.①
又∵直径,∴,∴.②.........8分
由①②解得或,∴圆心或............10分
∴圆的方程为或............12分
18、 (本小题12分,(1)小问6分,(2)小问6分)
解:(1)∵平面,四边形为矩形,
∴,∴.........6分
(2)法(1)∵平面,∴,又∵且点是的中点,∴,又,,,
∴平面,...........9分
又平面,∴,由,,,
∴平面,平面,∴............12分
法(2)如图建立空间直角坐标系,
则,,,,...........8分
∴, ∵点在边上,设,
则 ,,...........10分
∴,∴............12分
19、(本小题12分,(1)小问6分,(2)小问6分)
解.(1)证明:如图,连接,交于点,则点是和的中点,连接,则,...........4分
∵平面,平面,∴平面...........6分
(2)解:如图建立空间直角坐标系,则,,,,,则,,
设平面的法向量为,则,
得,取,得,,得,...........9分
易得平面的一个法向量为,故....11分
故平面与平面所成二面角的正弦值为..........12分
20、(本小题12分,(1)小问6分,(2)小问6分)
解:(1)∵直线与轴的交点为,.....2分
∴,∴抛物线的方程为.............6分
(2)由 得:,
设,,则,,...........8分
∴,∵,则,,...........10分
,
,
代入得,解得或(舍去)
∴.................................12分
21、(本小题12分,(1)小问6分,(2)小问6分)
解:(1)法一取中点,连接,则且,
∴四边形是平行四边形,∴
∵直角△和直角△中,
∴直角△~直角△,易知,
∴ ...........2分
∵平面,平面,∴,...........4分
∵,∴平面 ,∴平面平面............6分
法二:∵平面
又∵,故可如图建立空间直角坐标系,
设,则,,,
.....2分
∴,,
∴,,∴,,∵
∴平面............4分
∴平面平面...........6分
(2)由(1),平面的一个法向量是,
设直线与平面所成的角为,
∴,∴,即......8分
设平面的一个法向量为,,
由,,∴,令,则......10分
∴ ,显然二面角的平面角是锐角,
∴二面角的平面角的余弦值为......12分
22、(本小题10分,(1)小问3分,(2)小问7分)
解:(1)设,由已知得,,得,又,得,∴,
故椭圆的方程为.......3分
(2)记点到直线的距离为,则,
①当直线与轴平行时,直线的方程为,易求,
∴.......4分
②当直线与轴不平行时,设直线的方程为,,,
由已知得,∴,......5分
由得,又,
∴,,......6分
∴,......7分
,当且仅当时取等号,......9分
综上当时,面积的最大值为.......10分
另解:……同上,
,
令,则,
当,即时,面积的最大值为,……同上.