北师大版数学九年级上册同步课件-4第四章-4 位似多边形及其性质 12页

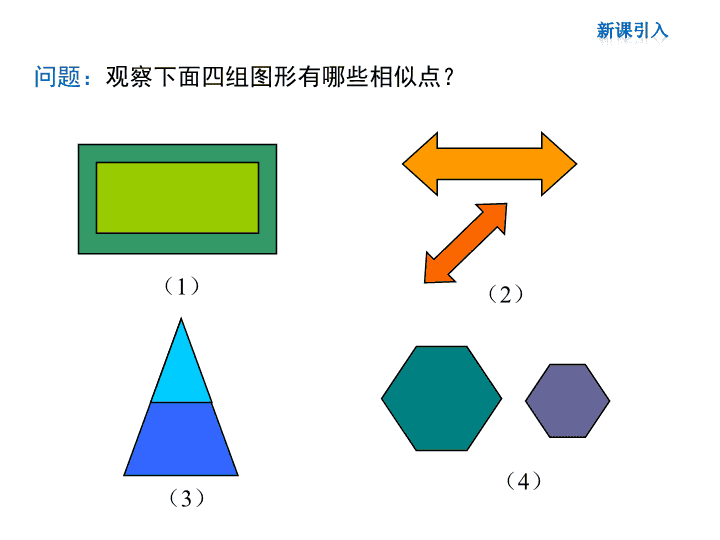
第四章 图形的相似 4.8 图形的位似 第1课时 位似多边形及其性质 学习目标 1.了解位似多边形的有关概念及位似与相似的联系与区别.（重点） 2.掌握位似图形的性质，会画位似图形.（重点） 3.会利用位似将一个图形放大或缩小.（难点） 问题：观察下面四组图形有哪些相似点？ （1） （2） （3） （4） 问题：下面两个多边形相似，将两个图形的顶点相连，观察发现 连结的直线相交于点O. 有什么关系？ A B C D E E' D' C' B' A' O .OA' OB' OC' OD' OE' OA OB OC OD OE     OE OE',OD OD',OC OC',OB OB',OA OA' 位似多边形的概念1 如果两个相似多边形任意一组对应顶点P、P̍ 所在的直线都 过同一点O,且OP ̍ =k· OP （k≠0）,那么这样的两个多边形叫做位 似多边形，点O叫做位似中心.其中k为相似多边形的相似比. 下面两组也位似多边形. A B C D E E' D' C' B' A' O 如图，已知△ABC，以点O为位似中心画△DEF，使其与 △ABC位似，且位似比为2. 解：画射线OA、OB、OC;在射线 OA、OB、OC上分别取点D、E、 F,使OD = 2OA,OE = 2OB,OF = 2OC;顺次连结D、E、F,使△DEF 与△ABC位似,相似比为2. A B C F E D O 想一想：你还有其他的画法吗？ 2 位似多边形的画法 例1 A B C 画法二：△ABC与△DEF异侧. 解：画射线OA、OB、OC;沿着射线OA、OB、 OC反方向上分别取点D、E、F,OD = 2OA,OE = 2OB,OF = 2OC;顺次连结D、E、F,使△DEF 与△ABC位似,相似比为2. O E F D 已知点O在△ABC内，以点O为位似中心画一个三角形， 使它与△ABC位似，且位似比为1:2. A B C 画法一:△ABC与△DEF在同侧. 解：画射线OA、OB、OC;在射 线OA、OB、OC上分别取点D、 E、F,使OA = 2OD,OB = 2OE,OC = 2OF;顺次连结D、E、 F,使△DEF与△ABC位似,位似 比为1：2. D E F 例2 A B C 画法二: △ABC与△DEF在异侧. 解：画射线OA、OB、OC;在射线 OA、OB、OC反向延长线上分别取 点D、E、F,使OA = 2OD,OB = 2OE, OC = 2OF;顺次连结D、E、F,使 △DEF与△ABC位似,位似比为1：2. D F E 归纳 ： 画位似图形的关键是画出图形中顶点的对应点，画图的方法大 致有两种：一是每对对应点都在位似中心的同侧；二是每对对应点在位 似中心的异侧. A B C D 1.选出下面不同于其他三组的图形（ ）B 2.已知边长为1的正方形ABCD，以它的两条对角线的交点为位似 中心，画一个边长为2且与它位似的正方形. A B C D E H GF O 解：画射线OA、OB、OC、OD;在 射线OA、OB、OC、OD上分别取 点D、E、F,使OE = 2OA , OF = 2OB , OG = 2OC , OH = 2OD;顺次 连结E、F、G、H,使正方形ABCD 与正方形EFGH位似,相位似比为1： 位似多边形 及其性质 定义 性质 如果两个相似多边形任意一组对应顶点P、 P̍ 所在的直线都过同一点O,且OP ̍ =k· OP （k≠0）,那么这样的两个多边形叫做位似多边形. 作位似图形：关键是确定位似中心、相似 比和找关键点的对应点. ① 两个图形相似. ②对应点的连线相交于一点，对应边互相 平行或在同一直线上. ③任意一对对应点到位似中心的距离之比 等于相似比. 画法