八年级下数学课件：17-1 勾股定理 （共20张PPT）1_人教新课标 20页

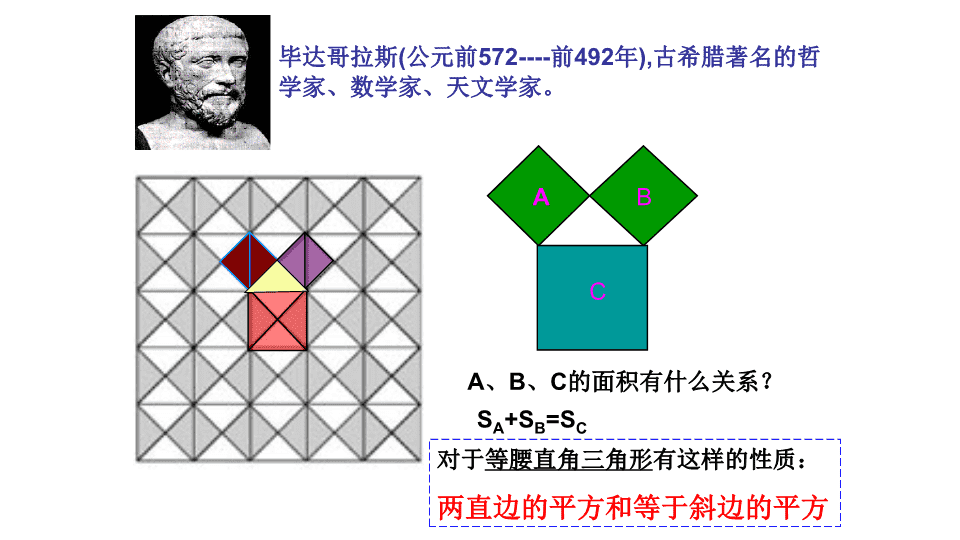
勾股定理 勾 股 弦 毕达哥拉斯(公元前572----前492年),古希腊著名的哲 学家、数学家、天文学家。 A、B、C的面积有什么关系？ SA+SB=SC A B C 对于等腰直角三角形有这样的性质： 两直边的平方和等于斜边的平方 那么对于一般的直角三角形是否也有这样的性质呢？ A B C A B C A的面 积(单位 长度) B的面 积(单位 长度) C的面 积(单位 长度) 图2 图3 A、B、 C面积 关系 直角三 角形三 边关系 图2 图3 4 9 13 9 25 34 sA+sB=sC 两直角边的平方和 等于斜边的平方 命题１：如果直角三角形的两直角边长分 别为a、b，斜边长为c，那么a2+b2=c2。 ca b c b a 用赵爽弦图证明勾股定理 = 证法一： b a 22 ba  2c 中黄实 (b- a)2 赵爽弦图的证法 化简得： c2 =a2+ b2 c b a ba b a b a c c c S大正方形 S小正方形 4S直角三角形＝ ＋ c2＝(b－a)2＋4× ab 2 1 激 励 引 导 茄菲尔德的证法 b a c b ac c c S三角形1 S三角形2 S三角形3 S梯形 化简得: c2=a2+ b2 ＝＋ ＋ (a＋b)(a＋b) 2 1ab 2 1 ab 2 1 ＋＋ c2＝ 2 1 激 励 引 导 证法二： a a b b c c 伽菲尔德证法: )ba)(ba( 2 1S 梯形 2 S c 2 1ab 2 1ab 2 1S 梯形 ∴ a2 + b2 = c2 如果直角三角形两直角边分别为a，b，斜 边为c，那么 a2 + b2 = c2 即直角三角形两直角边的平方和等于斜边的平方. 勾股定理 ca b ca b 1、如图已知：a＝3， b＝4，求c 2、如图已知： c ＝10，a＝6，求b 3、如图已知： c ＝13， a＝5，求阴影总分面积 a c a bc c2=a2 + b2 如果直角三角形两直角边分别为a，b，斜 边为c，那么 a2 + b2 = c2 勾股定理 结论变形 3.在 ABC中, ∠ C=90°, 　　　　 (1)若c=10,a:b=3:4,则a=____,b=___. (2)若a=9,b=40,则c=______. 4.在 ABC中, ∠ C=90°,若AC=6,CB=8,则ABC 面积为_____,斜边为上的高为______. 6 8 41 24 4.8 5、已知：△ABC，AB＝AC＝17， 　BC＝16，则高AD＝＿＿＿， 　S△ABC＝＿＿＿. 15 120 6、已知等边三角形ABC的边长6cm， (1)求高AD的长；(2)S△ABC A B CD 解：(1)∵△ABC是等边三角形，AD是高 在Rt△ABD中 ,根据勾股定理 222 BDABAD  cmAD 3327936  ADBCS ABC  2 1)2( )(39336 2 1 2cm 3 2 1  BCBD E D C B A 7、如图，所有的四边形都是正方形，所 有的三角形都是直角三角形，其中最大 的正方形E的边长为7cm，求正方形A，B， C，D的面积的和 精选P57 8 小明妈妈买了一部29英寸（74厘米） 的电视机.小明量了电视机的屏幕后，发现 屏幕只有58厘米长和46厘米宽，他觉得一 定是售货员搞错了.你同意他的想法吗？你 能解释这是为什么吗？ 58厘米 46厘米 74厘 米 活动五  274 5476 2 258 46 5480  ∴售货员没搞错 ∵ 荧屏对角线大约为74厘米 274 5476 直角三角形两直角边的平方和等于斜边的平方 课 堂 总 结 2 2 2a b c  a b c １、本节课我们经历了怎样的过程？ 　　经历了从实际问题引入数学问题然后发现定理，再到探 索定理，最后学会验证定理及应用定理解决实际问题的过程。 ２、本节课我们学到了什么？ 　　通过本节课的学习我们不但知道了著名的勾股定理，还 知道从特殊到一般的探索方法及借助于图形的面积来探索、 验证数学结论的数形结合思想。 ３、学了本节课后我们有什么感想？ 　　 很多的数学结论存在于平常的生活中，需要我们用数学 的眼光去观察、思考、发现，这节课我们还受到了数学文化 辉煌历史的教育。 再 见