2020届二轮复习　三角函数的图象与性质课件（全国通用） 17页

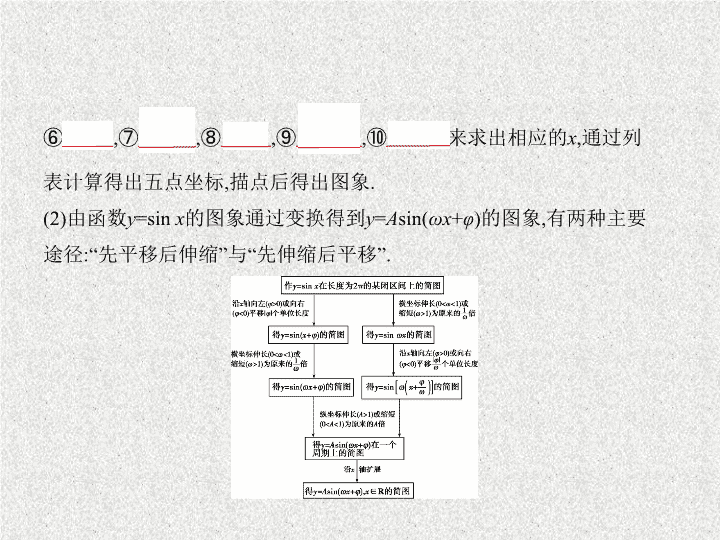
§4.2 三角函数的图象与性质 高考理数 考点一　三角函数的图象及其变换 1.“五点法”作图原理:在确定正弦函数 y =sin x 在[0,2π]上的图象 的形状时,起关键作用的五个点是① 　(0,0)     、②             、③ 　(π, 0)     、④             、⑤ 　(2π,0)     . 2.作 y = A sin( ωx + φ )( ω >0)的图象主要有以下两种方法: (1)五点法 用五点法作 y = A sin( ωx + φ )的简图,主要是通过变量代换,设 z = ωx + φ ,由 z 取 知识清单 ⑥ 　0     ,⑦             ,⑧     π     ,⑨             ,⑩ 　2π     来求出相应的 x ,通过列 表计算得出五点坐标,描点后得出图象. (2)由函数 y =sin x 的图象通过变换得到 y = A sin( ωx + φ )的图象,有两种主要 途径:“先平移后伸缩”与“先伸缩后平移”.   上述两种变换的区别:先相位变换再周期变换(伸缩变换),平移的量是| φ | 个单位;而先周期变换(伸缩变换)再相位变换,平移的量是   ( ω >0)个单 位.原因在于相位变换和周期变换都是针对 x 而言的. 3. y = A sin( ωx + φ )( A >0, ω >0), x ∈[0,+ ∞ )表示一个振动量时, A 叫做   　振 幅     , T =   叫做   　周期     , f =   =   叫做   　频率     , ωx + φ 叫做        相位     , x =0时的相位 φ 称为   　初相     . 考点二　三角函数的性质及其应用 求函数 y = A sin( ωx + φ )+ B 解析式的方法与步骤 (1)求 A 、 B ,确定函数的最大值 M 和最小值 m ,则 A =   , B =   . (2) ω 由周期得到, ω =   ,确定周期时可利用以下结论: a.函数图象的相邻两条对称轴之间的距离为函数的半个周期; b.函数图象的相邻两个对称中心间的距离也为函数的半个周期; c.一条对称轴和与其相邻的一个对称中心间的距离为函数的   个周期 (借助图象很好理解、记忆). (3)利用峰点、谷点或零点列出关于 φ 的方程,结合 φ 的范围解得 φ 的值, 所列方程如下: 根据图象确定函数解析式 方法 1 方法技巧 峰点: ωx + φ =   +2 k π;谷点: ωx + φ =-   +2 k π. 利用零点时,要区分该零点是升零点,还是降零点. 升零点(图象上升时与 x 轴的交点): ωx + φ =2 k π; 降零点(图象下降时与 x 轴的交点): ωx + φ =π+2 k π. (以上 k ∈Z) A. y =sin   　    B. y =sin   C. y =sin   　    D. y =sin   例 1    (2017 河南南阳一中四模 ,8) 函数 f ( x )= A sin( ωx + φ )   的部分图象如图所示 , 若将 f ( x ) 图象上所有点的横坐标缩短为原来的   ( 纵坐标不变 ), 得到函数 g ( x ) 的图象 , 则 g ( x ) 的解析式为   ( A 　 ) 解析　根据函数的图象知 A =1,   =   -   =   , 则 T =π, ω =   =2,利用 f   =1, 解得 φ = k π+   ( k ∈Z), 由于| φ |<   ,所以 φ =   , 求得 f ( x )=sin   ,将 f ( x )图象上所有点的横坐标缩短为原来的   (纵 坐标不变)得到 g ( x )=sin   的图象,故选A. 1.已知三角函数解析式求单调区间 (1)求函数的单调区间应遵循简单化原则,将解析式进行化简,并注意复 合函数单调性规律“同增异减”. (2)求形如 y = A sin( ωx + φ )或 y = A cos( ωx + φ )(其中 ω >0)的单调区间时,要视 “ ωx + φ ”为一个整体,通过解不等式求解.如果 ω <0,那么一定先借助诱 导公式将 ω 化为正数. 2.已知三角函数的单调区间求参数,先求出函数的单调区间,然后利用集 合间的关系求解. 三角函数的单调性问题的常见类型及解题策略 方法 2 例 2    (2015 天津 ,14,5 分 ) 已知函数 f ( x )=sin ωx +cos ωx ( ω >0), x ∈ R. 若函数 f ( x ) 在区间 (- ω , ω ) 内单调递增 , 且函数 y = f ( x ) 的图象关于直线 x = ω 对称 , 则 ω 的值为 　　　     . 解题导引 解析　由已知得 f ( x )=   sin   , 令 2 k π-   ≤ ωx +   ≤ 2 k π+   , k ∈Z, 由 ω >0, 得   ≤ x ≤   , k ∈Z, 当 k =0 时 , f ( x ) 的单调递增区间为   , 所以 (- ω , ω ) ⊆   , 所以   解得 0< ω ≤   , 又 y = f ( x ) 的图象关于直线 x = ω 对称 , 所以 ω 2 +   = k π+   , k ∈Z, 解得 ω 2 = k π+   , k ∈Z,又0< ω ≤   ,所以 ω =   . 答案       1.若 f ( x )= A sin( ωx + φ )( A , ω , φ 为常数, A ≠ 0)为偶函数,则 φ = k π+   ( k ∈Z),同 时当 x =0时, f ( x )取得最大值或最小值.若 f ( x )= A sin( ωx + φ )为奇函数,则 φ = k π( k ∈Z),同时当 x =0时, f ( x )=0. 2.求三角函数的最小正周期,一般先通过恒等变形化为 y = A sin( ωx + φ )或 y = A cos( ωx + φ )或 y = A tan( ωx + φ )( A , ω , φ 为常数, A ≠ 0)的形式,再分别应用公 式 T =   或 T =   或 T =   求解. 3.函数 f ( x )= A sin( ωx + φ )( A , ω , φ 为常数, A ≠ 0)图象的对称轴一定经过图象 的最高点或最低点,对称中心的横坐标一定是函数的零点,因此在判断 直线 x = x 0 或点( x 0 ,0)是否是函数图象的对称轴或对称中心时,可通过检验 f ( x 0 )的值进行判断. 三角函数的奇偶性、周期性、对称性的求解方法 方法 3 例3    (2017全国100所名校高考数学冲刺卷,9)若函数 f ( x )=sin   的 图象向左平移   个单位后,得到 y = g ( x )的图象,则下列说法错误的是   (　 C 　) A. y = g ( x )的最小正周期为π B. y = g ( x )的图象关于直线 x =   对称 C. y = g ( x )在   上单调递增 D. y = g ( x )的图象关于点   对称 解析　把函数 f ( x )=sin   的图象向左平移   个单位后,得到 y = g ( x )= sin   的图象,故 g ( x )的最小正周期为   =π,故A正确;令 x =   ,可得 g ( x )=1,为最大值,故 y = g ( x )的图象关于直线 x =   对称,故B正确;在   上,2 x +   ∈   ,故 y = g ( x )在   上没有单调性,故C错误;由 x =   ,可得 g ( x )=0,故 y = g ( x )的图象关于点   对称,故D正确,故选C.