- 926.00 KB
- 2021-04-16 发布
田家炳高中2018-2019学年度下学期期中考试卷
高二数学(文)
一、选择题(本大题共有12个小题,每小题只有一项是符合题意,请将答案答在答题卡上。每小题5分,共60分)
1.设全集U=R,A=,B =, 则下图中阴影部分表示的集合为( )
A. B. C. D.
2.已知集合,则 ( )
A. B. C. D.
3.为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
做不到"光盘"
能做到"光盘"
男
45
10
女
30
15
附:
.
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过1%的前提下,认为"该市居民能否做到'光盘'与性别有关"
B.在犯错误的概率不超过1%的前提下,认为"该市居民能否做到'光盘'与性别无关"
C.有90%以上的把握认为"该市居民能否做到'光盘'与性别有关"
D.有90%以上的把握认为"该市居民能否做到'光盘'与性别无关"
4.在一线性回归模型中,计算相关指数,下列哪种说法不够妥当?( )
A.该线性回归方程的拟合效果较好
B.解释变量对于预报变量变化的贡献率约为
C.随机误差对预报变量的影响约占
D.有的样本点在回归直线上
5.已知复数的共轭复数 (为虚数单位),则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.如图,在复平面内,点表示复数,则图中表示的共轭复数的点是( )
A. B. C. D.
7.若命题“,使得”是假命题,则实数的取值范围是( )
A. B. C. D.
8.定义运算,则符合条件的复数为( )
A. B. C. D.
9.复数满足,则 ( )
A. B. C. D.
10.在复平面上的中, ,.则对应的复数是( )
A. B. C. D.
11.计算 ( )
A. B. C. D.
12.已知集合,,,则实数的为( )
A. B. C. 或 D. 或
二、填空题(本大题共有4个小题。每空5分,共20分)
13.设,定义与的差集为且,则__________
14.设A、B是的子集,若则称为一个“理想配集”,那么符合此条件的“理想配集”的个数是__________(规定与是两个不同的“理想配集”).
15.观察下列各式: ,则
16.有三张卡片,分别写有1和2,1和3,2和3.甲、乙、丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是__________.
三、解答题(本大题共有6个小题,17题10分满分70分。解答应写出必要的文字说明、证明过程或演算步骤)
17.已知集合
1.若是单元素集合,求集合;
2.若中至少有一个元素,求的取值范围.
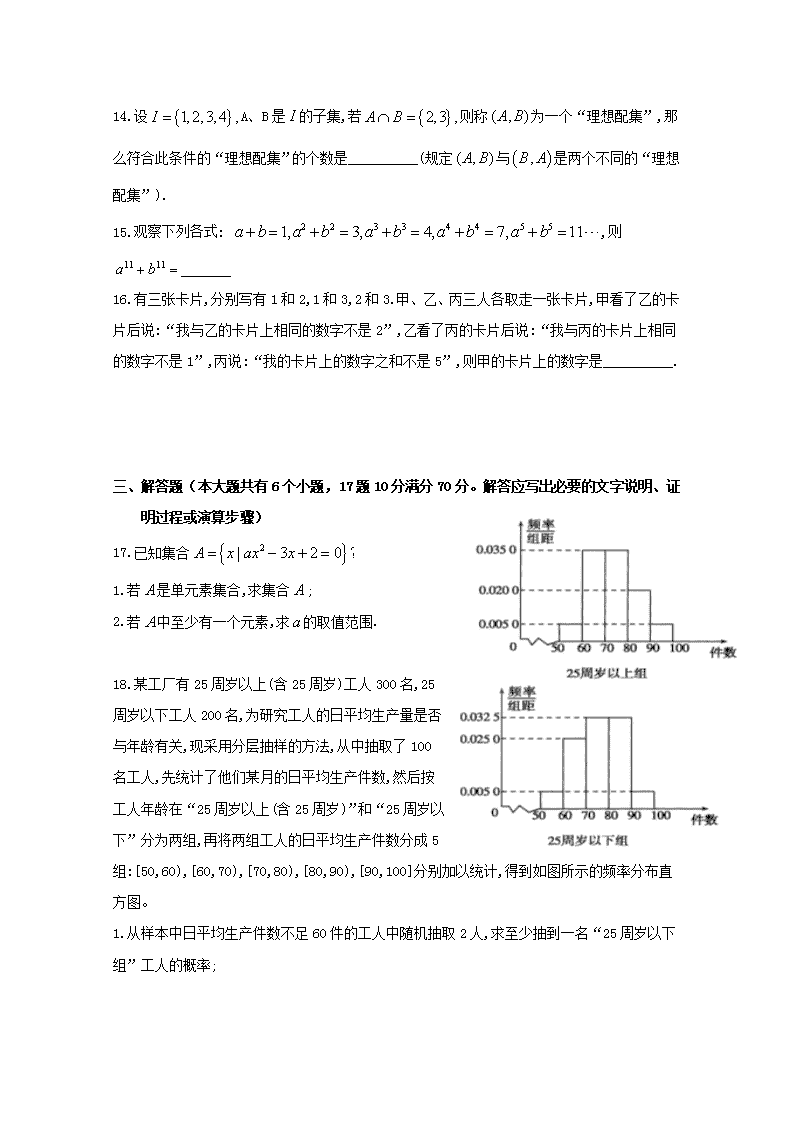
18.某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名,为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:[50,60),[60,70),[70,80),[80,90),[90,100]分别加以统计,得到如图所示的频率分布直方图。
1.从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;
2.规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
(注:)
生产能手
非生产能手
合计
25周岁以上组
25周岁以下组
合计
0.100
0.050
0.010
0.001
2.706
3.841
6.635
10.828
19.设:实数满足 (),实数满足.
1.若且“”为真,求实数的取值范围;
2.若是的必要不充分要条件,求实数的取值范围.
20.从某居民区随机抽取个家庭,获得第个家庭的月收入 (单位:千元)与月储蓄 (单位:千元)的数据资料,算得, ,,
.
1.求家庭的月储蓄对月收入的线性回归方程;
2.判断变量与之间是正相关还是负相关;
3.若该居民区某家庭月收入为千元,预测该家庭的月储蓄.
其中,为样本平均值,线性回归方程也可写为,
附:线性回归方程中, ,
21.实数为何值时,复数是:
1.实数;
2.虚数;
3.纯虚数;
4. .
22.已知复数,求复数的模的最大值、最小值.
高二文科数学期中考试答案
1.答案:B
2.答案:A
解析:或,,所以,故A
3.答案:C
解析:由题设知, ,,,,所以,
.
由附表可知,有90%以上的把握认为“该市居民能否做到‘光盘’与性别有关”,故选C
4.答案:D
解析:由相关指数的意义可知,A,B,C说法均妥当.相关指数,其值较大,说明残差平方和较小,绝大部分样本点分布在回归直线附近,不一定有的样本点在回归直线上.
5.答案:D
解析:由知,所以对应的点的坐标为,位于第四象限
6.答案:B
解析:由复数的几何意义及共轭复数定义可知,共轭复数对应的点关于轴对称(实数的共轭复数是其本身)
7.答案:A
解析:
∵命题“,使得”是假命题,∴,使得是真命题,∴,∴,∴,∴.故选A.
8.答案:A
解析:∵,
∴,
故选A
9.答案:D
解析:由,得,则,故
10.答案:B
解析:∵,且,∴,∴,故选B.
11.答案:B
解析:
12.答案:B
解析:
由题意
解得.
13.答案:
解析:因为, ,且,
所以且,且
14.答案:9
解析:对子集A分类讨论:
当A是二元集{2,3},B可以为{1,2,3,4},{2,3,4},{1,2,3},{2,3},共四种结果
A是三元集{1,2,3}时B可以取 {2,3,4},{2,3},共2种结果
A是三元集{2,3,4}时,B可以为{1,2,3},{2,3},共2种结果
当A是四元集{1,2,3,4},此时B取{2,3},有1种结果,
根据计数原理知共有4+2+2+1=9种结果,
故答案为:9.
15.199
解析:
,,,
16.答案:1和3
解析:丙说他的卡片上的数字之和不是5,所以丙的卡片上的数字要么是1和2,要么是1和3.又乙说他与丙的卡片上相同的数字不是1,所以卡片2和3必定在乙手中.因为甲与乙的卡片上相同的数字不是2,所以甲的卡片上的数字只能是1和3.
17.答案:1.因为集合是方程的解集,
则当时, ,符合题意;
当时,方程应有两个相等的实数根,则,解得,此时,符合题意.
综上所述,当时, ,当时, .
2.由1问可知,当时, 符合题意;
当时,要使方程有实数根,则,解得且.
综上所述,若集合中至少有一个元素,则.
18.答案: 1.由已知得,样本中有周岁以上组工人名, 周岁以下组工人名.
所以样本中日平均生产件数不足件的工人中, 周岁以上组工人有 (人),记为;25周岁以下组工人有 (人),记为.从中随机抽取2名工人,所有的可能结果共有种,它们是: ,,,,,,,,,.
其中,至少名“周岁以下组”工人的可能结果共有种,它们是
,,,,,,.故所求的概率.
2.由频率分布直方图可知,在抽取的名工人中,“周岁以上组”中的生产能手有
(人),“周岁以下组”中的生产能手有 (人),据此可得列联表如下:
生产能手
非生产能手
合计
25周岁以上组
15
45
60
25周岁以下组
15
25
40
合计
30
70
100
所以得.
因为,所以没有的把握认为“生产能手与工人所在的年龄组有关”.
19.答案:1.由得,
得,则.
由 解得.
即.
若,则,
若为真,则同时为真,
即,解得,
∴实数的取值范围.
2.若是的充分不必要条件,即是的充分不必要条件,
∴,即,
解得
20.答案 1.由题意知,
,,
,
,
由此可得,,
故所求线性回归方程为.
2.由于变量的值随值的增加而增加,故与之间是正相关.
3.将代入回归方程可以预测该家庭的月储蓄为 (千元).
21.答案:1.当,即或时, 是实数.
2.当,即且时, 是虚数.
3.当即时, 是纯虚数.
4.当即时, 是.
22.答案:解法一:由已知得,复数对应的点在复平面内以原点为圆心, 为半径的圆上,设,
∴.
∴.
∴复数对应的点在复平面内以为圆心, 为半径的圆上,
此时圆上的点对应的复数的模有最大值,圆上的点对应的复数的模有最小值.
如图,故,.