- 431.51 KB
- 2021-04-16 发布
第四章 三角形
解直角三角形的实际应用
中考数学复习冲刺专项训练精讲
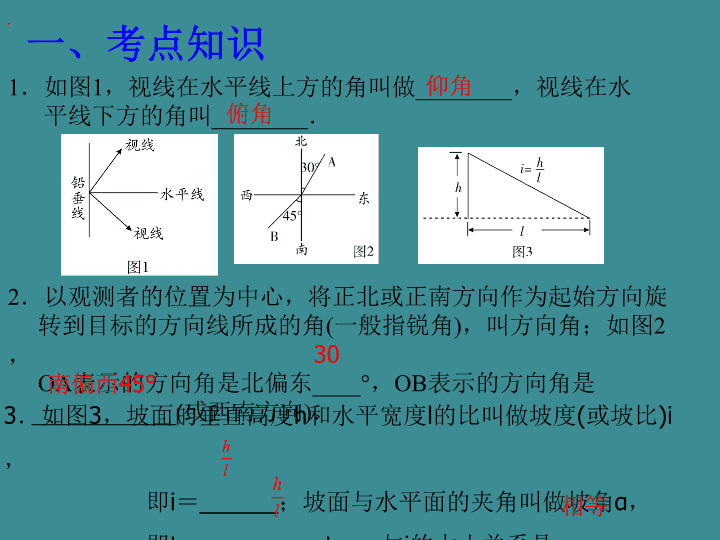
1.如图1,视线在水平线上方的角叫做________,视线在水
平线下方的角叫________.
一、考点知识,
2.以观测者的位置为中心,将正北或正南方向作为起始方向旋
转到目标的方向线所成的角(一般指锐角),叫方向角;如图2,
OA表示的方向角是北偏东____°,OB表示的方向角是
____________(或西南方向).
仰角
俯角
30
南偏西45°
3.如图3,坡面的垂直高度h和水平宽度l的比叫做坡度(或坡比)i,
即i=______;坡面与水平面的夹角叫做坡角α,
即tan α=____;tan α与i的大小关系是______.相等
h
l h
l
【变式1】如图,某幼儿园为了加强安全管理,决定
将园内的滑滑板的倾斜度由45°降为30°,已知原滑
滑板AB的长为5米,点D,B,C在同一水平地面
上.求:改善后滑滑板会加长多少米?(精确到0.1;
参考数据: ≈1.41)
解:在Rt△ABC中,∵AB=5,∠ABC=45°,
∴AC=AB·sin45°= ,
在Rt△ADC中,∠ADC=30°,AD=
∴AD-AB=7.05-5=2.05(m),
所以改善后滑滑板会加长约2.1 m.
2
2 5 25 2 2
5 2 5 1.41 7.05sin30
AC
【考点2】方向角
【例】如图,有小岛A和小岛B,轮船以45 km/h的速度由C
向东航行,在C处测得A的方向角为北偏东60°,测得B的方
向角为南偏东45°,轮船航行2小时后到达小岛B处,在B处测
得小岛A在小岛B的正北方向.求小岛A与小岛B之间的距离(结
果保留整数;参考数据: ≈2.45, ≈1.41)
解:过点C作CP⊥AB于点P,
∵∠BCF=45°,∠ACE=60°,AB∥EF,
∴∠FCB=∠PBC=45°,∠CAP=60°.
∵轮船的速度是45 km/h,轮船航行2小时,∴BC=90,
∵BC2=BP2+CP2,∴BP=CP= ,
∵∠CAP=60°,∴tan60°= ,∴AP= ,
∴AB=AP+PB= ≈15×2.45+45×1.41
≈100(km).
6 2
45 2
45 2CP
AP AP
15 6
15 6 45 2
A组
1.如图,A岛在B岛的北偏东50度方向,C岛在B岛的北偏东
80度方向,C岛在A 岛的南偏东30度方向,从C岛看A,B两
岛的视角∠ACB是多少度?
三、过关训练
2.河堤横断面如图所示,堤高BC=6米,迎水坡AB的坡比
为1∶ ,求AB的长.
解:70°
3
解:在Rt△ABC中,BC=6米, ,
∴ AC= .
∴AB= (米).
1
3
BC
AC
3 6 3BC
22 2 26 3 6 12AC BC
B组
3.如图,天星山山脚下西端A处与东端B处相距
800(1+ )米,小军和小明同时分别从A处和B处
向山顶C匀速行走.已知山的西端的坡角是45°,东
端的坡角是30°,小军的行走速度为 米/秒.若小
明与小军同时到达山顶C处,则小明的行走速度是多少?
解:过点C作CD⊥AB于点D,
设AD=x米,小明的行走速度是a米/秒,
∵∠A=45°,CD⊥AB,
∴AD=CD=x米,∴AC= .
在Rt△BCD中,∵∠B=30°,
∴BC=CD÷sin30°=2x.
∵小军的行走速度为 米/秒,小明与小军同时到达山顶C处,
∴2x÷ =2x÷a,解得a=1米/秒.
3
2
2
2x
2
2
2
2
4.如图,为测量一座山峰CF的高度,将此山的某
侧山坡划分为AB和BC两段,每一段山坡近似是“直”
的.其中测得坡长AB=800米,BC=200米,坡角
∠BAF=30°,∠CBE=45°.求山峰的高度CF.(结果
取整数;参考数据: ≈1.414)
解:过B作BG⊥AF于点G,则BG=EF,BE=GF,
在Rt△ABG中,∵AB=800,∠BAF =30°,
∴EF=BG=ABsin∠BAF =800× =400(米),
在Rt△BCE中,∵BC=200(米),∠CBE=45°,
∴CE=BCsin∠CBE=200× = ≈141.4(米),
∴CF=400+141.4≈541(米).
∴山峰的高度 CF大约是541米.
2
1
2
2
2 100 2
5.热气球的探测器显示,从热气球底部A处看一
栋高楼顶部的仰角为30°,看这栋楼底部的俯角为
60°,热气球A处与高楼的水平距离为120m,这栋
高楼有多高?(结果取整数,参考数据: ≈1.73)3
解:过点A作AD⊥BC,垂足为点D.
在Rt△ABD中,∵∠BAD=30°,AD=120 m,
∴BD=AD·tan30°=120× m,
在Rt△ACD中,∵∠CAD=60°,AD=120 m,
∴CD=AD, tan60°=120× =120 m,
BC=160 ≈277 m.
∴这栋高楼的高度是277 m.
3 40 33
3 3
3
相关文档
- 2018届二轮复习书面表达从高考试题2021-04-16 14:38:2931页
- 人教版小升初数学课件综合测试卷(2021-04-16 14:38:1423页
- 2020届 二轮复习 微专题突破:微专题2021-04-16 14:38:0067页
- 2019秋人教部编版七年级语文上册课2021-04-16 14:37:4320页
- 2021届新高考语文一轮课件:第三部分2021-04-16 14:36:3979页
- 历史部编版9年级上册同步课件第6课2021-04-16 14:36:3512页
- 二年级上册数学课件-第7单元:表内乘2021-04-16 14:35:3321页
- 二年级数学下册第九单元《我是体育2021-04-16 14:35:0415页
- 通用版七年级道德与法治上册第四单2021-04-16 14:34:3827页
- 高中物理人教版必修2课件第7章 7动2021-04-16 14:33:5724页