- 424.92 KB
- 2021-04-16 发布
唐山市 2018—2019 学年度高三年级摸底考试
理科数学
一、选择题:本题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合题目
要求的.
1.已知集合 2{ | 5 6 0}, { | 0 8}≤ ≤A x x x B x x ,则 A B ( )
A.[0,6) B.[0,1) C.(0,6) D.( 1,8]
1.答案:A
解析: 2{ | 5 6 0} { | 1 6}, { | 0 8}, [0,6)≤ ≤A x x x x x B x x A B .
2.设 i(1 2i)
2 iz
,则 z ( )
A. 5 B.2 C. 41
5 D.1
2.答案:D
解析: i(1 2i) i 1 2ii(1 2i) 5 12 i 2 i 2 i 5
z
.
3.等差数列{ }na 的前 n 项和为 nS ,若 3 11 4a a ,则 13S ( )
A.13 B.26 C.39 D.52
3.答案:B
解析:由等差数列的性质可知, 1 13
1 13 3 11 13
13( )4, 262
a aa a a a S .
4.随机变量 服从正态分布 2( , )N ,若 ( 2) 0.2, (2 6) 0.6P P ,则 ( )
A.6 B.5 C.4 D.3
4.答案:C
解析: ( 6) ( 2) (2 6) 0.8, ( 6) 1 ( 6) 0.2P P P P P ,
( 2) ( 6)P P , 2 6 42 .
5.cos105 cos15 ( )
A. 2
2 B. 2
2 C. 6
2 D. 6
2
5.答案:D
解析:解法一
3 2 6cos105 cos15 cos(60 45 ) cos(60 45 ) 2sin 60 sin 45 2 2 2 2 .
解法二
6cos105 cos15 sin15 cos15 (sin15 cos15 ) 2 sin(45 15 ) 2 sin 60 2
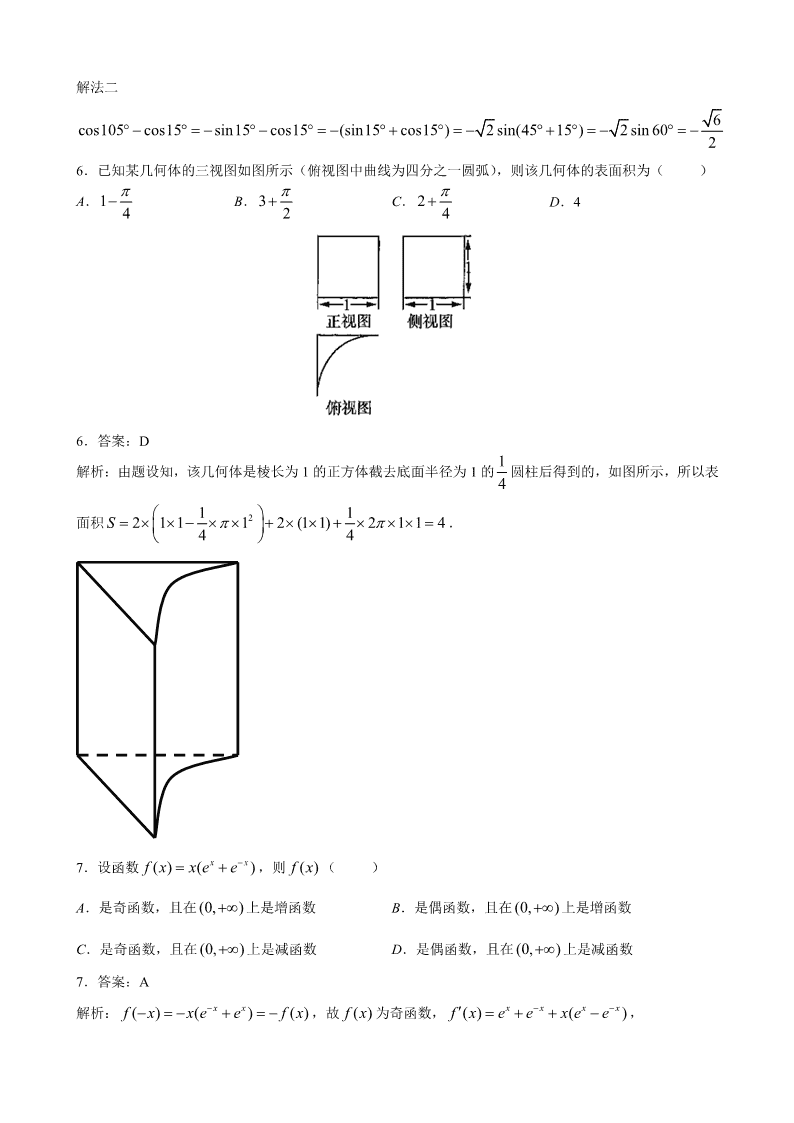
6.已知某几何体的三视图如图所示(俯视图中曲线为四分之一圆弧),则该几何体的表面积为( )
A.1 4
B.3 2
C. 2 4
D.4
6.答案:D
解析:由题设知,该几何体是棱长为 1 的正方体截去底面半径为 1 的 1
4
圆柱后得到的,如图所示,所以表
面积 21 12 1 1 1 2 (1 1) 2 1 1 44 4S
.
7.设函数 ( ) ( )x xf x x e e ,则 ( )f x ( )
A.是奇函数,且在(0, ) 上是增函数 B.是偶函数,且在(0, ) 上是增函数
C.是奇函数,且在(0, ) 上是减函数 D.是偶函数,且在(0, ) 上是减函数
7.答案:A
解析: ( ) ( ) ( )x xf x x e e f x ,故 ( )f x 为奇函数, ( ) ( )x x x xf x e e x e e ,
当 0x 时, x xe e ,所以 ( ) 0x xx e e ,又 0x xe e ,所以 ( ) 0f x ,所以 ( )f x 在 (0, ) 上是
增函数.
8.已知 1 2,e e
是两个单位向量, 1 2e e
的最小值为 3
2
,则 1 2e e
( )
A.1 B. 3 C.1 或 3 D.2
8.答案:C
解析:设向量 1 2,e e
的夹角为 ,则
2 2 22 2
1 2 1 1 2 22 cos 2cos 1e e e e e e
,
当 cos 时,
2
1 2e e
取得最小值 2 3 11 cos , cos4 2 ,故
2
1 2 2 2cos 1e e
或 3,
所以 1 2 1e e
或 3 .
9.已知程序框图如图所示,则该程序框图的功能是( )
A.求 1 1 1 11 3 5 7 21 的值 B.求 1 1 1 11 3 5 7 19 的值
C.求 1 1 1 11 3 5 7 19 的值 D.求 1 1 1 11 3 5 7 21 的值
9.答案:C
解析:执行程序框图, 1 1 11, 1, 3; 1 , 1, 5; 1 , 1, 7;3 3 5S a n S a n S a n
1 1 1 11 , 1, 21 193 5 7 19S a n 满足条件,退出循环,故该程序框图的功能是求
1 1 1 11 3 5 7 19 的值.
10.已知椭圆
2 2
2 2: 1( 0)x yC a ba b 和双曲线 2 2: 1E x y 有相同的焦点 1 2,F F ,且离心率之积为 1,
P 为两曲线的一个交点,则 1 2F PF△ 的形状为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
10.答案:B
解析:双曲线的离心率为 2 ,所以椭圆的离心率 2
2
ce a ,又因为 2c ,所以 2, 2a b ,
由 1 2 1
1 2 2
4 3
2 1
PF PF PF
PF PF PF
,又 1 2 2 2F F ,所以 2 2 2
1 1 2 2PF F F PF ,所以 1 2F PF△ 是直角
三角形.
11.已知函数 ( ) sin sin 3 , [0,2 ]f x x x x ,则 ( )f x 的所有零点之和等于( )
A.5 B.6 C.7 D.8
11.答案:C
解析:解法一:由 ( ) sin sin 3 0f x x x ,得sin sin 3x x ,在同一坐标系中作出函数 siny x 与函
数 sin 3y x 在 [0,2 ]x 上的图象,由图可知,共有 7 个交点,且这 7 个交点关于点( ,0) 对称,
所以 ( )f x 的所有零点之和等于7 .
1
0.5
0.5
1
π
3
2π
3
π 4π
3
5π
3
2π
解法二: ( ) sin sin 3 sin(2 ) sin(2 ) 2cos 2 sinf x x x x x x x x x ,令 ( ) 0f x ,得cos 2 0x
或sin 0x ;由cos 2 0x ,得 2 , , ,2 2 4Z Zkx k k x k ,又 [0,2 ]x ,
3 5 7
4 4 4 4x 或 或 或 ;
由sin 0x ,得 0 2x 或 或 , 3 5 7 0 2 74 4 4 4
.
12.已知三棱锥 P ABC 的四个顶点都在半径为 3 的球面上, AB AC ,则该三棱锥体积的最大值是
( )
A.16
3 B. 32
3 C. 64
3 D.32
12.答案:B
解析:设 ,AB a AC b ,则 1
2ABCS bc△ , ABC△ 所在外接圆的半径
2 2
2
a br ,球心O 到平面
ABC 的距离
2 2
2 2 9 4
a bd R r ,三棱锥体积最大时,
2 2
3 9 4
a bh R d ,
则
2 2 2 2 2 21 1 3 9 3 93 6 2 12 4
≤P ABC ABC
a b a b a bV S h ab
△ (当且仅当 a b 时等号成
立),设
2 2
9 4
a bt ,则0 3≤t ,
2
3 29 1( ) (3 ) ( 3 9 27)3 3
tV t t t t t , 2( ) 2 3 ( 3)( 1)V t t t t t ,
当 0 1≤t 时, ( ) 0, ( )V t V t 单调递增,当1 3t 时, ( ) 0, ( )V t V t 单调递减,
所以当 1t ,即 4a b h 时,三棱锥体积取得最大值 32(1) 3V .
二、填空题:本题共 4 小题,每小题 5 分,共 20 分.把答案填在题中的横线上.
13.已知 ,x y 满足
2 4
2 2
3 3
≥
≥
≤
x y
x y
x y
,则 2z x y 的最大值为 .
13.答案:2
解析:作出可行域为如图所示的 ABC△ ,其中 (0, 2), (1,0), (2,3)A B C ,则 2, 2, 1A B Cz z z ,
max 2Bz z .
O x
y
A
B
C
14.在
5
2 2ax x
的展开式中, 4x 的系数为 5,则实数 a 的值为 .
14.答案: 1
2
解析:由条件可知二项展开式的通项 2 5 5 10 3
1 5 5
2( ) ( 2)
k
k k k k k k
kT C ax C a xx
,令10 3 4k ,得
2k ,故 2 2 3 3 3
5
1 1( 2) 40 5, ,8 2C a a a a .
15.已知直线 : 2 0l kx y k 与圆 2 2: 2 7 0C x y y 相交于 ,A B 两点,则 AB 的最小值为
.
15.答案: 2 6
解析:直线l 的方程为 2 ( 1)y k x ,经过定点 (1,2)P ,由已知的圆C 的标准方程为 2 2( 1) 8x y ,
可知圆心 (0,1)C ,半径 2 2r ,由 2 22AB r d 可知当直线l 与CP 垂直时弦长最小,此时
2d CP ,故 2 2
min 2 (2 2) ( 2) 2 6AB .
4
3
2
1
1
2
2 2
B
A
P
C
O
16. ABC△ 的垂心 H 在其内部, 30 , 3A AH ,则 3BH CH 的取值范围是 .
16.答案:(1, 3)
解析:由已知,得 ABC△ 为锐角三角形,如图,延长 , ,AH BH CH 分别交 , ,BC AC AB 于 , ,E F D ,因
为 H 是垂心,所以 , ,AE BC BF AC CD AB ,又 30BAC ,所以 60ABF ACD .
设 , (0 ,30 )BAH ,则 30CAH ,又 3AH ,
所以在 ABH△ 中,由正弦定理得 2sinsin sin 60
BH AH BH
,
在 ACH△ 中,由正弦定理得 2sin(30 )sin(30 ) sin 60
CH AH CH
.
所以 3 2 3 sin 2sin(30 ) 3 sin cos 2sin(30 )BH CH ,因为 (0 ,30 ) ,
所以 30 (30 ,60 ) ,所以 1 3sin(30 ) , 2sin(30 ) (1, 3)2 2
, ,
即 3 (1, 3)BH CH
A
B C
D
E
FH
三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.第 17~21 题为必考题,每个试题考
生都必须作答.第 22、23 题为选考题,考生根据要求作答.
(一)必考题:共 60 分.
17.(本小题满分 12 分)
已知数列{ }na 的前 n 项和为 nS , 3 1
2
n
n
aS .
(1)求 na ;
(2)若 ( 1)n nb n a ,且数列{ }nb 的前 n 项和为 nT ,求 nT .
17.解析:(1)由已知可得, 2 3 1n nS a , ①
所以 1 12 3 1 ( 2)n nS a n ≥ , ②
①-②得, 1 12( ) 3 3n n n nS S a a ,
化简为 13 ( 2)n na a n ≥ ,即
1
3 ( 2)n
n
a na
≥ , …3 分
在①中,令 1n 可得 1 1a , …4 分
所以数列{ }na 是以 1 为首项,3 为公比的等比数列,
从而有 13n
na . …6 分
(2) 1( 1) 3n
nb n ,
0 1 2 2 1
1 2 3 1
0 3 1 3 2 3 ( 2) 3 ( 1) 3
3 0 3 1 3 2 3 ( 2) 3 ( 1) 3
n n
n
n n
n
T n n
T n n
③
④
③-④得, 1 2 3 12 3 3 3 3 ( 1) 3n n
nT n …8 分
3 3 (3 2 ) 3 3( 1) 31 3 2
n n
n nn . …10 分
所以, (2 3) 3 3
4
n
n
nT . …12 分
18.(本小题满分 12 分)
甲、乙两位工人分别用两种不同工艺生产同一种零件,已知尺寸在[223, 228](单位:mm)内的零件为一
等品,其余为二等品.甲、乙当天生产零件尺寸的茎叶图如图所示:
甲 乙
8 7 21 8 9
8 6 6 5 2 22 1 3 4 5 7 8
4 3 1 23 0 2
(1)从甲、乙两位工人当天生产的零件中各随机抽取 1 个零件,求抽取的 2 个零件等级互不相同的概率;
(2)从工人甲当天生产的零件中随机抽取 3 个零件,记这 3 个零件中一等品数量为 X,求 X 的分布列和
数学期望.
18.解析:(1)由茎叶图可知,甲当天生产了 10 个零件,其中 4 个一等品,6 个二等品;乙当天生产了
10 个零件,其中 5 个一等品,5 个二等品,
所以,抽取的 2 个零件等级互不相同的概率
4 5 6 5 1
10 10 2P
. …5 分
(2)X 可取 0,1,2,3. …6 分
0 3 1 2 2 1 3 0
4 6 4 6 4 6 4 6
3 3 3 3
10 10 10 10
1 1 3 1( 0) ; ( 1) ; ( 2) , ( 3)6 2 10 30
C C C C C C C CP X P X P X P XC C C C ;
…10 分
X 的分布列为
X 0 1 2 3
P 1
6 1
2 3
10 1
30
∴随机变量 X 的期望 1 1 3 1 6( ) 0 1 2 36 2 10 30 5E X . …12 分
19.(本小题满分 12 分)
斜率为 ( 0)k k 的直线l 与抛物线 2y x 交于 1 1 2 2( , ), ( , )A x y B x y 两点,O 为坐标原点.
(1)当 1 2 2x x 时,求 k ;
(2)若OB l ,且 3AB OB ,求 AB .
19.解析:(1)由已知可得, 2 2
1 1 2 2y x y x , ,
所以 2 2
1 2 1 2 1 2 1 2 1 2( )( ) 2( )y y x x x x x x x x ,
此时,直线l 的斜率 1 2
1 2
2y yk x x
. …4 分
(2)因为OB l ,所以 kOB=- 1
k ,
又因为
2
2 2
2
2 2
OB
y xk xx x ,所以, 2
1x k , …6 分
又由(1)可知, 1 2
1 2
1 2
y yx x kx x
,从而有, 1 2
1x k x k k ,
所以 2 2
1 2
21 1AB k x x k k k ,
2
2 2 2 4
2 2 2 2 2 4 2
1 1 1 kOB x y x x k k k
…9 分
因为 3AB OB ,所以
2
2
2
2 3 11 kk k k k
,
化简得, 3 2 3k k |,解得, 1k ,
所以, 2 21 3 2AB k k k . …12 分
20.(本小题满分 12 分)
在直角三角形 ABC 中, 2AB BC , D 为 AC 的中点.如图,以 BD 为折痕将 ABD△ 折起,使点 A
到达点 P 的位置,且 PB CD .
(1)求证: PD 平面 BCD ;
(2)求 PA 与平面 PBC 所成角的正弦值.
P
A
B
CD
20.解析:(1)∵直角三角形 ABC 中,
AB=BC=2,D 为 AC 的中点,
∴BD⊥CD,
又∵PB⊥CD,BD∩PB=B,
∴CD⊥平面 PBD,
∴CD⊥PD,
又∵AD⊥BD,
∴PD⊥BD.
又因为 BD∩CD=D,
∴PD⊥平面 BCD. …5 分
(2)以 D 为坐标原点,DA,DB,DP 所在直线分别为 x 轴,y 轴,z 轴,建立空间直角坐标系 D-xyz,
则 ( 2,0,0), (0, 2,0), ( 2,0,0), (0,0, 2)A B C P ,
( 2,0, 2), (0, 2, 2), ( 2, 2,0)PA PB CB
,
设平面 PBC 的法向量 ( , , )n x y z ,
由 2 2 0
2 2 0
n PB y z
n CB x y
,可取 (1, 1, 1)n . …9 分
6cos , 3
PA nPA n
PA n
,∴直线 PA 与平面 PBC 所成角的正弦值为 6
3
. …12 分
21.(本小题满分 12 分)
已知函数 1( ) log ( 0af x x ax ,且 1)a .
(1)当 a e 时,曲线 ( )y f x 与直线 y m 相切,求 m 的值;
(2)若 ( )≥ ef x a
,求 a 的取值范围.
(1)当 a e 时, 1( ) lnf x x x ,所以 2 2
1 1 1( ) xf x x x x
. …1 分
设切点为 0 0( , ( ))x f x ,曲线 ( )y f x 与 y m 相切,得 0( ) 0f x ,
A B
C
P
D
x y
z
解得 0 1x ,所以切点为(1,1) . …3 分
所以 1m . …4 分
(2)依题意得 (1) ef a
≥ ,所以1 e
a
≥ ,从而 a e≥ . …5 分
因为 2
ln( ) ,ln
x af x a ex a
≥ ,
所以当0 lnx a 时, ( ) 0f x , ( )f x 单调递减;当 lnx a 时, ( ) 0f x , ( )f x 单调递增,
所以当 lnx a , ( )f x 取得最小值 1log (ln ) lna a a . …7 分
设 ( ) ln ,g x e x x x ≥e ,则 ( ) 1e e xg x x x
≤0 ,
所以 ( )g x 在[ , )e 单调递减,从而 ( ) ( ) 0≤g x g e ,所以 lne x x≤ . …10 分
又 a e≥ ,所以 lne a a≤ ,从而 1
ln
e
a a
≥ ,当且仅当 a e 时等号成立.
因为ln 1a≥ ,所以log (ln ) 0a a ≥ ,即 1log (ln ) lna
ea a a ≥ .
综上,满足题设的 a 的取值范围为[ , )e . …12 分
(二)选考题:共 10 分.请考生在第 22、23 题中任选一题作答.如果多做,则按所作的第一题计分.
22.【选修 4—4:坐标系与参数方程】(本小题满分 10 分)
在极坐标系中,曲线C 的方程为 2 2 2 sin 4 04
,以极点O 为原点,极轴为 x 轴正半轴建
立平面直角坐标系 xOy ,直线 cos: sin
x tl y t
(t 为参数,0≤ ).
(1)求曲线C 的直角坐标方程;
(2)设直线l 与曲线C 相交于 ,A B 两点,求 OA OB 的取值范围.
22.(1)由 2 2 2 sin 4 04
得, 2 2 cos 2 sin 4 0 .
所以 2 2 2 2 4 0x y x y .曲线 C 的直角坐标方程为 2 2( 1) ( 1) 6x y . …5 分
(2)将直线 l 的参数方程代入 2 2 2 2 4 0x y x y 并整理得,
2
1 2 1 2
1 2 1 2
2(sin cos ) 4 0, 2(sin cos ), 4 0.
2(sin cos ) 2 2 sin 4
t t t t t t
OA OB t t t t
因为0 ≤ ,所以 5
4 4 4
≤ ,从而有 2 2 2 sin 2 24
≤ .
所以 OA OB 的取值范围是[0, 2 2]. …10 分
23.【选修 4—5:不等式选讲】(本小题满分 10 分)
已知 ( ) 1 2 1f x x x .
(1)求不等式 ( ) 0f x 的解集;
(2)若 Rx 时,不等式 ( )≤f x a x 恒成立,求 a 的取值范围.
23.(1)由题意得 1 2 1x x , 所以 2 21 2 1x x ,
整理可得 2 2 0x x ,解得0 2x ,故原不等式的解集为{ | 0 2}x x . …5 分
(2)由已知可得, ( )a f x x≥ 恒成立,
设 ( ) ( )g x f x x ,则
2, 1
1( ) 2 , 1 2
12 2, 2
x
g x x x
x x
≤ ≤
由 ( )g x 的单调性可知, 1
2x 时, ( )g x 取得最大值 1,
所以 a 的取值范围是[1, ) . …10 分