- 1.36 MB
- 2021-04-16 发布
临川二中2018届高三上学期第五次月考
数学试题(文)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设全集是实数集,,,则如图所示的阴影部分所表示的集合是( )
A. B. C. D.
2.已知复数(为虚数单位),则复数在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.设曲线在点处的切线方程为,则( )
A.0 B.1 C.2 D.3
4.下列说法正确的是( )
A.“”是“”的充分不必要条件
B.命题“,”的否定是:“,”
C. 若为假命题,则均为假命题
D.若为上的偶函数,则的图象关于直线对称
5.已知,则的值为( )
A. B. C. D.
6.下列函数中,与函数的定义域,单调性与奇偶性均一致的函数是( )
A. B. C. D.
7.设等差数列的前项和为,若,,则满足的正整数为( )
A.2013 B.2014 C.2015 D.2016
8.将函数的图象向左平移个单位,再把所有点的横坐标伸长到原来的2倍,得到函数的图象,则下列关于函数的说法错误的是( )
A.最小正周期为 B.图象关于直线对称
C. 图象关于点对称 D.初相为
9.某几何体的三视图如图所示,则该几何体的体积是( )
A. B. C. D.
10.执行如图所示的程序框图,则输出的值为( )
A. B. C. D.
11.设函数满足()且,则为( )
A.95 B.97 C.105 D.392
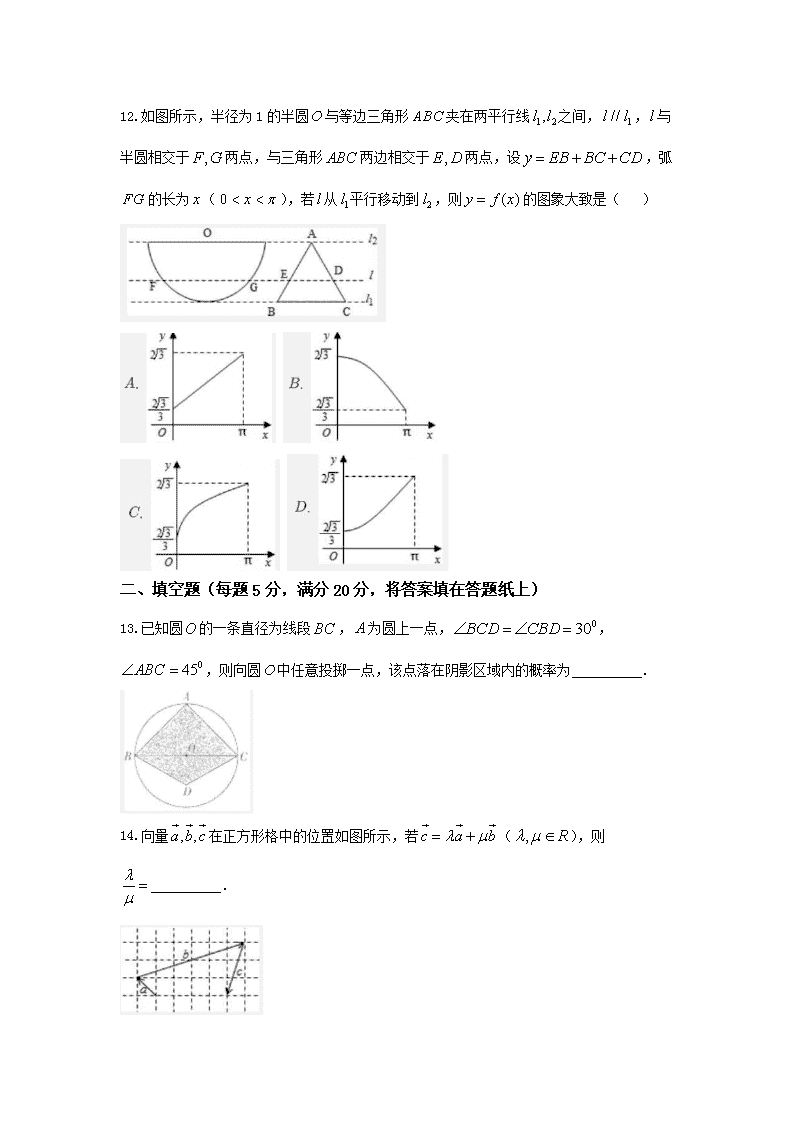
12.如图所示,半径为1的半圆与等边三角形夹在两平行线之间,,与半圆相交于两点,与三角形两边相交于两点,设,弧的长为(),若从平行移动到,则的图象大致是( )
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.已知圆的一条直径为线段,为圆上一点,,,则向圆中任意投掷一点,该点落在阴影区域内的概率为 .
14.向量在正方形格中的位置如图所示,若(),则 .
15.在《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,若四棱锥为阳马,侧棱底面,且,则该阳马的外接球与内切球表面积之和为 .
16.已知椭圆()的左、右焦点分别为,,若椭圆上存在点使成立,则该椭圆的离心率的取值范围为 .
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. 据统计,目前微信用户已达10亿,2016年,诸多传统企业大佬纷纷尝试进入微商渠道,让这个行业不断地走向正规化、规范化.2017年3月25日,第五届中国微商博览会在山东济南舜耕国际会展中心召开,力争为中国微商产业转型升级,某品牌饮料公司对微商销售情况进行中期调研,从某地区随机抽取6家微商一周的销售金额(单位:百元)的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)若销售金额(单位:万元)不低于平均值的微商定义为优秀微商,其余为非优秀微商,根据茎叶图推断该地区110家微商中有几家优秀?
(2)从随机抽取的6家微商中再任取2家举行消费者回访调查活动,求恰有1家是优秀微商的概率.
18. 已知数列的前项和,正项等比数列中,,.
(1)求数列,的通项公式;
(2)若是与的等比中项,求数列的前项和
19. 如图,在矩形中,,,平面,分别为的中点,点是上一个动点.
(1)当是中点时,求证:平面平面;
(2)当时,求的值.
20. 如图,抛物线的焦点为,抛物线上一定点.
(1)求抛物线的方程及准线的方程;
(2)过焦点的直线(不经过点)与抛物线交于两点,与准线交于点,记的斜率分别为,,,问是否存在常数,使得成立?若存在,求出的值;若不存在,说明理由.
21. 已知函数(为常数),函数,(为常数,且).
(1)若函数有且只有1个零点,求的取值的集合.
(2)当(1)中的取最大值时,求证:.
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-4:坐标系与参数方程
在直角坐标系中,曲线的参数方程是(为参数),以坐标原点
为极点,轴正半轴为极轴,建立极坐标系.
(1)求曲线的极坐标方程;
(2)设,,若与曲线分别交于异于原点的两点,求的面积.
23.选修4-5:不等式选讲
已知函数.
(1)解不等式;
(2)记的最小值是,正实数满足,求的最小值.
临川二中2018届高三上学期第五次月考数学答案(文)
一,选择题
CDDDB DBCAB
二,填空题
13. (3+√3)/ 3π 14. 4
15. 16.(√2-1,1)
三,解答题
17.解(1),
(2)
18.解(1)
(2)
19. 解(1)∵分别是矩形的对边的中点,
∴,∴四边形是平行四边形,∴.
又平面,平面,∴平面,
又是中点,∴,
∵平面,平面,∴平面,
∵,平面,∴平面平面.
(2)连接,∵平面,平面,∴.
∵,,平面,∴平面,
∵平面,∴,
在矩形中,由得与相似,∴,
又,∴,∴
20.解 (1)把Q(1,2)代入y2=2px,得2p=4,
所以抛物线方程为y2=4x,
准线l的方程为x=-1.
(2)由条件可设直线AB的方程为y=k(x-1),k≠0.
由抛物线准线l:x=-1,可知M(-1,-2k).
又Q(1,2),所以k3==k+1,
把直线AB的方程y=k(x-1),代入抛物线方程y2=4x,并整理,可得k2x2-2(k2+2)x+k2=0,设A(x1,y1),B(x2,y2),则x1+x2=,x1x2=1,
又Q(1,2),则k1=,k2=.
因为A,F,B三点共线,所以kAF=kBF=k,
即=k,所以k1+k2==2(k+1),
即存在常数λ=2,使得k1+k2=2k3成立.
21.解 (1)f′(x)=,
①当k≤0时,f′(x)>0,则f(x)在(0,+∞)单调递增.
而f(ek-2)=k-2-kek-2+1=k(1-ek-2)-1≤-1<0,f(1)=1-k>0,
故f(x)在(ek-2,1)上存在唯一零点,满足题意;
②当k>0时,令f′(x)>0得0,则f(x)在上单调递减;
若f=0,得k=1,显然满足题意;
若f>0,则00,得x<1,故h(x)在(0,1)上单调递增;
令h′(x)<0,得x>1,故h(x)在(1,+∞)上单调递减;
故h(x)≤h(1)=0,则h=ln-+1<0,
即ln-<-1,
则f=2ln-+1=2+1<-1<0.
故f(x)在上有唯一零点,在上有唯一零点,不符题意.
综上,k的取值的集合为{k|k≤0或k=1}.
(2)由 (1)知,lnx≤x-1,当且仅当x=1时取“=”,
而x+1>1,故lnaxex-ax-2lnx+2x-2=axex-2lnx-2x-2
记F(x)=axex-2lnx-2x-2,
则F′(x)=(x+1)=(axex-2),
令G(x)=axex-2,则G′(x)=a(x+1)ex>0,故G(x)在(0,+∞)上单调递增.
而G(0)=-2<0,G=2(-1)>0,故存在x0∈,
使得G(x0)=0,即ax0-2=0.
则x∈(0,x0)时,G′(x)<0,故F′(x)<0;x∈(x0,+∞)时,G′(x)>0,
故F′(x)>0.
则F(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,
故F(x)≥F(x0)=ax0-2x0-2lnx0-2=-2(x0+lnx0)=-2ln(x0)
=-2ln=2lna-2ln2.
故ag(x)-2f(x)>2(lna-ln2).
22.解:(Ⅰ)将C的参数方程化为普通方程为(x-3)2+(y-4)2=25,
即x2+y2-6x-8y=0.
∴ C的极坐标方程为.
(Ⅱ)把代入,得,6分
把代入,得,∴…8分
∴ S△AOB…10分
23.解:(Ⅰ)当x≤时,f(x)=-2-4x,
由f(x)≥6解得x≤-2,综合得x≤-2,
当时,f(x)=4,显然f(x)≥6不成立,
当x≥时,f(x)=4x+2,由f(x)≥6解得x≥1,综合得x≥1,
所以f(x)≥6的解集是.
(Ⅱ)=|2x-1|+|2x+3|≥,
即的最小值m=4.
∵ ≤,
由可得≤,解得≥,
∴ 的最小值为.