- 830.50 KB
- 2021-04-16 发布
广西柳州二中2019-2020学年高二下学期5月周测3(文)
一、单选题:
1.已知集合,则( )
A. B. C. D.
2.设,则( ) A. B. C. D.
3.已知命题P:,则为( )
A. B.
C. D.
4.已知角的终边在直线上,则( )
A. B. C. D.
5.已知,令,,,那么之间的大小关系为( )
A. B. C. D.
6.设是函数的导函数,的图象如图所示,则的图象最有可能的是( )
A. B. C. D.
7.双曲线的渐近线方程为( )
A. B. C. D.
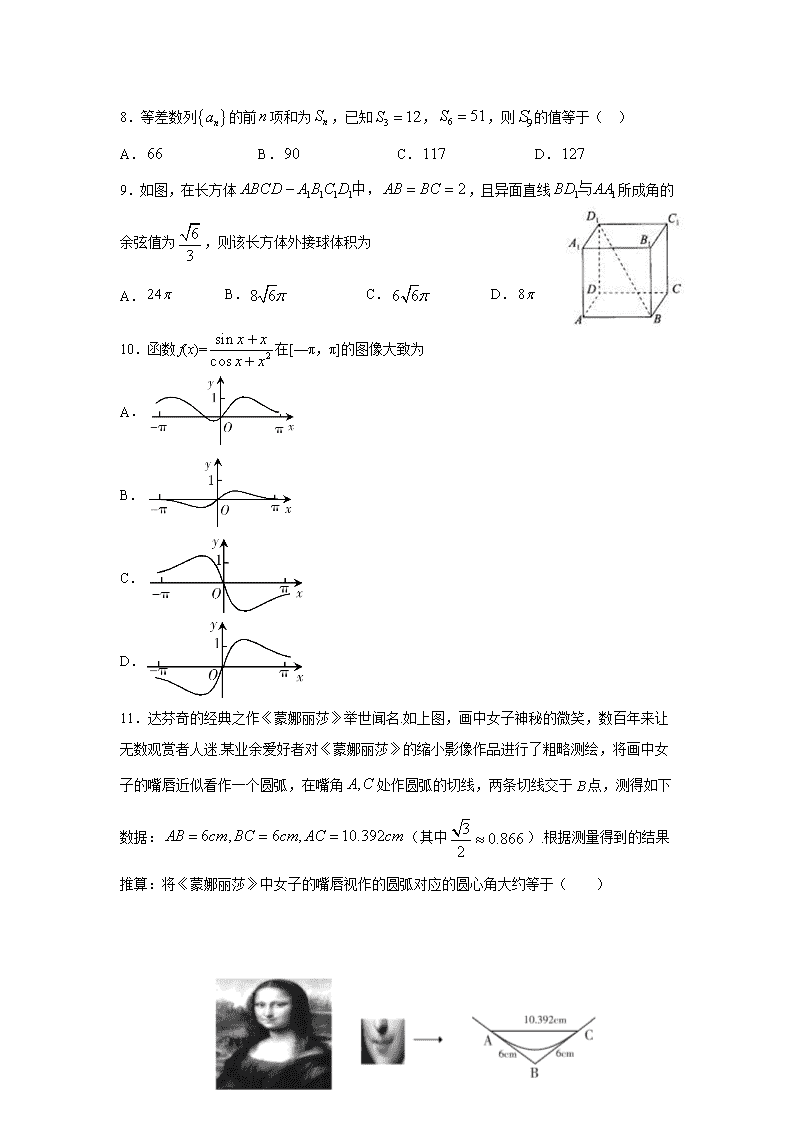
8.等差数列的前项和为,已知,,则的值等于( )
A. B. C. D.
9.如图,在长方体,且异面直线所成角的余弦值为,则该长方体外接球体积为
A. B. C. D.
10.函数f(x)=在[—π,π]的图像大致为
A.
B.
C.
D.
11.达芬奇的经典之作《蒙娜丽莎》举世闻名.如上图,画中女子神秘的微笑,数百年来让无数观赏者人迷.某业余爱好者对《蒙娜丽莎》的缩小影像作品进行了粗略测绘,将画中女子的嘴唇近似看作一个圆弧,在嘴角处作圆弧的切线,两条切线交于点,测得如下数据:(其中).根据测量得到的结果推算:将《蒙娜丽莎》中女子的嘴唇视作的圆弧对应的圆心角大约等于( )
A. B. C. D.
12.已知是上的偶函数,且在上单调递减,则不等式的解集为( )
A. B. C. D.
二、填空题:
13.已知实数满足约束条件,则的最大值为_______.
14.已知平面向量与的夹角为,, ,则__________.
15.若,均为正数,且1是,的等差中项,则的最大值为______.
16.已知抛物线与直线交于两点,则弦长
_______________.
三、解答题
17.已知向量,,设函数,.
(1)求的最小正周期和最大值;(2)讨论在区间上的单调性.
18.在等比数列中,,,
(1)求数列的通项公式;(2)求.
19.如图,矩形中,平面,,为上的点,且平面,,交于点.
(1)求证:平面; (2)求三棱柱的体积.
20.某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价和月销售量之间的一组数据,如下表所示:
(Ⅰ)根据统计数据,求出关于的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;(Ⅱ)现用样本估计总体,从上述5个销售单价中任选2个销售单价,求抽到的产品含有月销量量不低于10万件的概率.
附:, 参考数据:,.
参考答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
C
B
A
C
B
C
B
D
A
B
13.6 14. 15. 1 16.
17.已知向量,,设函数,.
(1)求的最小正周期和最大值;(2)讨论在区间上的单调性.
解:(1)因为向量,
则
由周期公式可得最小正周期为 ,由可得的最大值为
(2) 因为,则
由正弦函数的图像可知,当时为单调递增,此时
当时为单调递减,此时
综上可知,当时单调递增; 当时, 单调递减
18.在等比数列中,,,
(1)求数列的通项公式;(2)求.
解:(1)因为数列是等比数列,,可得,,
解得, 所以
(2)令,
所以数列是以为首项,为公比的等比数列,
所以
.
19、如图,矩形中,平面,,为上的点,且平面,,交于点.
(1)求证:平面;
(2)求三棱柱的体积.
(1)证明:∵平面,,
∴平面,又平面,则,
又∵平面,平面,,
平面,平面,
∴平面.
(2)解:由(1)知,而平面,
∴平面,∴平面.
∵是中点,是中点,
平面,,则△CBE为直角三角形,
∴,.
20. 某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价和月销售量之间的一组数据,如下表所示:
(Ⅰ)根据统计数据,求出关于的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;(Ⅱ)现用样本估计总体,从上述5个销售单价中任选2个销售单价,求抽到的产品含有月销量量不低于10万件的概率.
附:, 参考数据:,.
【详解】
(Ⅰ)∵,,
∴,则,
∴回归直线方程为,
要使月销售量不低于12万件,则有,解得,
∴月销售单价的最大值为8.75元;
(Ⅱ)由题意可得销售单价共有5个,其中使得月销售量不低于10万件的有2个,记为,月销售量不低于8万件不足10万件的有1个,记为
,月销售量低于8万件的有2个,记为,从中任取2个有:共10个,抽到的产品含有月销量量不低于10万件的有7个,∴所求概率为.