- 788.00 KB
- 2021-04-16 发布
沈阳铁路实验中学2017——2018学年度下学期期中试题
高二(文)数学
时间:120分钟 分数:150分
命题人:裴晓航 校对:殷裕民
一、单选题(每题5分,共12道题,满分60分)
1.已知全集,集合,,则( )
A. B. C. D.
2.已知复数(其中为虚数单位),则在复平面内对应的点在( )
A. 第一象限 B. 第三象限 C. 直线上 D. 直线上
3.“”是“”的( )
A. 充要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分也不必要条件
4.(2018·合肥一模)用反证法证明某命题时,对结论:“自然数a,b,c中恰有一个是偶数”的正确假设为( )
A. 自然数a,b,c中至少有两个偶数 B. 自然数a,b,c中至少有两个偶数或都是奇数
C. 自然数a,b,c都是奇数 D. 自然数a,b,c都是偶数
5.下列图形中表示两个变量具有线性相关关系的是
A. B. C. D.
6.在2018年石嘴山市高中生研究性学习课题展示活动中,甲、乙、丙代表队中只有一个队获得一等奖,经询问,丙队代表说:“甲代表队没得—等奖”;乙队代表说:“我们队得了一等奖”;甲队代表说:“丙队代表说的是真话”。事实证明,在这三个代表的说法中,只有一个说的是假话,那么获得一等奖的代表队是( )
A. 甲代表队 B. 乙代表队 C. 丙代表队 D. 无法判断
7.下列说法中正确是( )
A. 若命題,使得,则,均有
B. 若“”是真命题,则一定是真命题
C. 已知则“”是“”的必要不充分条件
D. 命题“若”,则的逆命题是真命题
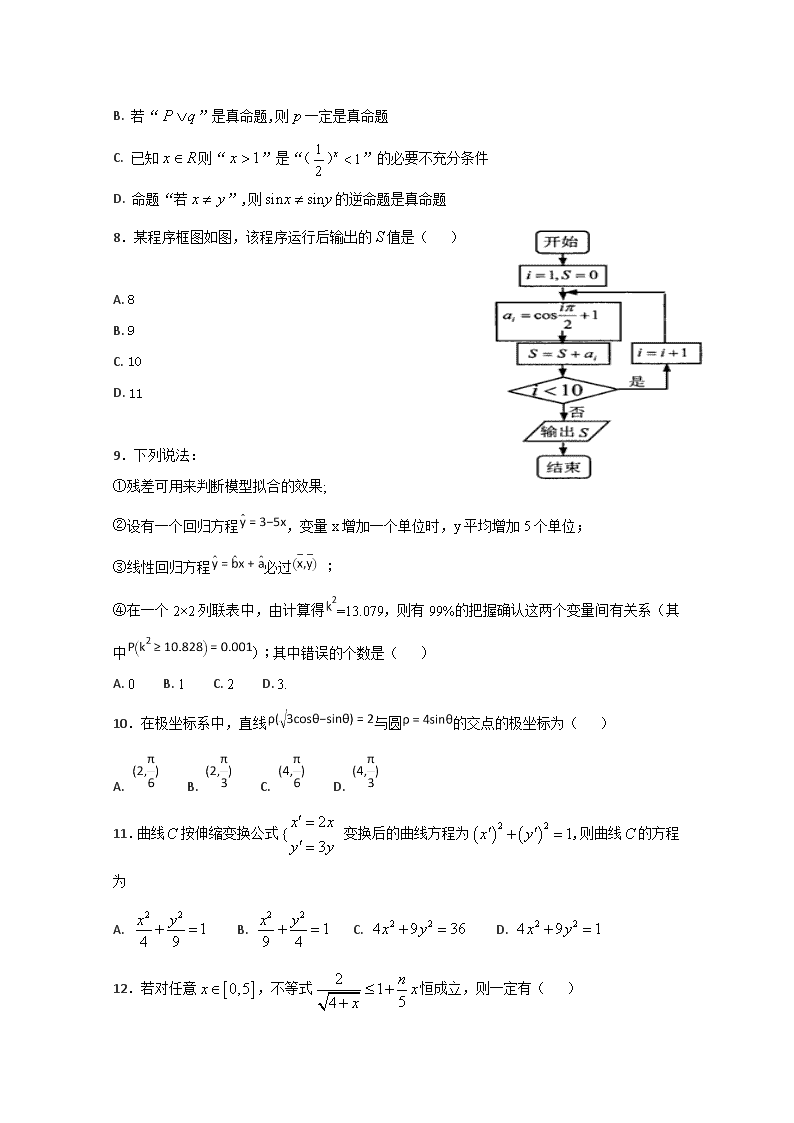
8.某程序框图如图,该程序运行后输出的值是( )
A. 8
B. 9
C. 10
D. 11
9.下列说法:
①残差可用来判断模型拟合的效果;
②设有一个回归方程,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程必过 ;
④在一个2×2列联表中,由计算得=13.079,则有99%的把握确认这两个变量间有关系(其中);其中错误的个数是( )
A. 0 B. 1 C. 2 D. 3.
10.在极坐标系中,直线与圆的交点的极坐标为( )
A. B. C. D.
11.曲线按伸缩变换公式变换后的曲线方程为,则曲线的方程为
A. B. C. D.
12.若对任意,不等式恒成立,则一定有( )
A. B. C. D.
二、填空题(每题5分,共4道题,满分20分)
13.若复数(,为虚数单位)是纯虚数,则实数__________.
14.关于的不等式对一切恒成立,则实数取值的集合为______.
15.观察下列数字的排列规律:,则第个数字是______
16.已知命题, 恒成立,命题,使得,若命题为真命题,则实数的取值范围为__________.
三、解答题(共6道题,满分70分)
17.(本小题满分12分)在党的第十九次全国代表大会上,习近平总书记指出:“房子是用来住的,不是用来炒的”.为了使房价回归到收入可支撑的水平,让全体人民住有所居,近年来全国各一、二线城市打击投机购房,陆续出台了住房限购令.某市一小区为了进一步了解已购房民众对市政府出台楼市限购令的认同情况,随机抽取了本小区 50 户住户进行调查,各户人平均月收入(单位:千元,)的户数频率分布直方图如下图:
其中,赞成限购的户数如下表:
人平均月收入
赞成户数
4
9
12
6
3
1
(1)求人平均月收入在的户数,若从他们中随机抽取两户,求所抽取的两户都赞成楼市限购令的概率;
(2)求所抽取的 50户的人平均月收入的平均数;
(3)若将小区人平均月收入不低于7千元的住户称为“高收入户”,人平均月收入低于7千元的住户称为“非高收入户”.根据已知条件完成如图所给的列联表,并说明能否在犯错误的概率不超过 0.01 的前提下认为“收入的高低”与“赞成楼市限购令”有关.
非高收入户
高收入户
总计
赞成
不赞成
总计
附:临界值表
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
参考公式:.
18.(本小题满分12分)某高三理科班共有60名同学参加某次考试,从中随机挑选出5名同学,他们的数学成绩与物理成绩如下表:
数据表明与之间有较强的线性关系.
(1)求关于的线性回归方程;
(2)该班一名同学的数学成绩为110分,利用(1)中的回归方程,估计该同学的物理成绩;
(3)本次考试中,规定数学成绩达到125分为优秀,物理成绩达到100分为优秀.若该班数学优秀率与物理优秀率分别为和,且除去抽走的5名同学外,剩下的同学中数学优秀但物理不优秀的同学共有5人.能否在犯错误概率不超过0.01的前提下认为数学优秀与物理优秀有关?
参考数据:回归直线的系数,.
,.
19.(本小题满分12分)已知直线为参数),圆 (为参数),
(Ⅰ)当时,求与的交点坐标;
(Ⅱ)过坐标原点作的垂线,垂足为, 为的中点,当变化时,求点轨迹的参数方程,并指出它是什么曲线.
20.(本小题满分12分)已知点,参数,点Q在曲线C: 上.
(Ⅰ)求在直角坐标系中点的轨迹方程和曲线C的方程;
(Ⅱ)求|PQ|的最大值.
21.(本小题满分12分)选修4-5:不等式选讲
已知函数.
(I)求不等式的解集;
(Ⅱ)若正数满 足求证: .
22.(本小题满分10分)(1)已知中至少有一个小于2。
(2)已知,求证:.
参考答案
1.A
2.C
3.B
4.B
5.C
【解析】A,B是确定的函数关系图象.由C,D的散点图,可知若样本点成带状分布,则两个变量具有线性相关关系,所以两个变量具有线性相关关系的图是C.故选C.
6.B
【解析】由题设中提供的算法流程图可知程序执行的是求和运算:由于的周期是,所以,应选答案B。
7.C
【解析】若丙说的是假话,则甲获得了一等奖,那么乙说的也是假话,故不对;若乙说假话了,则甲丙说的都是真话,那丙获得了一等奖,符合题意;若甲说的是假话,则则丙说的也是假话,不合题意,故也不正确.
故答案为:C.
8.D
【解析】 由题意,A中,命题使得,则使得,所以不正确;
B中,若“”是真命题,则中至少有一个为真命题,所以不正确;
C中,已知,则“”是“”的充要条件,所以不正确;
D中,命题:“若”,则“”的逆命题为:“若”,则“”是正确的,故选D.
9.B
【解析】对于①,根据方差是表示一组数据波动大小的量,将一组数据中的每个数据都加上或减去同一个常数后,方差不变,①正确;对于②,有一个回归方程,变量增加一个单位时,平均减少个单位,②错误;对于③,根据线性回归方程的性质可得必过样本中心点,③正确;对于④,在列联表中,计算得,对照临界值表知,有的把握确认这两个变量间有关系,④正确,故选B.
10.A
【解析】联立,解得.
则直线与圆交点的极坐标为.
本题选择A选项.
11.D
【解析】由题意,把伸缩变换公式代入曲线方程为x/2+y/2=1,
得(2x)2+(3y)2=1,即4x2+9y2=1.
∴曲线c的方程为4x2+9y2=1.
故选:D.
12.A
【解析】原命题转化为 ,令 设, 原函数可化为 ,故选A.
13.6
【解析】 为纯虚数,故
14.
【解析】由题意,构造二次函数,易知其图象开口向上,且当时,有,则,即,得,所以当时,不等式成立,故正确答案为.
点睛:此题主要考查二次函数最值的性质在二次不等式恒成立问题中的应用,以及二次不等式的求解等有关方面的知识与运算技能、转化思想,属于中档题型,也是常考考点.不等式恒成立问题是数学中非常典型问题,也是历年高考的热点题型之一,确定不等式恒成立中参数的取值范围,需要灵活应用函数与不等式的基础知识,并时常要在两者间进行合理的交汇.
15.2
【解析】若把012看成一组数字,则第一组有1个0,2个1,3个2,共6个数字;第二组有4个0,5个1,6个2,共15个数字;猜测第三组有7个0,8个1,9个2,共24个数字;所以, ;令 ,解得 是其最大的整数解,此时故第2007个数字是时的数字,应为2;
故答案为2.
【点睛】本题考查了数列的探究规律型问题,根据题目中的数字排列情况,探究其中的规律,利用所学的知识,作出解答.
16.
【解析】当P为真命题时, 恒成立,所以, ,当Q为假命题时, 为真命题,即,所以,又命题为真命题,所以命题都为真命题,则 ,即。故实数的取值范围是。
17.(1);(2)6.4千元;(3)答案见解析.
【解析】试题分析:(1)根据均值公式计算即可;(2)
住户共有8户,赞成楼市限购令的有4户,从中随机抽取两户,随机变量的取值可能为0,1,2,分别计算其概率即可;(3)根据卡方公式计算即可得出结论.
试题解析:
(1)千元
(1)由直方图知:月收入在的住户共有8户,赞成楼市限购令的有4户,从中随机抽取两户,设为赞成楼市限购令的用户数.
则
所以的分布列为:
0
1
2
P
(3)依题意,列联表如下
非高收入户
高收入户
总计
赞成
25
10
35
赞成
5
10
15
总计
30
20
50
所以不能在犯错误的概率不超过的前提下认为“收入的高低”与“赞成楼市限购令”有关.
18.(1)(2)82(3)可以认为
【解析】试题分析:(1)由表格得到 ,进而得到 , ,从而得到关于的线性回归方程;(2) 将代入上述方程,得;(3)列出2×2列联表,求出,从而作出判断.
试题解析:
(1)由题意可知,
故 .
,
故回归方程为.
(2)将代入上述方程,得.
(3)由题意可知,该班数学优秀人数及物理优秀人数分别为30,36.
抽出的5人中,数学优秀但物理不优秀的共1人,
故全班数学优秀但物理不优秀的人共6人.
于是可以得到列联表为:
于是,
因此在犯错误概率不超过0.01的前提下,可以认为数学优秀与物理优秀有关.
点睛:本题主要考查线性回归方程,属于难题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算的值;③计算回归系数;④写出回归直线方程为; 回归直线过样本点中心是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
19.(Ⅰ), (Ⅱ)点是圆心为,半径为的圆
【解析】试题分析:(Ⅰ)求得的普通方程, 联立方程组,解之得正解;
(Ⅱ)求得的普通方程 点坐标为点轨迹的参数方程为
(为参数) 点轨迹的普通方程为 故点是圆心为,半径为的圆.
试题解析:
(Ⅰ)当时, 的普通方程为, 的普通方程为
. 联立方程组解得与的交点为,
(Ⅱ)的普通方程为. 点坐标为,故当变化时, 点轨迹的参数方程为
(为参数)
点轨迹的普通方程为 故点是圆心为,半径为的圆.
20.(Ⅰ)(Ⅱ)
【解析】试题分析:(Ⅰ)消参得点的轨迹是上半圆: ,再利用公式求得:曲线C的直角坐标方程: ;(Ⅱ)所求最大值就是点到直线
的距离.
试题解析:
(Ⅰ)设,则,点的轨迹是上半圆: 曲线C的直角坐标方程: 分
(Ⅱ)|PQ|的最大值就是点到直线的距离,
21.(Ⅰ);(Ⅱ)见解析.
【解析】试题分析:(Ⅰ)将不等式转化为.
法一:由绝对值不等式的几何意义,可得不等式的解集;
法二:分类讨论,去掉绝对值号,分别求解不等式组,进而得到不等式的解集;
(Ⅱ)由题意,得到,利用绝对值的三角不等式,即可作出证明.
试题解析:
(Ⅰ)此不等式等价于.
法一:由绝对值不等式的几何意义得不等式的解集为.
法二:由 或或
或或不等式的解集为.
(Ⅱ)证明:
当且仅当时取等号.
当且仅当时取等号.∴.
22.(1)见解析(2)见解析
【解析】试题分析:(1)正繁则反,对于至少型问题,一般利用反证法,即假设都不小于2,再利用基本不等式得矛盾,否定假设(2)利用分析法证明条件与结论相差较大的题目,通过不断的转化,将条件与结论最终联系在一起:即去分母,平方,整理成条件形式.
试题解析:(1)证明:假设都不小于2,则
, 即
这与已知矛盾,故假设不成立,从而原结论成立.
(2)
[证明] ∵->1,a>0,∴0,只需证·>1,只需证1+a-b-ab>1,只需证a-b-ab>0,即>1.即->1.这是已知条件,所以原不等式成立.