- 376.50 KB
- 2021-04-16 发布
红兴隆管理局第一高级中学
2017-2018学年度第一学期高二年级期中考试
数学学科试卷
注:卷面分值150分; 时间:120分钟
一、 选择题60分(每题5分,共12小题)
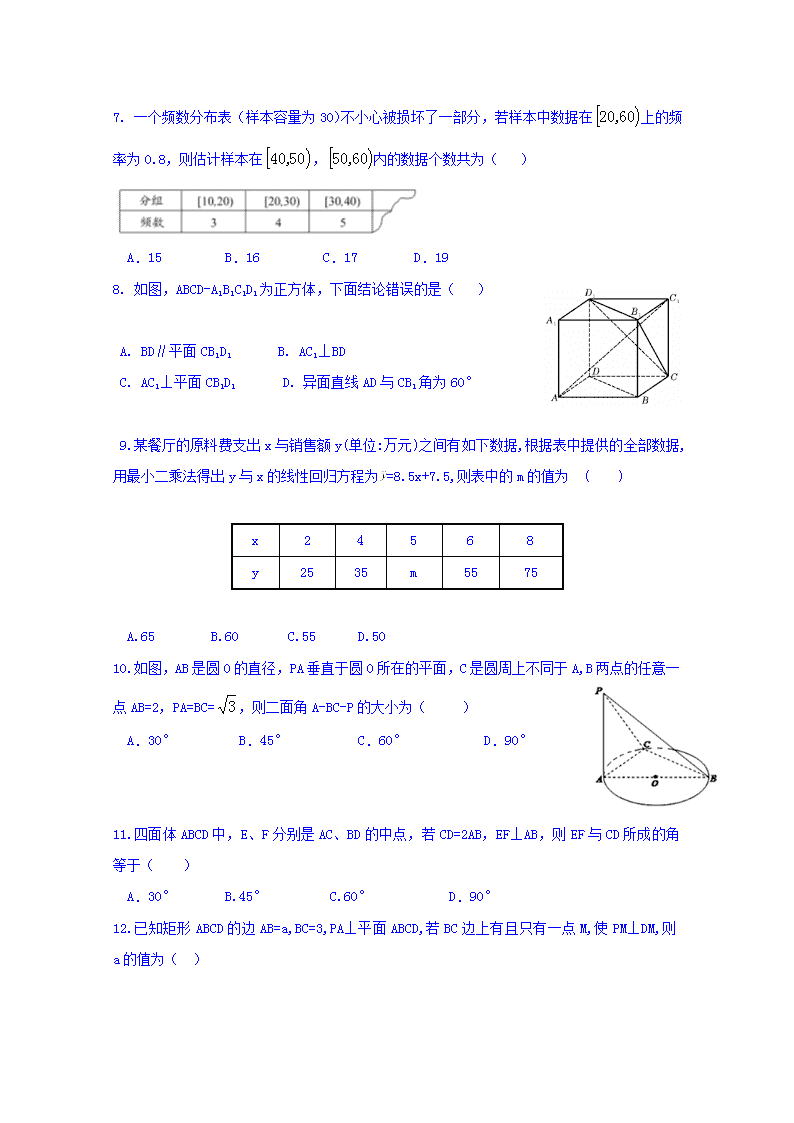
1.某单位有员工120人,其中女员工有72人,为做某项调查,拟采用分层抽样抽取容量为15的样本,则男员工应选取的人数是( )
A. 8 B. 7 C. 6 D. 5
2. 一次选拔运动员,测得7名选手的身高(单位:cm)分布茎叶图如图,记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为( )
A.5 B.6 C.7 D.8
3. 若线性回归方程为=2-3.5x,则当变量x增加一个单位时,变量y ( )
A. 增加2个单位 B. 减少2个单位
C. 增加3.5个单位 D. 减少3.5个单位
4. 设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
A.若α⊥β,m⊂α,n⊂β,则m⊥n B.若m⊥α,m∥n,n∥β,则α⊥β
C.若m⊥n,m⊂α,n⊂β,则α⊥β D.若α∥β,m⊂α,n⊂β,则m∥n
5. 若框图所给的程序运行结果为S=20,那么判断框中应填入的关于k的条件是( )
A. k>8? B. k≥8? C. k<8? D. k≤8?
6.下列说法不正确的是( )
A. 空间中,一组对边平行且相等的四边形一定是平行四边形;
B. 过一条直线有且只有一个平面与已知平面垂直
C. 过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一个平面内;
D. 同一平面的两条垂线一定共面;
7. 一个频数分布表(样本容量为30)不小心被损坏了一部分,若样本中数据在上的频率为0.8,则估计样本在,内的数据个数共为( )
A.15 B.16 C.17 D.19
8. 如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
A. BD∥平面CB1D1 B. AC1⊥BD
C. AC1⊥平面CB1D1 D. 异面直线AD与CB1角为60°
9.某餐厅的原料费支出x与销售额y(单位:万元)之间有如下数据,根据表中提供的全部数据,用最小二乘法得出y与x的线性回归方程为=8.5x+7.5,则表中的m的值为 ( )
x
2
4
5
6
8
y
25
35
m
55
75
A.65 B.60 C.55 D.50
10.如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A,B两点的任意一点AB=2,PA=BC=,则二面角A-BC-P的大小为( )
A.30° B.45° C.60° D.90°
11.四面体ABCD中,E、F分别是AC、BD的中点,若CD=2AB,EF⊥AB,则EF与CD所成的角等于( )
A.30° B.45° C.60° D.90°
12.已知矩形ABCD的边AB=a,BC=3,PA⊥平面ABCD,若BC边上有且只有一点M,使PM⊥DM,则a的值为( )
A. B.1 C. D.2
二、填空题20分(每题5分,共4小题)
13. 某工厂采用系统抽样方法,从一车间全体300名职工中抽取20名职工进行一项安全生产调查,现将300名职工从1到300进行编号,已知从31到45这15个编号中抽到的编号是36,则在1到15中随机抽到的编号应是 .
14. 在三棱柱ABC﹣A1B1C1中,各棱长相等,侧掕垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是 .
15.阅读如图所示的程序框图,若运行该程序后输出的y值为,则输入的实数x值为 .
(第15题) (第16题)
16.(2016·乌鲁木齐模拟)如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD∶BC∶AB=2∶3∶4,点E,F分别是AB,CD的中点,将四边形ADFE沿直线EF进行翻折,给出四个结论:
①DF⊥BC;②BD⊥FC;③平面DBF⊥平面BFC;
④平面DCF⊥平面BFC.
在翻折过程中,可能成立的结论是 .
三、解答题(6道题共70分)
17.(本小题满分10分)某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
(1)若该校高二年级共有学生1000人,试估计成绩不低于60分的人数;
(2)求该校高二年级全体学生期中考试成绩的众数和中位数的估计值.
18.(本小题满分12分)如图,是正方形,是正方形的中心,⊥底面,是的中点
求证:(1)平面;(2)⊥平面.
19.(本小题满分12分)某校高二(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图①②所示,据此解答如下问题:
(1)求高二(1)班全体女生的人数;
(2)求分数在[80,90)之间的女生人数,并计算频率分布直方图中[80,90)之间的矩形的高;
(3)根据频率分布直方图,估计高二(1)班全体女生的数学平均成绩.(同一组中的数据用该组区间的中点值代表)
20.(本小题满分12分)已知某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(1)根据如下的参考公式与参考数据,求利润额y与销售额x之间的线性回归方程;
(2)若该公司还有一个零售店某月销售额为10千万元,试估计它的利润额是多少?
(参考公式:,其中: )
21.(本小题满分12分)
某学校对手工社、摄影社两个社团招新报名的情况进行调查,得到如下的列联表:
(1)请填上上表中所空缺的五个数字;
(2)能否在犯错误的概率不超过0.05的前提下,认为学生对这两个社团的选择与“性别”有关系?
注:
22. (本小题满分12分)已知四棱锥中,且,点分别是中点,平面交.
(1)证明:;
(2)试确定点的位置,并证明你的结论.
红兴隆管理局第一高级中学
2017-2018学年度第一学期高二年级期中考试
数学学科试卷答案
一、选择题:【答案】CDDBA BADBC AC
二、填空题【答案】13. 6 ;14.;15 60°;16.②③
17、【答案】
试题解析:(1)成绩不低于60分所占的频率为:1-(0.004+0.010)10=0.86
所以成绩不低于60分的人数估计值为:10000.86=860(人)
(2)众数估计值:75
设中位数为x,则(x-70)0.032=0.5-0.04-0.1-0.2,解得x=75
18、【答案】
试题解析:证明:(Ⅰ)连接,在中,,
又平面, 平面.
平面.
(Ⅱ)底面,平面,,
又四边形是正方形,,
平面,平面.
19. 【答案】
试题解析:(1)由茎叶图知,分数在[50,60)之间的频数为2,频率分布直方图知,分数在[50,60)之间的频率为0.008×10=0.08,所以全班人数为=25(人).
(2)茎叶图中可见部分共有21人,所以[80,90)之间的女生人数为25-21=4,∴分数在[80,90)之间的频率为=0.16,∴频率分布直方图中[80,90)间的矩形的高为=0.016.
(3)平均成绩为=73.8(分)
20.【答案】
试题解析:(1)由已知数据计算得:
,
则线性回归方程为
(2)将x=10代入线性回归方程中得到(千万元)
21.【答案】
试题解析:(1)
(2)
所以,不能在犯错误的概率不超过0.05的前提下,认为学生对这两个社团的选择与“性别”有关系.
22.【答案】
试题解析:(1)证明
(2)Q是PA的一个四等分点,且.
证明如下:取PE的中点Q,连结MQ,NQ,∵M是PB的中点,∴MQ∥BE,
又∵CN∥BE,∴MQ∥CN,∴Q∈平面MCN,又∵Q∈PA,∴PA∩平面MCN=Q,∴Q是PA的靠近P的一个四等点.