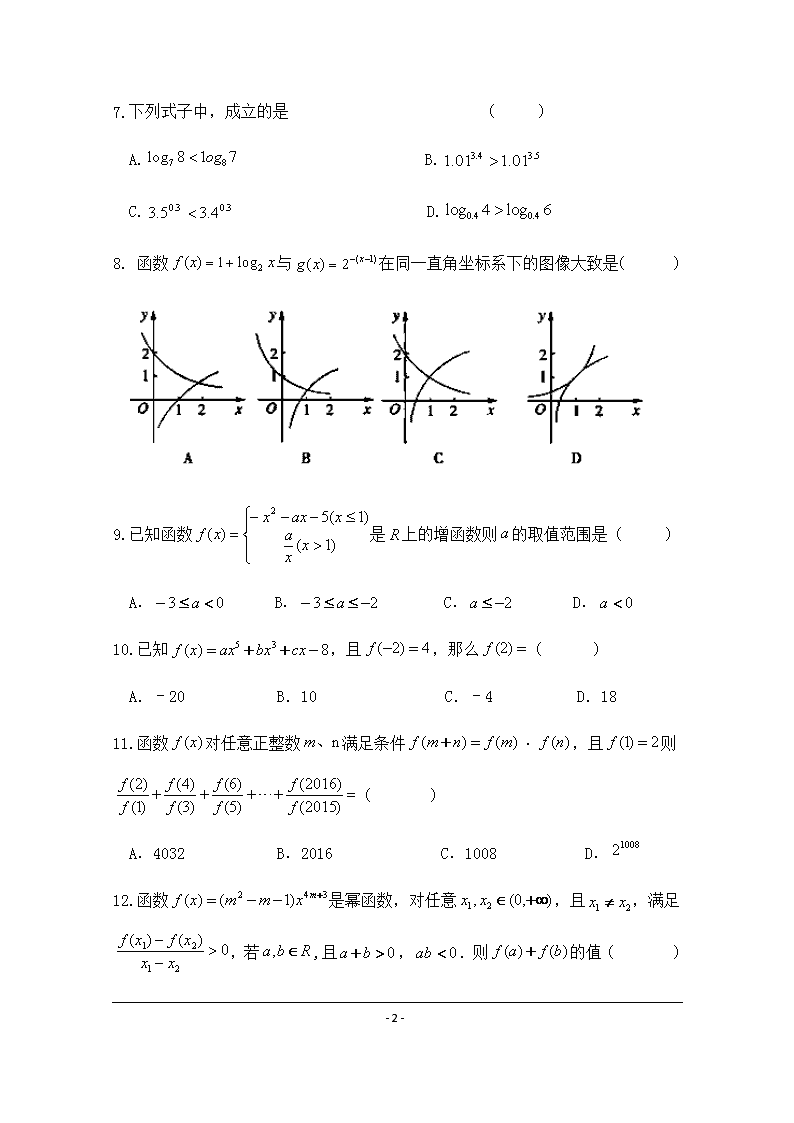江西省信丰中学2019-2020学年高一上学期数学期中复习试卷二 9页

信丰中学高一上学期数学期中复习试卷二 一、选择题（本大题共12小题，每小题5分，共60分）‎ ‎1.已知全集，集合，，则等于( )‎ A．{1,3,5} B．{2,4,6} C．{1,5} D．{1,6}‎ ‎2. 在①；②；③； ④ 上述四个关 系中，错误的个数是（ ） ‎ A. 1个 B. 2个 C. 3个 D. 4个 ‎3. 设集合，则图中阴影 部分表示的集合为( )‎ A． B．‎ C． D．‎ ‎4.与函数是同一个函数的是 ( )‎ A． B． C． D．‎ ‎5.函数在(-∞,+∞)上是减函数，则（ ）‎ ‎ A . B. C. D. ‎ ‎6.已知集合，，则(　 )‎ A． B． C． D．‎ - 9 -‎ ‎7.下列式子中，成立的是 （ ）‎ A. B.‎ C. D.‎ ‎8. 函数与在同一直角坐标系下的图像大致是(　 )‎ ‎9.已知函数是上的增函数则的取值范围是（ 　）‎ A． B． C． D．‎ ‎10.已知，且，那么（　 ）‎ A．﹣20 B．10 C．﹣4 D．18‎ ‎11.函数对任意正整数满足条件·，且则（ 　）‎ A．4032 B．2016 C．1008 D．‎ ‎12.函数是幂函数，对任意，且，满足，若,且，．则的值（　 ）‎ - 9 -‎ A．恒大于0 B．恒小于0 C．等于0 D．无法判断 二、填空题：(本大题4个小题，每小题5分，共20分)‎ ‎13.集合，且，则=　 　． 　‎ ‎14.已知幂函数的图像关于轴对称，且在上单调递减，则 ‎ ‎15.已知全集， ，函数，则函数的值为 ‎ ‎16.下列几个命题：‎ ‎①方程若有一个正实根，一个负实根，则；‎ ‎②函数是偶函数，但不是奇函数；‎ ‎③函数的值域是，则函数的值域为；‎ ‎④ 一条曲线和直线的公共点个数是，‎ 则的值不可能是.‎ 其中正确的有__________.‎ 三、解答题：（本题共6小题,共70分,解答过程应写出文字说明,证明过程或演算步骤）‎ ‎17.（本小题满分10分）已知集合，‎ 求：(1) （2） ‎ - 9 -‎ 18. ‎（本小题满分12分）（1）计算：；‎ ‎（2）解方程：‎ ‎19.（本小题满分12分）已知函数.‎ ‎（1）设,函数的定义域为, 求的最大值;‎ ‎（2）当时，求使的的取值范围.‎ ‎20.（本小题满分12分）乒乓球是我国的国球，在2016年巴西奥运会上尽领风骚，包揽该项目全部金牌，现某市有甲、乙两家乒乓球俱乐部，两家设备和服务都很好，但收费方式不同，甲家每张球台每小时元;乙家按月计费，一个月中小时以内（含小时）每张球台元，超过小时的部分，每张球台每小时元，某公司准备下个月从这两家中的一家租一张球台开展活动，其活动时间不少于小时，也不超过小时.‎ ‎（1）设在甲家租一张球台开展活动小时的收费为 元,在乙家租一张球台开展活动小时的收费为元,试求与的解析式.‎ ‎（2）选择哪家比较合算？为什么？ ‎ ‎21.(本小题满分12分) 已知函数 ， ‎ ‎（1）若，求在区间上的最小值；‎ - 9 -‎ ‎（2）若在区间上有最大值，求实数的值 ‎22．(本小题满分12分)设函数是定义域为R的奇函数．‎ ‎（1）若，试求不等式的解集；‎ ‎（2）若，且，求g(x)在[1，＋∞)上的最小值.‎ - 9 -‎ 高一数学期中复习卷二参考答案 一、 DBBCA CDCBA BA 二、 ‎13. 14.1 15. 0,-4 16.①④ ‎ 三、17．解　(1) ……………2分 ‎ ……………5分 ‎(2) ……………7分 ‎ ……………10分 ‎18.解：（1）原式＝＋(lg 5)0＋＝＋1＋＝4. ………6分 ‎（2）由方程log3(6x－9)＝3得 ‎6x－9＝33＝27，∴6x＝36＝62， ‎ ‎∴x＝2. 经检验，x＝2是原方程的解． ……………12分 19. 解：（1）当时，,在为减函数，‎ 因此当时最大值为 ……………5分 （2） ‎,即当时，,满足,故当时解集为:.……12分 ‎20.解：（1） ； .…………6分 - 9 -‎ ‎（2） ①当时，,即当时,;当时,,当时,.‎ ‎②当时,,‎ 综上 当时,选甲家比较合算; 当时,两家一样合算;‎ 当时,选乙家比较合算. ……………12分 ‎21解：（1）若，则 ‎ 函数图像开口向下，对称轴为，‎ ‎ 所以函数在区间上是增加的，在区间上是减少的，‎ 有又， …………3分 ‎（2）对称轴为 当时，函数在在区间上是减少的，则 ‎ ，即；…………6分 当时，函数在区间上是增加的，在区间上是减少加的，则 ‎，解得，不符合；…………9分 当时，函数在区间上是增加的，则 ‎，解得； …………11分 综上所述，或 …………12分 ‎22. 解：∵f(x)是定义域为R的奇函数，‎ ‎∴f(0)＝0，∴k－1＝0，∴k＝1 .……………1分 - 9 -‎ ‎(1)∵f (1)>0，∴a－>0. 又a>0且a≠1，∴a>1.‎ ‎∵k＝1，∴f(x)＝ax－a－x.‎ 当a>1时，y＝ax和y＝－a－x在R上均为增函数，‎ ‎∴f(x)在R上为增函数． ……………3分 原不等式可化为f (x2＋2x)>f(4－x)，‎ ‎∴x2＋2x>4－x，即x2＋3x－4>0.‎ ‎∴x>1或x<－4.‎ ‎∴不等式的解集为{x|x>1或x<－4}． ……………6分 ‎(2)∵f(1)＝，∴a－＝，即2a2－3a－2＝0.‎ ‎∴a＝2或a＝－(舍去)． ……………7分 ‎∴g(x)＝22x＋2－2x－4(2x－2－x)＝(2x－2－x)2－4(2x－2－x)＋2.‎ 令t＝h(x)＝2x－2－x(x≥1)，‎ 则g(t)＝t2－4t＋2.‎ ‎∵t＝h(x)在[1，＋∞)上为增函数(由(1)可知)，‎ ‎∴h(x)≥h(1)＝，即t≥.‎ ‎∵g(t)＝t2－4t＋2＝(t－2)2－2，t∈[，＋∞)，……………10分 ‎∴当t＝2时，g(t)取得最小值－2，即g(x)取得最小值－2，‎ 此时x＝log2(1＋)．‎ 故当x＝log2(1＋)时，g(x)有最小值－2.……………12分 - 9 -‎ - 9 -‎