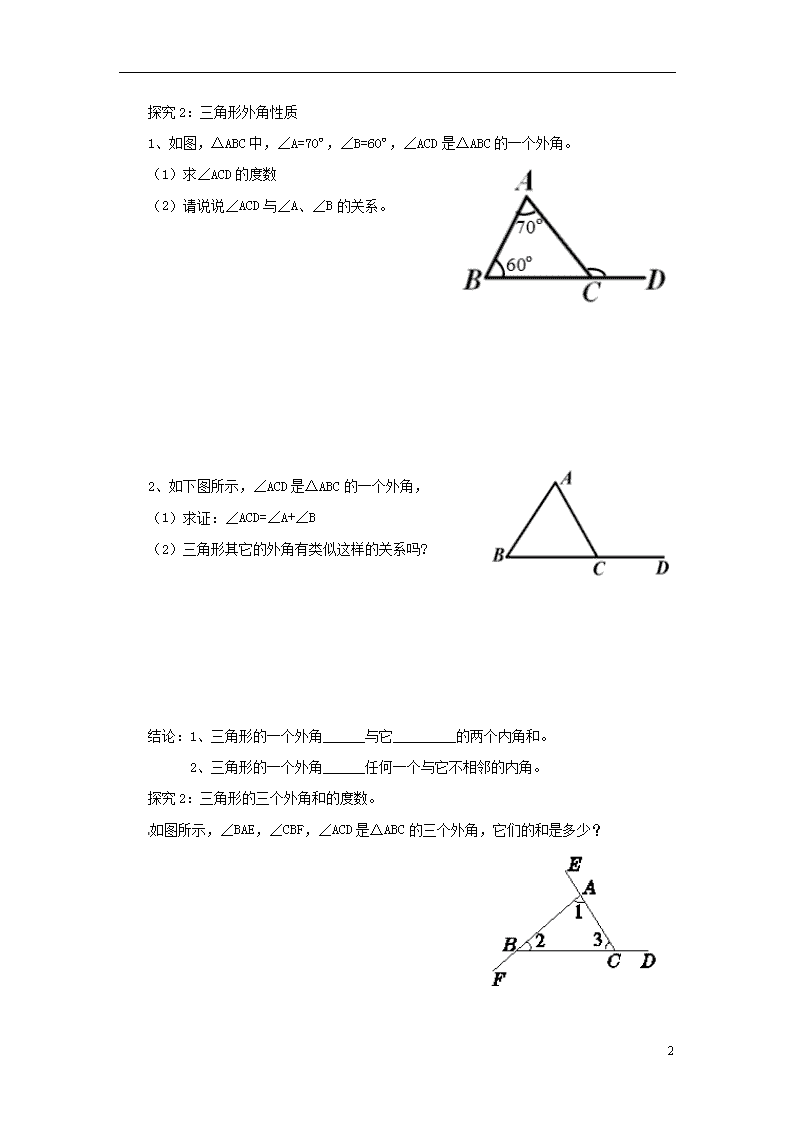2020八年级数学上册 第11章 三角形 11.2.2 三角形的外角 4页

课题：‎11.2.2‎ 三角形的外角 ‎【学习目标】‎ ‎1、了解三角形外角的概念；‎ ‎2、探索并证明三角形的一个外角等于与它不相邻的两个内角和；‎ ‎3、运用三角形的一个外角大于与它不相邻的任何一个内角解决简单的实际问题。‎ ‎【学习重点】‎ ‎1、了解三角形外角的概念及性质；‎ ‎2、能利用三角外角的性质解决简单的实际问题。‎ ‎【学习难点】‎ ‎1、能够证明“三角形的一个外角等于与它不相邻的两个内角和”；‎ ‎2、了解“三角形的一个外角大于与它不相邻的任何一个内角”的应用范围，并能解决简单的实际问题。‎ ‎【学习过程】‎ ‎※ 自主学习 ‎1、阅读教材第14至第16页，用红笔对有关概念进行勾画并完成下列问题。‎ ‎2、找出自己的疑惑和要讨论的问题，准备在课堂上讨论质疑 ‎※ 合作与探究 探究1：三角形的外角的定义 ‎ 观察下列图，∠ACD的顶点与两边有什么特征，这样的角如何称呼？‎ 探究结论：________________________________________________‎ ‎__________________________________________________________‎ ‎__________________________________________________________‎ 4‎ 探究2：三角形外角性质 1、 如图，△ABC中，∠A=70º，∠B=60º，∠ACD是△ABC的一个外角。‎ （1） 求∠ACD的度数 （2） 请说说∠ACD与∠A、∠B的关系。‎ 2、 如下图所示，∠ACD是△ABC的一个外角，‎ ‎（1）求证：∠ACD=∠A+∠B ‎（2）三角形其它的外角有类似这样的关系吗?‎ 结论：1、三角形的一个外角______与它_________的两个内角和。‎ ‎2、三角形的一个外角______任何一个与它不相邻的内角。‎ 探究2：三角形的三个外角和的度数。‎ 如图所示，∠BAE，∠CBF，∠ACD是△ABC的三个外角，它们的和是多少？‎ 4‎ 结论：三角形的三个外角和是______度。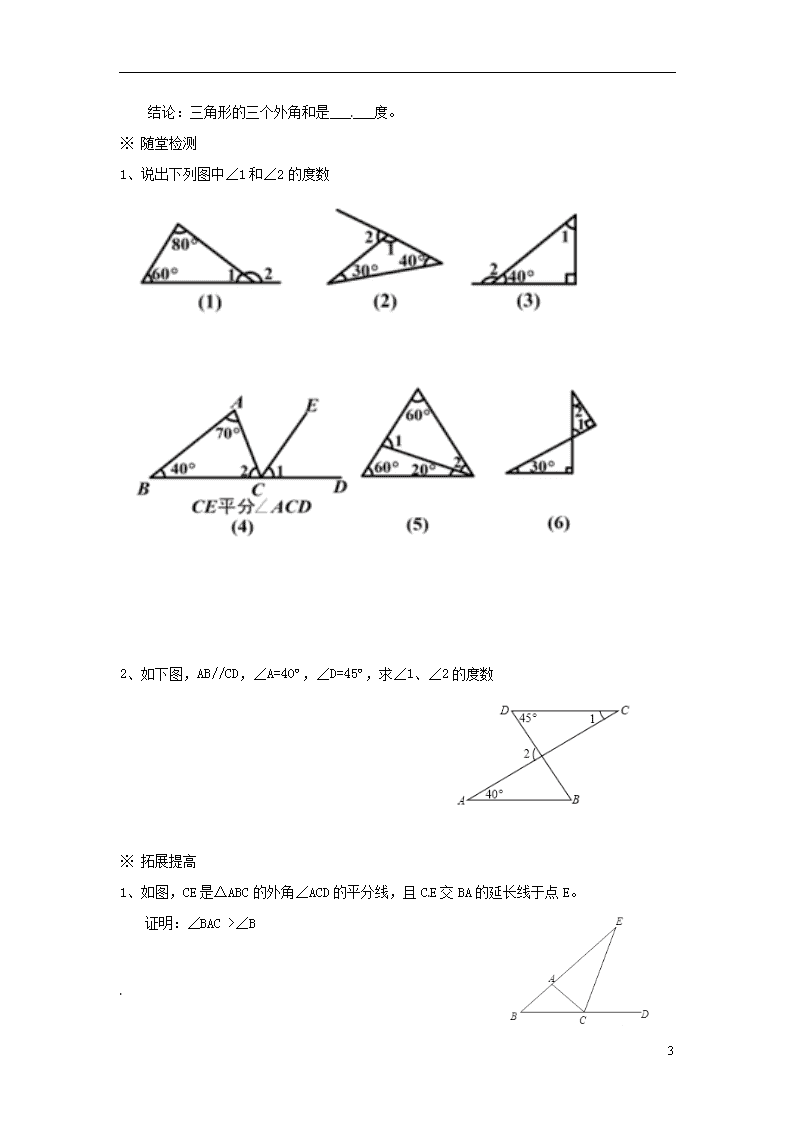‎ ‎※ 随堂检测 1、 说出下列图中∠1和∠2的度数 2、 如下图，AB//CD，∠A=40º，∠D=45º，求∠1、∠2的度数 ‎※ 拓展提高 ‎1、如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E。‎ 证明：∠BAC >∠B 4‎ ‎2、如下图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E。‎ 求证：∠BAC =∠B+2∠E 1、 如下图，在△ABC中，∠ABC与∠ACB的平分线交于点P，‎ ‎ 试证明:∠P=90º+ ∠A 教（学）后反思：_______________________________________________________________‎ ‎_____________________________________________________________________ （实际使用课时 ______节）‎ 4‎